Neutrino oscillation
Encyclopedia
Neutrino oscillation is a quantum mechanical
phenomenon predicted by Bruno Pontecorvo
whereby a neutrino
created with a specific lepton
flavor (electron
, muon
or tau
) can later be measured to have a different flavor. The probability of measuring a particular flavor for a neutrino varies periodically as it propagates. Neutrino oscillation is of theoretical
and experimental
interest since observation of the phenomenon implies that the neutrino has a non-zero mass, which is not part of the original Standard Model
of particle physics
.
Homestake Experiment
in the late 1960s, in which he observed a deficit in the flux of solar
neutrinos with respect to the prediction of the Standard Solar Model
, using a chlorine
-based detector. This gave rise to the Solar neutrino problem
. Many subsequent radiochemical and water Cherenkov
detectors confirmed the deficit, but neutrino oscillation was not conclusively identified as the source of the deficit until the Sudbury Neutrino Observatory
provided clear evidence of neutrino flavor change in 2001.
Solar neutrinos have energies below 20 MeV
and travel an astronomical unit
between the source in the Sun and detector on the Earth. At energies above 5 MeV, solar neutrino oscillation actually takes place in the Sun through a resonance known as the MSW effect, a different process from the vacuum oscillation described later in this article.
, MACRO
, and Kamiokande II observed a deficit in the ratio of the flux of muon to electron flavor atmospheric neutrinos (see muon decay). The Super Kamiokande experiment provided a very precise measurement of neutrino oscillation in an energy range of hundreds of MeV to a few TeV, and with a baseline of the diameter of the Earth
.
-neutrinos produced at nuclear reactors. A high precision observation of reactor neutrino oscillation has been made by the KamLAND experiment since 2002. Neutrinos produced in nuclear reactors have energies similar to solar neutrinos, a few MeV. The baselines of these experiments have ranged from tens of meters to over 100 km.
offer the greatest control over the neutrinos being studied. Many experiments have taken place which study the same neutrino oscillations which take place in atmospheric neutrino oscillation, using neutrinos with a few GeV of energy and several hundred km baselines. The MINOS
experiment recently announced that it observes consistency with the results of the K2K
and Super-K
experiments.
The controversial observation of beam neutrino oscillation at the LSND experiment in 2006 was tested by MiniBooNE
. Results from MiniBooNE appeared in Spring 2007, and appeared to contradict the findings of the LSND experiment.
On 31 May 2010, the INFN and CERN
announced having observed a tau particle in a muon neutrino beam in the OPERA detector
located at Gran Sasso
, 730 km away from the neutrino source in Geneva
.
The upcoming T2K experiment will direct a neutrino beam through 295 km of earth, and will measure the parameter θ13. The experiment is scheduled to begin in 2009 and uses the Super-K detector. NOνA is a similar effort. This detector will use the same beam as MINOS and will have a baseline of 810 km.
of the three neutrino states of definite mass. Neutrinos are created in weak
decays and reactions in their flavor eigenstates. As a neutrino propagates through space, the quantum mechanical phases
of the three mass states advance at slightly different rates due to the slight differences in the neutrino masses. This results in a changing mixture of mass states as the neutrino travels, but a different mixture of mass states corresponds to a different mixture of flavor states. So a neutrino born as, say, an electron neutrino will be some mixture of electron, mu, and tau neutrino after traveling some distance. Since the quantum mechanical phase advances in a periodic fashion, after some distance the state will nearly return to the original mixture, and the neutrino will be again mostly electron neutrino. The electron flavor content of the neutrino will then continue to oscillate as long as the quantum mechanical state maintains coherence. It is because the mass differences between the neutrinos are small that the coherence length
for neutrino oscillation is so long, making this microscopic quantum effect observable over macroscopic distances.
, who proposed that neutrino-antineutrino transitions may occur in analogy with neutral kaon mixing. Although such matter-antimatter oscillation has not been observed, this idea formed the conceptual foundation for the quantitative theory of neutrino flavor oscillation, which was first developed by Maki, Nakagawa, and Sakata in 1962
and further elaborated by Pontecorvo in 1967. One year later the solar neutrino deficit was first observed, and that was followed by the famous paper of Gribov and Pontecorvo published in 1969 titled "Neutrino astronomy and lepton charge".
The unitary transformation relating the flavor and mass eigenbases can be written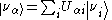
,
where
represents the Pontecorvo–Maki–Nakagawa–Sakata matrix (also called the PMNS matrix, lepton mixing matrix, or sometimes simply the MNS matrix). It is the analogue of the CKM matrix describing the analogous mixing of quark
s. If this matrix were the identity matrix
, then the flavor eigenstates would be the same as the mass eigenstates. However, experiment shows that it is not.
When the standard three neutrino theory is considered, the matrix is 3×3. If only two neutrinos are considered, a 2×2 matrix is used. If one or more sterile neutrinos are added (see later) it is 4×4 or larger. In the 3×3 form, it is given by:
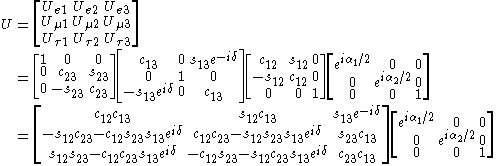
where cij = cosθij and sij = sinθij. The phase factors α1 and α2 are physically meaningful only if neutrinos are Majorana particles — i.e. if the neutrino is identical to its antineutrino (whether or not they are is unknown) — and do not enter into oscillation phenomena regardless. If neutrinoless double beta decay occurs, these factors influence its rate. The phase factor δ is non-zero only if neutrino oscillation violates CP symmetry. This is expected, but not yet observed experimentally. If experiment shows this 3×3 matrix to be not unitary, a sterile neutrino
or some other new physics is required.
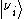are mass eigenstates, their propagation can be described by plane wave
solutions of the form
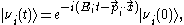
where
In the ultrarelativistic limit
,
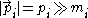, we can approximate the energy as
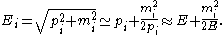
This limit applies to all practical (currently observed) neutrinos, since their masses are less than 1 eV and their energies are at least 1 MeV, so the Lorentz factor
γ is greater than 106 in all cases. Using also t ≈ L, where L is the distance traveled and also dropping the phase factors, the wavefunction becomes:
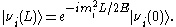
Eigenstates with different masses propagate at different speeds. The heavier ones lag behind while the lighter ones pull ahead. Since the mass eigenstates are combinations of flavor eigenstates, this difference in speed causes interference between the corresponding flavor components of each mass eigenstate. Constructive interference
causes it to be possible to observe a neutrino created with a given flavor to change its flavor during its propagation. The probability that a neutrino originally of flavor α will later be observed as having flavor β is
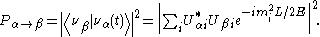
This is more conveniently written as
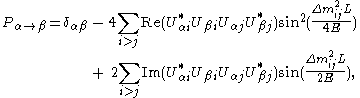
where
. The phase that is responsible for oscillation is often written as (with c and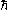 
restored)
where 1.267 is unitless. In this form, it is convenient to plug in the oscillation parameters since:
If there is no CP-violation (δ is zero), then the second sum is zero.
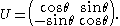
Then the probability of a neutrino changing its flavor is
Or, using SI units and the convention introduced above
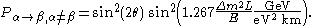
This formula is often appropriate for discussing the transition νμ ↔ ντ in atmospheric mixing, since the electron neutrino plays almost no role in this case. It is also appropriate for the solar case of νe ↔ νx, where νx is a superposition of νμ and ντ. These approximations are possible because the mixing angle θ13 is very small and because two of the mass states are very close in mass compared to the third.
s. A simple example is a system of two pendulum
s connected by a weak spring (a spring with a small spring constant). The first pendulum is set in motion by the experimenter while the second begins at rest. Over time, the second pendulum begins to swing under the influence of the spring, while the first pendulum's amplitude decreases as it loses energy to the second. Eventually all of the system's energy is transferred to the second pendulum and the first is at rest. The process then reverses. The energy oscillates between the two pendulums repeatedly until it is lost to friction
.
The behavior of this system can be understood by looking at its normal modes of oscillation. If the two pendulums are identical then one normal mode consists of both pendulums swinging in the same direction with a constant distance between them, while the other consists of the pendulums swinging in opposite (mirror image) directions. These normal modes have (slightly) different frequencies because the second involves the (weak) spring while the first does not. The initial state of the two-pendulum system is a combination of both normal modes. Over time, these normal modes drift out of phase, and this is seen as a transfer of motion from the first pendulum to the second.
When the pendulums are not identical the analysis is slightly more complicated. In the small-angle approximation, the potential energy
of a single pendulum system is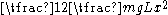
, where g is the standard gravity
, L is the length of the pendulum, m is the mass of the pendulum bob, and x is the horizontal displacement of the pendulum bob. As an isolated system the pendulum is a harmonic oscillator with a frequency of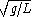
. The potential energy of a spring is 
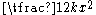where k is the spring constant and x is the displacement. With a mass attached it oscillates with a period of 
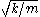. With two pendulums (labeled a and b) of equal mass but possibly unequal lengths and connected by a spring, the total potential energy is
This is a quadratic form
in xa and xb, which can also be written as a matrix product:
The 2×2 matrix is real symmetric and so (by the spectral theorem
) it is "orthogonally
diagonalizable
". That is, there is an angle θ such that if we define
then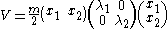
where λ1 and λ2 are the eigenvalues of the matrix. The variables x1 and x2 describe normal modes which oscillate with frequencies of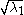
and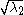 
. When the two pendulums are identical (La = Lb), θ is 45°.
The description of the system in terms of the two pendulums (a and b) is analogous to the flavor basis of neutrinos. These are the parameters that are most easily produced and detected (in the case of neutrinos, by weak interactions involving the W boson). The description in terms of normal modes is analogous to the mass basis of neutrinos. These modes do not interact with each other when the system is free of outside influence. The angle θ is analogous to the Cabibbo angle (though that angle applies to quarks rather than neutrinos).
When the number of oscillators (particles) is increased to three, the orthogonal matrix can no longer be described by a single angle; instead, three are required (Euler angles
). Furthermore, in the quantum case, the matrices may be complex
. This requires the introduction of complex phases in addition to the rotation angles, which are associated with CP violation
but do not influence the observable effects of neutrino oscillation.
The blue curve shows the probability of the original neutrino retaining its identity. The red curve shows the probability of conversion to the other neutrino. The maximum probability of conversion is equal to sin22θ. The frequency of the oscillation is controlled by Δm2.
Solar neutrino experiments combined with KamLAND
have measured the so-called solar parameters Δm and sin2θsol. Atmospheric neutrino experiments such as Super-Kamiokande
together with the K2K and MINOS long baseline accelerator neutrino experiment have determined the so-called atmospheric parameters Δm and sin2θatm.
For atmospheric neutrinos (where the relevant difference of masses is about and the typical energies are ), oscillations become visible for neutrinos traveling several hundred km, which means neutrinos that reach the detector from below the horizon.
From atmospheric and solar neutrino
oscillation experiments, it is known that two mixing angles of the MNS matrix are large and the third is smaller. This is in sharp contrast to the CKM matrix in which all three angles are small and hierarchically decreasing. Nothing is known about the CP-violating phase of the MNS matrix.
If the neutrino mass proves to be of Majorana
type (making the neutrino its own antiparticle), it is possible that the MNS matrix has more than one phase.
Since experiments observing neutrino oscillation measure the squared mass difference and not absolute mass, one can claim that the lightest neutrino mass is exactly zero, without contradicting observations. This is however regarded as unlikely by theorists.
s only have mass because of interactions with the Higgs field (see Higgs boson
). These interactions involve both left- and right-handed versions of the fermion (see chirality
). However, only left-handed neutrinos have been observed so far.
Neutrinos may have another source of mass through the Majorana
mass term. This type of mass applies for electrically-neutral particles since otherwise it would allow particles to turn into anti-particles, which would violate conservation of electric charge.
The smallest modification to the Standard Model, which only has left-handed neutrinos, is to allow these left-handed neutrinos to have Majorana masses. The problem with this is that the neutrino masses are implausibly smaller than the rest of the known particles (at least 500,000 times smaller than the mass of an electron), which, while it does not invalidate the theory, is not very satisfactory.
The next simplest addition would be to add right-handed neutrinos into the Standard Model, which interact with the left-handed neutrinos and the Higgs field in an analogous way to the rest of the fermions. These new neutrinos would interact with the other fermions solely in this way, so are not phenomenologically excluded. The problem of the disparity of the mass scales remains.
If it is assumed that the neutrinos interact with the Higgs field with approximately the same strengths as the charged fermions do, the heavy mass should be close to the GUT scale. Note that, in the Standard Model there is just one fundamental mass scale (which can be taken as the scale of breaking) and all masses (such as the electron or the mass of the Z boson) have to originate from this one.
There are other varieties of seesaw and currently it is not clear which, if any, nature has chosen.
The apparently innocent addition of right-handed neutrinos has the effect of adding new mass scales, completely unrelated to the mass scale of the Standard Model. Thus, heavy right-handed neutrinos look to be the first real glimpse of physics beyond the Standard Model. It is interesting to note that right-handed neutrinos can help to explain the origin of matter through a mechanism known as leptogenesis
.
if they are all included. These models have little predictive power and are not able to provide a cold dark matter candidate but they are considered interesting since they would be compatible with new observable signals in particle colliders.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
phenomenon predicted by Bruno Pontecorvo
Bruno Pontecorvo
Bruno Pontecorvo was an Italian-born nuclear physicist, an early assistant of Enrico Fermi and then the author of numerous studies in high energy physics, especially on neutrinos. According to Oleg Gordievsky and Pavel Sudoplatov , Pontecorvo was also a Soviet agent...
whereby a neutrino
Neutrino
A neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...
created with a specific lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
flavor (electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
, muon
Muon
The muon |mu]] used to represent it) is an elementary particle similar to the electron, with a unitary negative electric charge and a spin of ½. Together with the electron, the tau, and the three neutrinos, it is classified as a lepton...
or tau
Tau lepton
The tau , also called the tau lepton, tau particle or tauon, is an elementary particle similar to the electron, with negative electric charge and a spin of . Together with the electron, the muon, and the three neutrinos, it is classified as a lepton...
) can later be measured to have a different flavor. The probability of measuring a particular flavor for a neutrino varies periodically as it propagates. Neutrino oscillation is of theoretical
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
and experimental
Experimental physics
Within the field of physics, experimental physics is the category of disciplines and sub-disciplines concerned with the observation of physical phenomena in order to gather data about the universe...
interest since observation of the phenomenon implies that the neutrino has a non-zero mass, which is not part of the original Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
.
Observations
A great deal of evidence for neutrino oscillation has been collected from many sources, over a wide range of neutrino energies and with many different detector technologies.Solar neutrino oscillation
The first experiment to detect the effects of neutrino oscillation was Ray Davis'sRaymond Davis Jr.
Raymond Davis, Jr. was an American chemist, physicist, and Nobel Prize in Physics laureate.-Early life and education:...
Homestake Experiment
Homestake Experiment
The Homestake experiment was an experiment headed by astrophysicists Raymond Davis, Jr. and John N. Bahcall in the late 1960s. Its purpose was to collect and count neutrinos emitted by nuclear fusion taking place in the Sun. Bahcall did the theoretical calculations and Davis designed the experiment...
in the late 1960s, in which he observed a deficit in the flux of solar
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
neutrinos with respect to the prediction of the Standard Solar Model
Standard Solar Model
The Standard Solar Model refers to a mathematical treatment of the Sun as a spherical ball of gas...
, using a chlorine
Chlorine
Chlorine is the chemical element with atomic number 17 and symbol Cl. It is the second lightest halogen, found in the periodic table in group 17. The element forms diatomic molecules under standard conditions, called dichlorine...
-based detector. This gave rise to the Solar neutrino problem
Solar neutrino problem
The solar neutrino problem was a major discrepancy between measurements of the numbers of neutrinos flowing through the Earth and theoretical models of the solar interior, lasting from the mid-1960s to about 2002...
. Many subsequent radiochemical and water Cherenkov
Cherenkov radiation
Cherenkov radiation is electromagnetic radiation emitted when a charged particle passes through a dielectric medium at a speed greater than the phase velocity of light in that medium...
detectors confirmed the deficit, but neutrino oscillation was not conclusively identified as the source of the deficit until the Sudbury Neutrino Observatory
Sudbury Neutrino Observatory
The Sudbury Neutrino Observatory is a neutrino observatory located 6,800 feet underground in Vale Inco's Creighton Mine in Sudbury, Ontario, Canada. The detector was designed to detect solar neutrinos through their interactions with a large tank of heavy water. The detector turned on in May 1999,...
provided clear evidence of neutrino flavor change in 2001.
Solar neutrinos have energies below 20 MeV
MEV
MeV and meV are multiples and submultiples of the electron volt unit referring to 1,000,000 eV and 0.001 eV, respectively.Mev or MEV may refer to:In entertainment:* Musica Elettronica Viva, an Italian musical group...
and travel an astronomical unit
Astronomical unit
An astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....
between the source in the Sun and detector on the Earth. At energies above 5 MeV, solar neutrino oscillation actually takes place in the Sun through a resonance known as the MSW effect, a different process from the vacuum oscillation described later in this article.
Atmospheric neutrino oscillation
Large detectors such as IMBIrvine-Michigan-Brookhaven (detector)
IMB, the Irvine-Michigan-Brookhaven detector, was a nucleon decay experiment and neutrino observatory located in a Morton Salt company's Fairport mine on the shore of Lake Erie in the United States. It was a joint venture of the University of California, Irvine, the University of Michigan, and...
, MACRO
Monopole, Astrophysics and Cosmic Ray Observatory
MACRO, or the Monopole, Astrophysics and Cosmic Ray Observatory, is a particle physics experiment located at the Laboratori Nazionali del Gran Sasso in Abruzzo, Italy. A number of universities contributed personnel and equipment, including Boston University and University of L'Aquila.The primary...
, and Kamiokande II observed a deficit in the ratio of the flux of muon to electron flavor atmospheric neutrinos (see muon decay). The Super Kamiokande experiment provided a very precise measurement of neutrino oscillation in an energy range of hundreds of MeV to a few TeV, and with a baseline of the diameter of the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
.
Reactor neutrino oscillation
Many experiments have searched for oscillation of electron antiAntimatter
In particle physics, antimatter is the extension of the concept of the antiparticle to matter, where antimatter is composed of antiparticles in the same way that normal matter is composed of particles...
-neutrinos produced at nuclear reactors. A high precision observation of reactor neutrino oscillation has been made by the KamLAND experiment since 2002. Neutrinos produced in nuclear reactors have energies similar to solar neutrinos, a few MeV. The baselines of these experiments have ranged from tens of meters to over 100 km.
Beam neutrino oscillation
Neutrino beams produced at a particle acceleratorParticle accelerator
A particle accelerator is a device that uses electromagnetic fields to propel charged particles to high speeds and to contain them in well-defined beams. An ordinary CRT television set is a simple form of accelerator. There are two basic types: electrostatic and oscillating field accelerators.In...
offer the greatest control over the neutrinos being studied. Many experiments have taken place which study the same neutrino oscillations which take place in atmospheric neutrino oscillation, using neutrinos with a few GeV of energy and several hundred km baselines. The MINOS
MINOS
MINOS is a particle physics experiment designed to study the phenomena of neutrino oscillations, first discovered by a Super-Kamiokande experiment in 1998...
experiment recently announced that it observes consistency with the results of the K2K
K2K experiment
The K2K experiment was a neutrino experiment that ran from June 1999 to November 2004. It used muon neutrinos from a well-controlled and well-understood beam to verify the oscillations previously observed by Super-Kamiokande using atmospheric neutrinos...
and Super-K
Super-Kamiokande
Super-Kamiokande is a neutrino observatory which is under Mount Kamioka near the city of Hida, Gifu Prefecture, Japan...
experiments.
The controversial observation of beam neutrino oscillation at the LSND experiment in 2006 was tested by MiniBooNE
MiniBooNE
MiniBooNE is an experiment at Fermilab designed to observe neutrino oscillations . A neutrino beam consisting primarily of muon neutrinos is directed at a detector filled with 800 tons of mineral oil and lined with 1,280 photomultiplier tubes...
. Results from MiniBooNE appeared in Spring 2007, and appeared to contradict the findings of the LSND experiment.
On 31 May 2010, the INFN and CERN
CERN
The European Organization for Nuclear Research , known as CERN , is an international organization whose purpose is to operate the world's largest particle physics laboratory, which is situated in the northwest suburbs of Geneva on the Franco–Swiss border...
announced having observed a tau particle in a muon neutrino beam in the OPERA detector
OPERA Experiment
The Oscillation Project with Emulsion-tRacking Apparatus is a scientific experiment for detecting tau neutrinos from muon neutrino oscillations. It is a collaboration between CERN in Geneva, Switzerland, and the Laboratori Nazionali del Gran Sasso in Gran Sasso, Italy and uses the CERN Neutrinos...
located at Gran Sasso
Laboratori Nazionali del Gran Sasso
Laboratori Nazionali del Gran Sasso is a particle physics laboratory of the INFN, situated near the Gran Sasso mountain in Italy, between the towns of L'Aquila and Teramo, about 120 km from Rome. In addition to a surface portion of the laboratory, there are extensive underground facilities...
, 730 km away from the neutrino source in Geneva
Geneva
Geneva In the national languages of Switzerland the city is known as Genf , Ginevra and Genevra is the second-most-populous city in Switzerland and is the most populous city of Romandie, the French-speaking part of Switzerland...
.
The upcoming T2K experiment will direct a neutrino beam through 295 km of earth, and will measure the parameter θ13. The experiment is scheduled to begin in 2009 and uses the Super-K detector. NOνA is a similar effort. This detector will use the same beam as MINOS and will have a baseline of 810 km.
Theory
Neutrino oscillation arises from a mixture between the flavor and mass eigenstates of neutrinos. That is, the three neutrino states that interact with the charged leptons in weak interactions are each a different superpositionQuantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of the three neutrino states of definite mass. Neutrinos are created in weak
Weak interaction
Weak interaction , is one of the four fundamental forces of nature, alongside the strong nuclear force, electromagnetism, and gravity. It is responsible for the radioactive decay of subatomic particles and initiates the process known as hydrogen fusion in stars...
decays and reactions in their flavor eigenstates. As a neutrino propagates through space, the quantum mechanical phases
Phase factor
For any complex number written in polar form , the phase factor is the exponential part, i.e. eiθ. As such, the term "phase factor" is similar to the term phasor, although the former term is more common in quantum mechanics. This phase factor is itself a complex number of absolute value 1...
of the three mass states advance at slightly different rates due to the slight differences in the neutrino masses. This results in a changing mixture of mass states as the neutrino travels, but a different mixture of mass states corresponds to a different mixture of flavor states. So a neutrino born as, say, an electron neutrino will be some mixture of electron, mu, and tau neutrino after traveling some distance. Since the quantum mechanical phase advances in a periodic fashion, after some distance the state will nearly return to the original mixture, and the neutrino will be again mostly electron neutrino. The electron flavor content of the neutrino will then continue to oscillate as long as the quantum mechanical state maintains coherence. It is because the mass differences between the neutrinos are small that the coherence length
Coherence length
In physics, coherence length is the propagation distance from a coherent source to a point where an electromagnetic wave maintains a specified degree of coherence. The significance is that interference will be strong within a coherence length of the source, but not beyond it...
for neutrino oscillation is so long, making this microscopic quantum effect observable over macroscopic distances.
Pontecorvo–Maki–Nakagawa–Sakata matrix
The idea of neutrino oscillation was first put forward in 1957 by Bruno PontecorvoBruno Pontecorvo
Bruno Pontecorvo was an Italian-born nuclear physicist, an early assistant of Enrico Fermi and then the author of numerous studies in high energy physics, especially on neutrinos. According to Oleg Gordievsky and Pavel Sudoplatov , Pontecorvo was also a Soviet agent...
, who proposed that neutrino-antineutrino transitions may occur in analogy with neutral kaon mixing. Although such matter-antimatter oscillation has not been observed, this idea formed the conceptual foundation for the quantitative theory of neutrino flavor oscillation, which was first developed by Maki, Nakagawa, and Sakata in 1962
and further elaborated by Pontecorvo in 1967. One year later the solar neutrino deficit was first observed, and that was followed by the famous paper of Gribov and Pontecorvo published in 1969 titled "Neutrino astronomy and lepton charge".
The unitary transformation relating the flavor and mass eigenbases can be written
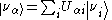
,where
-
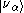is a neutrino with definite flavor. α = e (electron), μ (muon) or τ (tauon). -
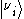is a neutrino with definite mass 
, 
1, 2, 3. - The asterisk (
) represents a complex conjugateComplex conjugateIn mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
. For antineutrinos, the complex conjugate should be dropped from the second equation, and added to the first.
represents the Pontecorvo–Maki–Nakagawa–Sakata matrix (also called the PMNS matrix, lepton mixing matrix, or sometimes simply the MNS matrix). It is the analogue of the CKM matrix describing the analogous mixing of quarkQuark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s. If this matrix were the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, then the flavor eigenstates would be the same as the mass eigenstates. However, experiment shows that it is not.
When the standard three neutrino theory is considered, the matrix is 3×3. If only two neutrinos are considered, a 2×2 matrix is used. If one or more sterile neutrinos are added (see later) it is 4×4 or larger. In the 3×3 form, it is given by:
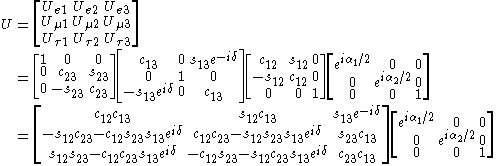
where cij = cosθij and sij = sinθij. The phase factors α1 and α2 are physically meaningful only if neutrinos are Majorana particles — i.e. if the neutrino is identical to its antineutrino (whether or not they are is unknown) — and do not enter into oscillation phenomena regardless. If neutrinoless double beta decay occurs, these factors influence its rate. The phase factor δ is non-zero only if neutrino oscillation violates CP symmetry. This is expected, but not yet observed experimentally. If experiment shows this 3×3 matrix to be not unitary, a sterile neutrino
Sterile neutrino
Sterile neutrinosIn scientific literature, these particles are also variously referred to as right-handed neutrinos, inert neutrinos, heavy neutrinos, or neutral heavy leptons . are a hypothetical type of neutrino that do not interact via any of the fundamental interactions of the Standard Model...
or some other new physics is required.
Propagation and interference
Since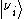 are mass eigenstates, their propagation can be described by plane wavePlane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
solutions of the form
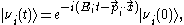
where
- quantities are expressed in natural unitsNatural unitsIn physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
-
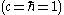
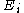is the energyEnergyIn physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of the mass-eigenstate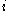
, -
is the time from the start of the propagation, -
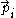is the three-dimensional momentumMomentumIn classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, -
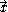is the current position of the particle relative to its starting position
In the ultrarelativistic limit
Ultrarelativistic limit
In physics, a particle is called ultrarelativistic when its speed is very close to the speed of light c.Max Planck showed that the relativistic expression for the energy of a particle whose rest mass is m and momentum is p is given by E^2 = m^2 c^4 + p^2 c^2...
,
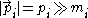, we can approximate the energy as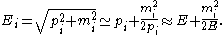This limit applies to all practical (currently observed) neutrinos, since their masses are less than 1 eV and their energies are at least 1 MeV, so the Lorentz factor
Lorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
γ is greater than 106 in all cases. Using also t ≈ L, where L is the distance traveled and also dropping the phase factors, the wavefunction becomes:
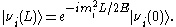
Eigenstates with different masses propagate at different speeds. The heavier ones lag behind while the lighter ones pull ahead. Since the mass eigenstates are combinations of flavor eigenstates, this difference in speed causes interference between the corresponding flavor components of each mass eigenstate. Constructive interference
Interference
In physics, interference is a phenomenon in which two waves superpose to form a resultant wave of greater or lower amplitude. Interference usually refers to the interaction of waves that are correlated or coherent with each other, either because they come from the same source or because they have...
causes it to be possible to observe a neutrino created with a given flavor to change its flavor during its propagation. The probability that a neutrino originally of flavor α will later be observed as having flavor β is
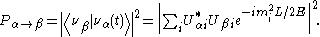
This is more conveniently written as
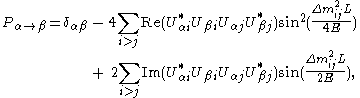
where
. The phase that is responsible for oscillation is often written as (with c and 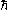restored)where 1.267 is unitless. In this form, it is convenient to plug in the oscillation parameters since:
- The mass differences, Δm2, are known to be on the order of
- Oscillation distances, L, in modern experiments are on the order of kilometers
- Neutrino energies, E, in modern experiments are typically on order of MeV or GeV.
If there is no CP-violation (δ is zero), then the second sum is zero.
Two neutrino case
The above formula is correct for any number of neutrino generations. Writing it explicitly in terms of mixing angles is extremely cumbersome if there are more than two neutrinos that participate in mixing. Fortunately, there are several cases in which only two neutrinos participate significantly. In this case, it is sufficient to consider the mixing matrix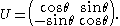Then the probability of a neutrino changing its flavor is
Or, using SI units and the convention introduced above
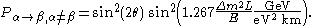
This formula is often appropriate for discussing the transition νμ ↔ ντ in atmospheric mixing, since the electron neutrino plays almost no role in this case. It is also appropriate for the solar case of νe ↔ νx, where νx is a superposition of νμ and ντ. These approximations are possible because the mixing angle θ13 is very small and because two of the mass states are very close in mass compared to the third.
Classical analogue of neutrino oscillation
The basic physics behind neutrino oscillation can be found in any system of coupled harmonic oscillatorHarmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
s. A simple example is a system of two pendulum
Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
s connected by a weak spring (a spring with a small spring constant). The first pendulum is set in motion by the experimenter while the second begins at rest. Over time, the second pendulum begins to swing under the influence of the spring, while the first pendulum's amplitude decreases as it loses energy to the second. Eventually all of the system's energy is transferred to the second pendulum and the first is at rest. The process then reverses. The energy oscillates between the two pendulums repeatedly until it is lost to friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
.
The behavior of this system can be understood by looking at its normal modes of oscillation. If the two pendulums are identical then one normal mode consists of both pendulums swinging in the same direction with a constant distance between them, while the other consists of the pendulums swinging in opposite (mirror image) directions. These normal modes have (slightly) different frequencies because the second involves the (weak) spring while the first does not. The initial state of the two-pendulum system is a combination of both normal modes. Over time, these normal modes drift out of phase, and this is seen as a transfer of motion from the first pendulum to the second.
When the pendulums are not identical the analysis is slightly more complicated. In the small-angle approximation, the potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
of a single pendulum system is
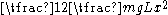, where g is the standard gravityStandard gravity
Standard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about...
, L is the length of the pendulum, m is the mass of the pendulum bob, and x is the horizontal displacement of the pendulum bob. As an isolated system the pendulum is a harmonic oscillator with a frequency of
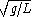. The potential energy of a spring is 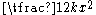where k is the spring constant and x is the displacement. With a mass attached it oscillates with a period of 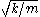. With two pendulums (labeled a and b) of equal mass but possibly unequal lengths and connected by a spring, the total potential energy isThis is a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
in xa and xb, which can also be written as a matrix product:
The 2×2 matrix is real symmetric and so (by the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
) it is "orthogonally
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
diagonalizable
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
". That is, there is an angle θ such that if we define
then
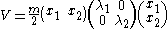
where λ1 and λ2 are the eigenvalues of the matrix. The variables x1 and x2 describe normal modes which oscillate with frequencies of
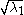and 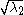. When the two pendulums are identical (La = Lb), θ is 45°.The description of the system in terms of the two pendulums (a and b) is analogous to the flavor basis of neutrinos. These are the parameters that are most easily produced and detected (in the case of neutrinos, by weak interactions involving the W boson). The description in terms of normal modes is analogous to the mass basis of neutrinos. These modes do not interact with each other when the system is free of outside influence. The angle θ is analogous to the Cabibbo angle (though that angle applies to quarks rather than neutrinos).
When the number of oscillators (particles) is increased to three, the orthogonal matrix can no longer be described by a single angle; instead, three are required (Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
). Furthermore, in the quantum case, the matrices may be complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. This requires the introduction of complex phases in addition to the rotation angles, which are associated with CP violation
CP violation
In particle physics, CP violation is a violation of the postulated CP-symmetry: the combination of C-symmetry and P-symmetry . CP-symmetry states that the laws of physics should be the same if a particle were interchanged with its antiparticle , and left and right were swapped...
but do not influence the observable effects of neutrino oscillation.
Two neutrino probabilities in vacuum
In the approximation where only two neutrinos participate in the oscillation, the probability of oscillation follows a simple pattern:The blue curve shows the probability of the original neutrino retaining its identity. The red curve shows the probability of conversion to the other neutrino. The maximum probability of conversion is equal to sin22θ. The frequency of the oscillation is controlled by Δm2.
Three neutrino probabilities
If three neutrinos are considered, the probability for each neutrino to appear is somewhat complex. Here are shown the probabilities for each initial flavor, with one plot showing a long range to display the slow "solar" oscillation and the other zoomed in to display the fast "atmospheric" oscillation. The oscillation parameters used here are consistent with current measurements, but since some parameters are still quite uncertain, these graphs are only qualitatively correct in some aspects. These values were used:- sin22θ13 = 0.10 (If it turns out to be much smaller or zero, the small wiggles shown here will be much smaller or non-existent, respectively.)
- sin22θ23 = 0.97 (It may turn out to be exactly one.)
- sin22θ12 = 0.861.
- δ = 0 (If it is actually large, these probabilities will be somewhat distorted and different for neutrinos and antineutrinos.)
- Δm = .
- Δm ≈ Δm = .
- Normal mass hierarchy.
Observed values of oscillation parameters
- sin2(θ13) < at 95% confidence level (θ13 < )
- tan2(θ12) = . This corresponds to θ12 ≡ θsol = ("sol" stands for solar)
- sin2(2θ23) = , corresponding to θ23 ≡ θatm = ("atm" stands for atmospheric)
- Δm ≡ Δm =
- |Δm| ≈ |Δm| ≡ Δm =
- δ, α1, α2, and the sign of Δm are currently unknown
Solar neutrino experiments combined with KamLAND
Kamioka Liquid Scintillator Antineutrino Detector
The Kamioka Liquid Scintillator Antineutrino Detector is an experiment at the Kamioka Observatory, an underground neutrino observatory near Toyama, Japan. It was built to detect electron antineutrinos. The experiment is situated in the old Kamiokande cavity in a horizontal mine drift in the...
have measured the so-called solar parameters Δm and sin2θsol. Atmospheric neutrino experiments such as Super-Kamiokande
Super-Kamiokande
Super-Kamiokande is a neutrino observatory which is under Mount Kamioka near the city of Hida, Gifu Prefecture, Japan...
together with the K2K and MINOS long baseline accelerator neutrino experiment have determined the so-called atmospheric parameters Δm and sin2θatm.
For atmospheric neutrinos (where the relevant difference of masses is about and the typical energies are ), oscillations become visible for neutrinos traveling several hundred km, which means neutrinos that reach the detector from below the horizon.
From atmospheric and solar neutrino
Solar neutrino
Electron neutrinos are produced in the Sun as a product of nuclear fusion. By far the largest fraction of neutrinos passing through the Earth are Solar neutrinos....
oscillation experiments, it is known that two mixing angles of the MNS matrix are large and the third is smaller. This is in sharp contrast to the CKM matrix in which all three angles are small and hierarchically decreasing. Nothing is known about the CP-violating phase of the MNS matrix.
If the neutrino mass proves to be of Majorana
Majorana fermion
In physics, a Majorana fermion is a fermion which is its own anti-particle. The term is used in opposition to Dirac fermion, which describes particles that differ from their antiparticles...
type (making the neutrino its own antiparticle), it is possible that the MNS matrix has more than one phase.
Since experiments observing neutrino oscillation measure the squared mass difference and not absolute mass, one can claim that the lightest neutrino mass is exactly zero, without contradicting observations. This is however regarded as unlikely by theorists.
Origins of neutrino mass
The question of how neutrino masses arise has not been answered conclusively. In the Standard Model of particle physics, fermionFermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s only have mass because of interactions with the Higgs field (see Higgs boson
Higgs boson
The Higgs boson is a hypothetical massive elementary particle that is predicted to exist by the Standard Model of particle physics. Its existence is postulated as a means of resolving inconsistencies in the Standard Model...
). These interactions involve both left- and right-handed versions of the fermion (see chirality
Chirality (physics)
A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
). However, only left-handed neutrinos have been observed so far.
Neutrinos may have another source of mass through the Majorana
Majorana fermion
In physics, a Majorana fermion is a fermion which is its own anti-particle. The term is used in opposition to Dirac fermion, which describes particles that differ from their antiparticles...
mass term. This type of mass applies for electrically-neutral particles since otherwise it would allow particles to turn into anti-particles, which would violate conservation of electric charge.
The smallest modification to the Standard Model, which only has left-handed neutrinos, is to allow these left-handed neutrinos to have Majorana masses. The problem with this is that the neutrino masses are implausibly smaller than the rest of the known particles (at least 500,000 times smaller than the mass of an electron), which, while it does not invalidate the theory, is not very satisfactory.
The next simplest addition would be to add right-handed neutrinos into the Standard Model, which interact with the left-handed neutrinos and the Higgs field in an analogous way to the rest of the fermions. These new neutrinos would interact with the other fermions solely in this way, so are not phenomenologically excluded. The problem of the disparity of the mass scales remains.
Seesaw mechanism
The most popular conjectured solution currently is the seesaw mechanism, where right-handed neutrinos with very large Majorana masses are added. If the right-handed neutrinos are very heavy, they induce a very small mass for the left-handed neutrinos, which is proportional to the inverse of the heavy mass.If it is assumed that the neutrinos interact with the Higgs field with approximately the same strengths as the charged fermions do, the heavy mass should be close to the GUT scale. Note that, in the Standard Model there is just one fundamental mass scale (which can be taken as the scale of breaking) and all masses (such as the electron or the mass of the Z boson) have to originate from this one.
There are other varieties of seesaw and currently it is not clear which, if any, nature has chosen.
The apparently innocent addition of right-handed neutrinos has the effect of adding new mass scales, completely unrelated to the mass scale of the Standard Model. Thus, heavy right-handed neutrinos look to be the first real glimpse of physics beyond the Standard Model. It is interesting to note that right-handed neutrinos can help to explain the origin of matter through a mechanism known as leptogenesis
Leptogenesis (physics)
In physical cosmology, leptogenesis is the generic term for hypothetical physical processes that produced an asymmetry between leptons and antileptons in the very early universe, resulting in the dominance of leptons over antileptons...
.
Other sources
There are alternative ways to modify the standard model that are similar to the addition of heavy right-handed neutrinos (e.g., the addition of new scalars or fermions in triplet states) and other modifications that are less similar (e.g., neutrino masses from loop effects and/or from suppressed couplings). One example of the last type of models is provided by certain versions supersymmetric extensions of the standard model of fundamental interactions, where R parity is not a symmetry. There, the exchange of supersymmetric particles such as squarks and sleptons can break the lepton number and lead to neutrino masses. These interactions are normally excluded from theories as they come from a class of interactions that lead to unacceptably rapid proton decayProton decay
In particle physics, proton decay is a hypothetical form of radioactive decay in which the proton decays into lighter subatomic particles, such as a neutral pion and a positron...
if they are all included. These models have little predictive power and are not able to provide a cold dark matter candidate but they are considered interesting since they would be compatible with new observable signals in particle colliders.
External links
- Maury Goodman, "The Neutrino Oscillation Industry" (2006). (Provides links to many other neutrino oscillation websites.)
- Review Articles on arxiv.org