Soliton (optics)
Encyclopedia
In optics
, the term soliton is used to refer to any optical field
that does not change during propagation because of a delicate balance between nonlinear
and linear effects in the medium. There are two main kinds of solitons:
. As shown in the picture on the right, an optical field approaches the lens and then it is focused. The effect of the lens is to introduce a non-uniform phase change that causes focusing. This phase change is a function of the space and can be represented with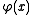
, whose shape is approximately represented in the picture.
The phase change can be expressed as the product of the phase constant and the width of the path the field has covered. We can write it as: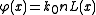
where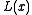
is the width of the lens, changing in each point with a shape that is the same of 
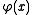because 
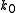and n are constants. In other words, in order to get a focusing effect we just have to introduce a phase change of such a shape, but we are not obliged to change the width. If we leave the width L fixed in each point, but we change the value of the refractive index
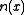we will get exactly the same effect, but with a completely different approach.
That's the way graded-index fiber
s work: the change in the refractive index introduces a focusing effect that can balance the natural diffraction of the field. If the two effects balance each other perfectly, then we have a confined field propagating within the fiber.
Spatial solitons are based on the same principle: the Kerr effect
introduces a Self-phase modulation
that changes the refractive index according to the intensity: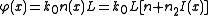
if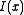
has a shape similar to the one shown in the figure, then we have created the phase behavior we wanted and the field will show a self-focusing effect. In other words, the field creates a fiber-like guiding structure while propagating. If the field creates a fiber and it is the mode of such a fiber at the same time, it means that the focusing nonlinear and diffractive linear effects are perfectly balanced and the field will propagate forever without changing its shape (as long as the medium does not change and if we can neglect losses, obviously). In order to have a self-focusing effect, we must have a positive 
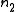, otherwise we will get the opposite effect and we will not notice any nonlinear behavior.
The optical waveguide the soliton creates while propagating is not only a mathematical model, but it actually exists and can be used to guide other waves at different frequencies. This way it is possible to let light interact with light at different frequencies (this is impossible in linear media)
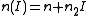
we remember that the relationship between intensity and electric field is (in the complex representation):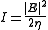
where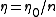
and 
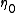is the impedance of free space, given by: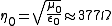
The field is propagating in the
direction with a phase constant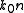 
. About now, we will ignore any dependence on the y axis, assuming that it is infinite in that direction. Then the field can be expressed as: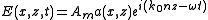
where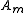
is the maximum amplitude of the field and 
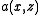is a dimensionless normalized function (so that its maximum value is 1) that represents the shape of the electric field among the x axis. In general it depends on z because fields change their shape while propagating.
Now we have to solve Helmholtz equation
:
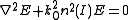
where it was pointed out clearly that the refractive index (thus the phase constant) depend on intensity. If we replace the expression of the electric field in the equation, assuming that the envelope
changes slowly while propagating, i.e.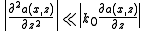
the equation becomes: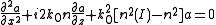
Let us introduce an approximation that is valid because the nonlinear effects are always much smaller than the linear ones: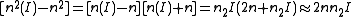
now we express the intensity in terms of the electric field: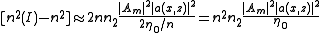
the equation becomes: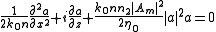
We will now assume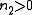
so that the nonlinear effect will cause self focusing. In order to make this evident, we will write in the equation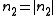 
Let us now define some parameters and replace them in the equation:
The equation becomes:
this is a common equation known as nonlinear Schrödinger equation
. From this form, we can understand the physical meaning of the parameter N:
For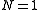
the solution of the equation is simple and it is the fundamental soliton: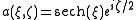
where sech is the hyperbolic secant
. It still depends on z, but only in phase, so the shape of the field will not change during propagation.
For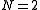
it is still possible to express the solution in a closed form, but it has a more complicated form: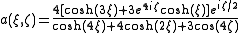
It does change its shape during propagation, but it is a periodic function of z with period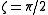
.
For soliton solutions, N must be an integer and it is said to be the order or the soliton. For higher values of N, there are no closed form expressions, but the solitons exist and they are all periodic with different periods. Their shape can easily be expressed only immediately after generation: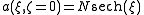
on the right there is the plot of the second order soliton: at the beginning it has a shape of a sech, then the maximum amplitude increases and then comes back to the sech shape. Since high intensity is necessary to generate solitons, if the field increases its intensity even further the medium could be damaged.
The condition to be solved if we want to generate a fundamental soliton is obtained expressing N in terms of all the known parameters and then putting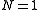
:
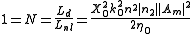
that, in terms of maximum intensity value becomes:
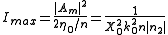
in most of the cases, the two variables that can be changed are the maximum intensity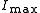
and the pulse width 
.
s, also referred to as nematicon
s.
in optical fibers is group velocity dispersion
. It is because generated impulses have a non-zero bandwidth and the medium they are propagating through has a refractive index that depends on frequency
(or wavelength
). This effect is represented by the group delay dispersion parameter D; using it, it is possible to calculate exactly how much the pulse will widen:
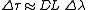
where L is the length of the fiber and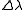
is the bandwidth in terms of wavelength. The approach in modern communication systems is to balance such a dispersion with other fibers having D with different signs in different parts of the fiber: this way the pulses keep on broadening and shrinking while propagating. With temporal solitons it is possible to remove such a problem completely.
Consider the picture on the right. On the left there is a standard Gaussian pulse, that's the envelope of the field oscillating at a defined frequency. We assume that the frequency remains perfectly constant during the pulse.
Now we let this pulse propagate through a fiber with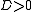
, it will be affected by group velocity dispersion. For this sign of D, the dispersion is anomalous, so that the higher frequency components will propagate a little bit faster than the lower frequencies, thus arriving before at the end of the fiber. The overall signal we get is a wider chirped pulse, shown in the upper right of the picture.
Now let us assume we have a medium that shows only nonlinear Kerr effect but its refractive index does not depend on frequency: such a medium does not exist, but it's worth considering it to understand the different effects.
The phase of the field is given by: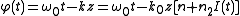
the frequency (according to its definition) is given by:
this situation is represented in the picture on the left. At the beginning of the pulse the frequency is lower, at the end it's higher. After the propagation through our ideal medium, we will get a chirped pulse with no broadening because we have neglected dispersion.
Coming back to the first picture, we see that the two effects introduce a change in frequency in two different opposite directions. It is possible to make a pulse so that the two effects will balance each other. Considering higher frequencies, linear dispersion will tend to let them propagate faster, while nonlinear Kerr effect will slow them down. The overall effect will be that the pulse does not change while propagating: such pulses are called temporal solitons.
of AT&T
Bell Labs
were the first to suggest that solitons could exist in optical fiber
s, due to a balance between self-phase modulation
and anomalous dispersion
.
Also in 1973 Robin Bullough
made the first mathematical report of the existence of optical solitons. He also proposed the idea of a soliton-based transmission system to increase performance of optical telecommunication
s.
Solitons in a fiber optic system are described by the Manakov equations.
In 1987, P. Emplit, J.P. Hamaide, F. Reynaud, C. Froehly and A. Barthelemy, from the Universities of Brussels and Limoges, made the first experimental observation of the propagation of a dark soliton, in an optical fiber.
In 1988, Linn Mollenauer and his team transmitted soliton pulses over 4,000 kilometers using a phenomenon called the Raman effect, named for the Indian scientist Sir C. V. Raman
who first described it in the 1920s, to provide optical gain in the fiber.
In 1991, a Bell Labs research team transmitted solitons error-free at 2.5 gigabits over more than 14,000 kilometers, using erbium
optical fiber amplifiers (spliced-in segments of optical fiber containing the rare earth element erbium). Pump lasers, coupled to the optical amplifiers, activate the erbium, which energizes the light pulses.
In 1998, Thierry Georges and his team at France Télécom
R&D Center, combining optical solitons of different wavelengths (wavelength division multiplexing), demonstrated a data transmission of 1 terabit
per second (1,000,000,000,000 units of information per second).
In 2001, the practical use of solitons became a reality when Algety Telecom deployed submarine telecommunications equipment in Europe carrying real traffic using John Scott Russell
's solitary wave.
) that limits the power on the xy plane. If the field is propagating towards z with a phase constant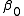
, then it can be expressed in the following form: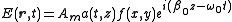
where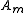
is the maximum amplitude of the field, 
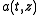is the envelope that shapes the impulse in the time domain; in general it depends on z because the impulse can change its shape while propagating; 
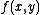represents the shape of the field on the xy plane, and it does not change during propagation because we have assumed the field is guided. Both a and f are normalized dimensionless functions whose maximum value is 1, so that 
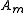really represents the field amplitude.
Since in the medium there is a dispersion we can not neglect, the relationship between the electric field and its polarization is given by a convolution
integral. Anyway, using a representation in the Fourier domain
, we can replace the convolution with a simple product, thus using standard relationships that are valid in simpler media. We Fourier-transform the electric field using the following definition:
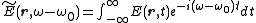
using this definition, a derivative in the time domain corresponds to a product in the Fourier domain:
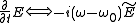
the complete expression of the field in the frequency domain is:
Now we can solve Helmholtz equation
in the frequency domain:
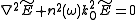
we decide to express the phase constant with the following notation: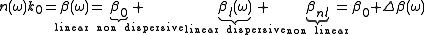
where we assume that
(the sum of the linear dispersive component and the non linear part) is a small perturbation, i.e.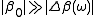 
. The phase constant can have any complicated behavior, but we can represent it with a Taylor series
centered on
:
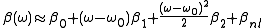
where, as known: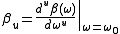
we put the expression of the electric field in the equation and make some calculations. If we assume the slowly varying envelope approximation
:
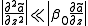
we get:
we are ignoring the behavior in the xy plane, because it is already known and given by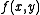
.
We make a small approximation, as we did for the spatial soliton:
replacing this in the equation we get simply: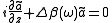
now we want to come back in the time domain. Expressing the products by derivatives we get the duality: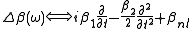
we can write the non linear component in terms of the amplitude of the field: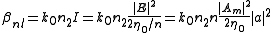
for duality with the spatial soliton, we define: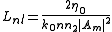
and this symbol has the same meaning of the previous case, even if the context is different. The equation becomes: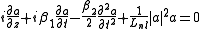
We know that the impulse is propagating among the z axis with a group velocity
given by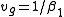
, so we are not interested in it because we just want to know how the pulse changes its shape while propagating. We decide to study the impulse shape, i.e. the envelope function a(.) using a reference that is moving with the field at the same velocity. Thus we make the substitution
and the equation becomes: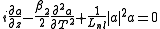
we assume the medium where the field is propagating to show anomalous dispersion, i.e.
or in term of the group delay dispersion parameter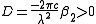 
. We make this more evident replacing in the equation 
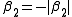. Let us define now the following parameters (the duality with the previous case is evident):
replacing those in the equation we get: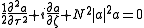
that is exactly the same equation we have obtained in the previous case. The first order soliton is given by: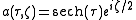
the same considerations we have made are valid in this case. The condition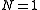
becomes a condition on the amplitude of the electric field: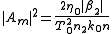
or, in terms of intensity: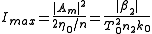
or we can express it in terms of power if we introduce an effective area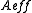
defined so that 
:
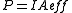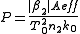
If we create such a soliton using slightly wrong power or shape, then it will adjust itself until it reaches the standard sech shape with the right power. Unfortunately this is achieved at the expense of some power loss, that can cause problems because it can generate another non-soliton field propagating together with the field we want. Mono-dimensional solitons are very stable: for example, if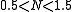
we will generate a first order soliton anyway; if N is greater we'll generate a higher order soliton, but the focusing it does while propagating may cause high power peaks damaging the media.
The only way to create a (1 + 1) D spatial soliton is to limit the field on the y axis using a dielectric slab
, then limiting the field on x using the soliton.
On the other hand, (2 + 1) D spatial solitons are unstable, so any small perturbation (due to noise, for example) can cause the soliton to diffract as a field in a linear medium or to collapse, thus damaging the material. It is possible to create stable (2 + 1) D spatial solitons using saturating nonlinear media, where the Kerr relationship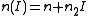
is valid until it reaches a maximum value. Working close to this saturation level makes it possible to create a stable soliton in a three dimensional space.
If we consider the propagation of shorter (temporal) light pulses or over a longer distance, we need to consider higher-order corrections and
therefore the pulse carrier envelope is governed by the higher-order nonlinear Schrödinger equation (HONSE) for which there are some specialized (analytical) soliton solutions.
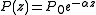
this is a serious problem for temporal solitons propagating in fibers for several kilometers. Let us consider what happens for the temporal soliton, generalization to the spatial ones is immediate. We have proved that the relationship between power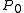
and impulse length 
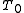is: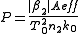
if the power changes, the only thing that can change in the second part of the relationship is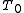
. if we add losses to the power and solve the relationship in terms of 
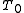we get:
the width of the impulse grows exponentially to balance the losses! this relationship is true as long as the soliton exists, i.e. until this perturbation is small, so it must be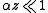
otherwise we can not use the equations for solitons and we have to study standard linear dispersion. If we want to create a transmission system using optical fibers and solitons, we have to add optical amplifier
s in order to limit the loss of power.
on Single mode optical fiber of considerable length (50-100m) to compensate group velocity dispersion (GVD) and subsequent evolution of soliton pulse ( peak energy, narrow, secant hyperbolic pulse). Generation of soliton pulse in fiber is an obvious conclusion as self phase modulation due to high energy of pulse offset GVD, whereas the evolution length is 2000 km. (the laser wavelength chosen greater than 1.3 micrometers). Moreover peak soliton pulse is of period 1-3ps so that it is safely accommodated in the optical bandwidth. Once soliton pulse is generated it is least dispersed over thousands of kilometers length of fiber limiting the number of repeater station.
Is it possible to obtain solitons if those conditions are not verified? if we assume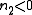
or 
, we get the following differential equation (it has the same form in both cases, we will use only the notation of the temporal soliton):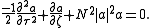
This equation has soliton-like solutions. For the first order (N=1):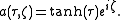
The plot of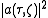
is shown in the picture on the right. For higher order solitons (
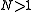) we can use the following closed form expression:
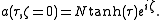
It is a soliton, in the sense that it propagates without changing its shape, but it is not made by a normal pulse; rather, it is a lack of energy in a continuous time beam. The intensity is constant, but for a short time during which it jumps to zero and back again, thus generating a "dark pulse"'. Those solitons can actually be generated introducing short dark pulses in much longer standard pulses. Dark solitons are more difficult to handle than standard solitons, but they have shown to be more stable and robust to losses.
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, the term soliton is used to refer to any optical field
Optical field
The optical field is a term used in physics and vector calculus to designate the electric field shown as E in the electromagnetic wave equation which can be derived from Maxwell's Equations...
that does not change during propagation because of a delicate balance between nonlinear
Nonlinearity
In mathematics, a nonlinear system is one that does not satisfy the superposition principle, or one whose output is not directly proportional to its input; a linear system fulfills these conditions. In other words, a nonlinear system is any problem where the variable to be solved for cannot be...
and linear effects in the medium. There are two main kinds of solitons:
- spatial solitons: the nonlinear effect can balance the diffractionDiffractionDiffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
. The electromagnetic field can change the refractive indexRefractive indexIn optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
of the medium while propagating, thus creating a structure similar to a graded-index fiberGraded-index fiberIn fiber optics, a graded-index or gradient-index fiber is an optical fiber whose core has a refractive index that decreases with increasing radial distance from the fiber axis ....
. If the field is also a propagating mode of the guide it has created, then it will remain confined and it will propagate without changing its shape - temporal solitons: if the electromagnetic field is already spatially confined, it is possible to send pulses that will not change their shape because the nonlinear effects will balance the dispersionDispersionDispersion may refer to:In physics:*The dependence of wave velocity on frequency or wavelength:**Dispersion , for light waves**Dispersion **Acoustic dispersion, for sound waves...
. Those solitons were discovered first and they are often simply referred as "solitons" in optics.
Spatial solitons
In order to understand how a spatial soliton can exist, we have to make some considerations about a simple convex lensLens (optics)
A lens is an optical device with perfect or approximate axial symmetry which transmits and refracts light, converging or diverging the beam. A simple lens consists of a single optical element...
. As shown in the picture on the right, an optical field approaches the lens and then it is focused. The effect of the lens is to introduce a non-uniform phase change that causes focusing. This phase change is a function of the space and can be represented with
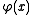, whose shape is approximately represented in the picture.The phase change can be expressed as the product of the phase constant and the width of the path the field has covered. We can write it as:
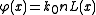
where
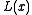is the width of the lens, changing in each point with a shape that is the same of 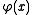because 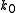and n are constants. In other words, in order to get a focusing effect we just have to introduce a phase change of such a shape, but we are not obliged to change the width. If we leave the width L fixed in each point, but we change the value of the refractive indexRefractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
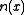we will get exactly the same effect, but with a completely different approach.That's the way graded-index fiber
Graded-index fiber
In fiber optics, a graded-index or gradient-index fiber is an optical fiber whose core has a refractive index that decreases with increasing radial distance from the fiber axis ....
s work: the change in the refractive index introduces a focusing effect that can balance the natural diffraction of the field. If the two effects balance each other perfectly, then we have a confined field propagating within the fiber.
Spatial solitons are based on the same principle: the Kerr effect
Kerr effect
The Kerr effect, also called the quadratic electro-optic effect , is a change in the refractive index of a material in response to an applied electric field. The Kerr effect is distinct from the Pockels effect in that the induced index change is directly proportional to the square of the electric...
introduces a Self-phase modulation
Self-phase modulation
Self-phase modulation is a nonlinear optical effect of light-matter interaction.An ultrashort pulse of light, when travelling in a medium, will induce a varying refractive index of the medium due to the optical Kerr effect...
that changes the refractive index according to the intensity:
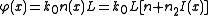
if
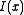has a shape similar to the one shown in the figure, then we have created the phase behavior we wanted and the field will show a self-focusing effect. In other words, the field creates a fiber-like guiding structure while propagating. If the field creates a fiber and it is the mode of such a fiber at the same time, it means that the focusing nonlinear and diffractive linear effects are perfectly balanced and the field will propagate forever without changing its shape (as long as the medium does not change and if we can neglect losses, obviously). In order to have a self-focusing effect, we must have a positive 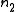, otherwise we will get the opposite effect and we will not notice any nonlinear behavior.The optical waveguide the soliton creates while propagating is not only a mathematical model, but it actually exists and can be used to guide other waves at different frequencies. This way it is possible to let light interact with light at different frequencies (this is impossible in linear media)
Proof
An electric field is propagating in a medium showing optical Kerr effect, so the refractive index is given by: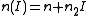we remember that the relationship between intensity and electric field is (in the complex representation):
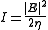
where
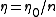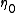and is the impedance of free space, given by: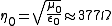The field is propagating in the
direction with a phase constant 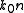. About now, we will ignore any dependence on the y axis, assuming that it is infinite in that direction. Then the field can be expressed as: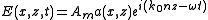where
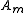is the maximum amplitude of the field and 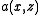is a dimensionless normalized function (so that its maximum value is 1) that represents the shape of the electric field among the x axis. In general it depends on z because fields change their shape while propagating.Now we have to solve Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
:
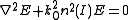
where it was pointed out clearly that the refractive index (thus the phase constant) depend on intensity. If we replace the expression of the electric field in the equation, assuming that the envelope
changes slowly while propagating, i.e.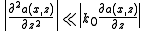the equation becomes:
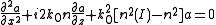
Let us introduce an approximation that is valid because the nonlinear effects are always much smaller than the linear ones:
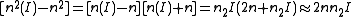
now we express the intensity in terms of the electric field:
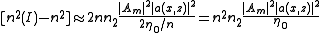
the equation becomes:
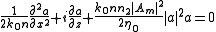
We will now assume
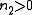so that the nonlinear effect will cause self focusing. In order to make this evident, we will write in the equation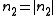 Let us now define some parameters and replace them in the equation:
-
, so we can express the dependence on the x axis with a dimensionless parameter;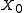 
is a length, whose physical meaning will be clearer later. -
, after the electric field has propagated across z for this length, the linear effects of diffraction can not be neglected anymore. -
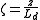, for studying the z-dependence with a dimensionless variable. -
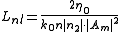, after the electric field has propagated across z for this length, the nonlinear effects can not be neglected anymore. This parameter depends upon the intensity of the electric field, that's typical for nonlinear parameters. -
The equation becomes:
this is a common equation known as nonlinear Schrödinger equation
Nonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
. From this form, we can understand the physical meaning of the parameter N:
- if
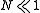, then we can neglect the nonlinear part of the equation. It means 
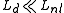, then the field will be affected by the linear effect (diffraction) much earlier than the nonlinear effect, it will just diffract without any nonlinear behavior. - if
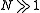, then the nonlinear effect will be more evident than diffraction and, because of self phase modulation, the field will tend to focus. - if
, then the two effects balance each other and we have to solve the equation.
For
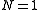the solution of the equation is simple and it is the fundamental soliton: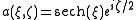where sech is the hyperbolic secant
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
. It still depends on z, but only in phase, so the shape of the field will not change during propagation.
For
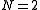it is still possible to express the solution in a closed form, but it has a more complicated form: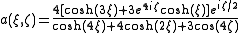It does change its shape during propagation, but it is a periodic function of z with period
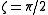.For soliton solutions, N must be an integer and it is said to be the order or the soliton. For higher values of N, there are no closed form expressions, but the solitons exist and they are all periodic with different periods. Their shape can easily be expressed only immediately after generation:
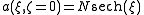
on the right there is the plot of the second order soliton: at the beginning it has a shape of a sech, then the maximum amplitude increases and then comes back to the sech shape. Since high intensity is necessary to generate solitons, if the field increases its intensity even further the medium could be damaged.
The condition to be solved if we want to generate a fundamental soliton is obtained expressing N in terms of all the known parameters and then putting
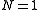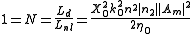
:that, in terms of maximum intensity value becomes:
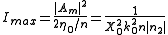
in most of the cases, the two variables that can be changed are the maximum intensity
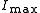and the pulse width .Generation of Spatial Solitons
The first experiment on spatial optical solitons was reported in 1974 by Ashkin and Bjorkholm in a cell filled with sodium vapor. It was more than another ten years before this field was revisited in experiments at Limoge University in liquid carbon disulphide. After these experiments spatial solitons have been demonstrated in glass, semiconductors and polymers. During the last decade several experiments have been reported on solitons in nematic liquid crystalLiquid crystal
Liquid crystals are a state of matter that have properties between those of a conventional liquid and those of a solid crystal. For instance, an LC may flow like a liquid, but its molecules may be oriented in a crystal-like way. There are many different types of LC phases, which can be...
s, also referred to as nematicon
Nematicon
In optics, a nematicon is a spatial optical soliton in a nematic liquid crystal. The name was invented in 2003 by G. Assanto . Nematicons are generated by the special type of optical nonlinearity that is present in nematic LCs: the optical field induced director reorientation...
s.
Temporal solitons
The main problem that limits transmission bit rateBit rate
In telecommunications and computing, bit rate is the number of bits that are conveyed or processed per unit of time....
in optical fibers is group velocity dispersion
Dispersion (optics)
In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media...
. It is because generated impulses have a non-zero bandwidth and the medium they are propagating through has a refractive index that depends on frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
(or wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
). This effect is represented by the group delay dispersion parameter D; using it, it is possible to calculate exactly how much the pulse will widen:
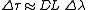
where L is the length of the fiber and
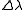is the bandwidth in terms of wavelength. The approach in modern communication systems is to balance such a dispersion with other fibers having D with different signs in different parts of the fiber: this way the pulses keep on broadening and shrinking while propagating. With temporal solitons it is possible to remove such a problem completely.Consider the picture on the right. On the left there is a standard Gaussian pulse, that's the envelope of the field oscillating at a defined frequency. We assume that the frequency remains perfectly constant during the pulse.
Now we let this pulse propagate through a fiber with
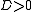, it will be affected by group velocity dispersion. For this sign of D, the dispersion is anomalous, so that the higher frequency components will propagate a little bit faster than the lower frequencies, thus arriving before at the end of the fiber. The overall signal we get is a wider chirped pulse, shown in the upper right of the picture.The phase of the field is given by:
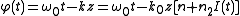
the frequency (according to its definition) is given by:
this situation is represented in the picture on the left. At the beginning of the pulse the frequency is lower, at the end it's higher. After the propagation through our ideal medium, we will get a chirped pulse with no broadening because we have neglected dispersion.
Coming back to the first picture, we see that the two effects introduce a change in frequency in two different opposite directions. It is possible to make a pulse so that the two effects will balance each other. Considering higher frequencies, linear dispersion will tend to let them propagate faster, while nonlinear Kerr effect will slow them down. The overall effect will be that the pulse does not change while propagating: such pulses are called temporal solitons.
History of temporal solitons
In 1973, Akira Hasegawa and Fred TappertFred Tappert
Frederick Drach Tappert was an American physicist whose primary contributions were in underwater acoustics. He is noted for the development of the parabolic equation model and split-step Fourier algorithm for electromagnetic and ocean acoustic propagation.He began his scientific career in the...
of AT&T
AT&T
AT&T Inc. is an American multinational telecommunications corporation headquartered in Whitacre Tower, Dallas, Texas, United States. It is the largest provider of mobile telephony and fixed telephony in the United States, and is also a provider of broadband and subscription television services...
Bell Labs
Bell Labs
Bell Laboratories is the research and development subsidiary of the French-owned Alcatel-Lucent and previously of the American Telephone & Telegraph Company , half-owned through its Western Electric manufacturing subsidiary.Bell Laboratories operates its...
were the first to suggest that solitons could exist in optical fiber
Optical fiber
An optical fiber is a flexible, transparent fiber made of a pure glass not much wider than a human hair. It functions as a waveguide, or "light pipe", to transmit light between the two ends of the fiber. The field of applied science and engineering concerned with the design and application of...
s, due to a balance between self-phase modulation
Self-phase modulation
Self-phase modulation is a nonlinear optical effect of light-matter interaction.An ultrashort pulse of light, when travelling in a medium, will induce a varying refractive index of the medium due to the optical Kerr effect...
and anomalous dispersion
Dispersion (optics)
In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media...
.
Also in 1973 Robin Bullough
Robin Bullough
Robin K. Bullough was a British Mathematical Physicist famous for his contributions to the theory of solitons, in particular for his role in the development of the theory of the optical soliton, now commonly used, for example, in the theory of trans-oceanic optical fibre communication theory, but...
made the first mathematical report of the existence of optical solitons. He also proposed the idea of a soliton-based transmission system to increase performance of optical telecommunication
Telecommunication
Telecommunication is the transmission of information over significant distances to communicate. In earlier times, telecommunications involved the use of visual signals, such as beacons, smoke signals, semaphore telegraphs, signal flags, and optical heliographs, or audio messages via coded...
s.
Solitons in a fiber optic system are described by the Manakov equations.
In 1987, P. Emplit, J.P. Hamaide, F. Reynaud, C. Froehly and A. Barthelemy, from the Universities of Brussels and Limoges, made the first experimental observation of the propagation of a dark soliton, in an optical fiber.
In 1988, Linn Mollenauer and his team transmitted soliton pulses over 4,000 kilometers using a phenomenon called the Raman effect, named for the Indian scientist Sir C. V. Raman
Chandrasekhara Venkata Raman
Sir Chandrasekhara Venkata Raman, FRS was an Indian physicist whose work was influential in the growth of science in the world. He was the recipient of the Nobel Prize for Physics in 1930 for the discovery that when light traverses a transparent material, some of the light that is deflected...
who first described it in the 1920s, to provide optical gain in the fiber.
In 1991, a Bell Labs research team transmitted solitons error-free at 2.5 gigabits over more than 14,000 kilometers, using erbium
Erbium
Erbium is a chemical element in the lanthanide series, with the symbol Er and atomic number 68. A silvery-white solid metal when artificially isolated, natural erbium is always found in chemical combination with other elements on Earth...
optical fiber amplifiers (spliced-in segments of optical fiber containing the rare earth element erbium). Pump lasers, coupled to the optical amplifiers, activate the erbium, which energizes the light pulses.
In 1998, Thierry Georges and his team at France Télécom
France Télécom
France Telecom S.A. is the main telecommunications company in France, the third-largest in Europe and one of the largest in the world. It currently employs about 180,000 people and has 192.7 million customers worldwide . In 2010 the group had revenue of €45.5 billion...
R&D Center, combining optical solitons of different wavelengths (wavelength division multiplexing), demonstrated a data transmission of 1 terabit
Binary prefix
In computing, a binary prefix is a specifier or mnemonic that is prepended to the units of digital information, the bit and the byte, to indicate multiplication by a power of 2...
per second (1,000,000,000,000 units of information per second).
In 2001, the practical use of solitons became a reality when Algety Telecom deployed submarine telecommunications equipment in Europe carrying real traffic using John Scott Russell
John Scott Russell
John Scott Russell was a Scottish naval engineer who built the Great Eastern in collaboration with Isambard Kingdom Brunel, and made the discovery that gave birth to the modern study of solitons.-Personal life:John Scott Russell was born John Russell on 9 May 1808 in Parkhead, Glasgow, the son of...
's solitary wave.
Proof
An electric field is propagating in a medium showing optical Kerr effect through a guiding structure (such as an optical fiberOptical fiber
An optical fiber is a flexible, transparent fiber made of a pure glass not much wider than a human hair. It functions as a waveguide, or "light pipe", to transmit light between the two ends of the fiber. The field of applied science and engineering concerned with the design and application of...
) that limits the power on the xy plane. If the field is propagating towards z with a phase constant
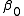, then it can be expressed in the following form: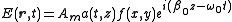where
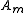is the maximum amplitude of the field, 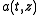is the envelope that shapes the impulse in the time domain; in general it depends on z because the impulse can change its shape while propagating; 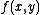represents the shape of the field on the xy plane, and it does not change during propagation because we have assumed the field is guided. Both a and f are normalized dimensionless functions whose maximum value is 1, so that 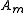really represents the field amplitude.Since in the medium there is a dispersion we can not neglect, the relationship between the electric field and its polarization is given by a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
integral. Anyway, using a representation in the Fourier domain
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, we can replace the convolution with a simple product, thus using standard relationships that are valid in simpler media. We Fourier-transform the electric field using the following definition:
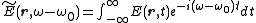
using this definition, a derivative in the time domain corresponds to a product in the Fourier domain:
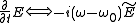
the complete expression of the field in the frequency domain is:
Now we can solve Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
in the frequency domain:
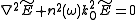
we decide to express the phase constant with the following notation:
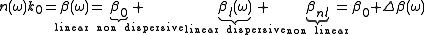
where we assume that
(the sum of the linear dispersive component and the non linear part) is a small perturbation, i.e. 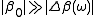. The phase constant can have any complicated behavior, but we can represent it with a Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
centered on
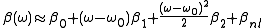
:where, as known:
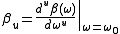
we put the expression of the electric field in the equation and make some calculations. If we assume the slowly varying envelope approximation
Slowly varying envelope approximation
In physics, the slowly varying envelope approximation is the assumption that the envelope of a forward-travelling wave pulse varies slowly in time and space compared to a period or wavelength...
:
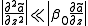
we get:
we are ignoring the behavior in the xy plane, because it is already known and given by
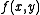.We make a small approximation, as we did for the spatial soliton:
replacing this in the equation we get simply:
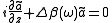
now we want to come back in the time domain. Expressing the products by derivatives we get the duality:
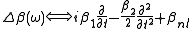
we can write the non linear component in terms of the amplitude of the field:
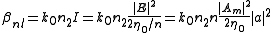
for duality with the spatial soliton, we define:
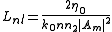
and this symbol has the same meaning of the previous case, even if the context is different. The equation becomes:
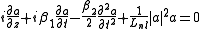
We know that the impulse is propagating among the z axis with a group velocity
Group velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
given by
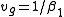, so we are not interested in it because we just want to know how the pulse changes its shape while propagating. We decide to study the impulse shape, i.e. the envelope function a(.) using a reference that is moving with the field at the same velocity. Thus we make the substitutionand the equation becomes:
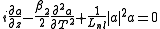
we assume the medium where the field is propagating to show anomalous dispersion, i.e.
or in term of the group delay dispersion parameter 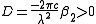. We make this more evident replacing in the equation 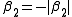. Let us define now the following parameters (the duality with the previous case is evident):replacing those in the equation we get:
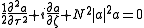
that is exactly the same equation we have obtained in the previous case. The first order soliton is given by:
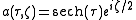
the same considerations we have made are valid in this case. The condition
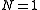becomes a condition on the amplitude of the electric field: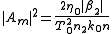or, in terms of intensity:
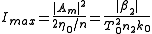
or we can express it in terms of power if we introduce an effective area
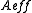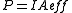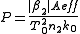
defined so that :Stability of solitons
We have described what optical solitons are and, using mathematics, we have seen that, if we want to create them, we have to create a field with a particular shape (just sech for the first order) with a particular power related to the duration of the impulse. But what if we are a bit wrong in creating such impulses? Adding small perturbations to the equations and solving them numerically, it is possible to show that mono-dimensional solitons are stable. They are often referred as (1 + 1) D solitons, meaning that they are limited in one dimension (x or t, as we have seen) and propagate in another one (z).If we create such a soliton using slightly wrong power or shape, then it will adjust itself until it reaches the standard sech shape with the right power. Unfortunately this is achieved at the expense of some power loss, that can cause problems because it can generate another non-soliton field propagating together with the field we want. Mono-dimensional solitons are very stable: for example, if
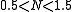we will generate a first order soliton anyway; if N is greater we'll generate a higher order soliton, but the focusing it does while propagating may cause high power peaks damaging the media.The only way to create a (1 + 1) D spatial soliton is to limit the field on the y axis using a dielectric slab
Waveguide (optics)
An optical waveguide is a physical structure that guides electromagnetic waves in the optical spectrum. Common types of optical waveguides include optical fiber and rectangular waveguides....
, then limiting the field on x using the soliton.
On the other hand, (2 + 1) D spatial solitons are unstable, so any small perturbation (due to noise, for example) can cause the soliton to diffract as a field in a linear medium or to collapse, thus damaging the material. It is possible to create stable (2 + 1) D spatial solitons using saturating nonlinear media, where the Kerr relationship
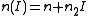is valid until it reaches a maximum value. Working close to this saturation level makes it possible to create a stable soliton in a three dimensional space.If we consider the propagation of shorter (temporal) light pulses or over a longer distance, we need to consider higher-order corrections and
therefore the pulse carrier envelope is governed by the higher-order nonlinear Schrödinger equation (HONSE) for which there are some specialized (analytical) soliton solutions.
Effect of power losses
As we have seen, in order to create a soliton it is necessary to have the right power when it is generated. If there are no losses in the medium, then we know that the soliton will keep on propagating forever without changing shape (1st order) or changing its shape periodically (higher orders). Unfortunately any medium introduces losses, so the actual behavior of power will be in the form: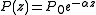this is a serious problem for temporal solitons propagating in fibers for several kilometers. Let us consider what happens for the temporal soliton, generalization to the spatial ones is immediate. We have proved that the relationship between power
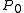and impulse length 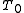is: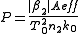if the power changes, the only thing that can change in the second part of the relationship is
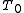. if we add losses to the power and solve the relationship in terms of 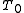we get:the width of the impulse grows exponentially to balance the losses! this relationship is true as long as the soliton exists, i.e. until this perturbation is small, so it must be
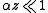otherwise we can not use the equations for solitons and we have to study standard linear dispersion. If we want to create a transmission system using optical fibers and solitons, we have to add optical amplifierOptical amplifier
An optical amplifier is a device that amplifies an optical signal directly, without the need to first convert it to an electrical signal. An optical amplifier may be thought of as a laser without an optical cavity, or one in which feedback from the cavity is suppressed...
s in order to limit the loss of power.
Generation of soliton pulse
Experiments has been carried out to analyze the effect of high frequency (20 MHz-1 GHz) external magnetic field induced nonlinear Kerr effectKerr effect
The Kerr effect, also called the quadratic electro-optic effect , is a change in the refractive index of a material in response to an applied electric field. The Kerr effect is distinct from the Pockels effect in that the induced index change is directly proportional to the square of the electric...
on Single mode optical fiber of considerable length (50-100m) to compensate group velocity dispersion (GVD) and subsequent evolution of soliton pulse ( peak energy, narrow, secant hyperbolic pulse). Generation of soliton pulse in fiber is an obvious conclusion as self phase modulation due to high energy of pulse offset GVD, whereas the evolution length is 2000 km. (the laser wavelength chosen greater than 1.3 micrometers). Moreover peak soliton pulse is of period 1-3ps so that it is safely accommodated in the optical bandwidth. Once soliton pulse is generated it is least dispersed over thousands of kilometers length of fiber limiting the number of repeater station.
Dark solitons
In the analysis of both types of solitons we have assumed particular conditions about the medium:- in spatial solitons,
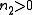, that means the self-phase modulation causes self-focusing - in temporal solitons,
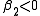or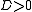 
, anomalous dispersion
Is it possible to obtain solitons if those conditions are not verified? if we assume
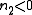or , we get the following differential equation (it has the same form in both cases, we will use only the notation of the temporal soliton):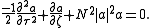This equation has soliton-like solutions. For the first order (N=1):
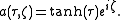
The plot of
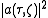is shown in the picture on the right. For higher order solitons (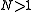) we can use the following closed form expression: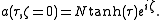It is a soliton, in the sense that it propagates without changing its shape, but it is not made by a normal pulse; rather, it is a lack of energy in a continuous time beam. The intensity is constant, but for a short time during which it jumps to zero and back again, thus generating a "dark pulse"'. Those solitons can actually be generated introducing short dark pulses in much longer standard pulses. Dark solitons are more difficult to handle than standard solitons, but they have shown to be more stable and robust to losses.
See also
- SolitonSolitonIn mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
- Self-phase modulationSelf-phase modulationSelf-phase modulation is a nonlinear optical effect of light-matter interaction.An ultrashort pulse of light, when travelling in a medium, will induce a varying refractive index of the medium due to the optical Kerr effect...
- Optical Kerr effect
- vector solitonVector solitonIn physical optics or wave optics, a vector soliton is a solitary wave with multiple components coupled together that maintains its shape during propagation. Ordinary solitons maintain their shape but have effectively only one polarization component, while vector solitons have two distinct...
- nematiconNematiconIn optics, a nematicon is a spatial optical soliton in a nematic liquid crystal. The name was invented in 2003 by G. Assanto . Nematicons are generated by the special type of optical nonlinearity that is present in nematic LCs: the optical field induced director reorientation...
- Ultrashort pulseUltrashort pulseIn optics, an ultrashort pulse of light is an electromagnetic pulse whose time duration is of the order of a femtosecond . Such pulses have a broadband optical spectrum, and can be created by mode-locked oscillators...