Slowly varying envelope approximation
Encyclopedia
In physics
, the slowly varying envelope approximation (SVEA) is the assumption that the envelope
of a forward-travelling wave
pulse varies slowly in time and space compared to a period or wavelength
. This requires the spectrum
of the signal to be narrow-banded—hence it also referred to as the narrow-band approximation.
The slowly varying envelope approximation is often used because the resulting equations are in many cases easier to solve than the original equations, reducing the order of—all or some of—the highest-order partial derivative
s. But the validity of the assumptions which are made need to be justified.
:
If k0 and ω0 are the wave number and angular frequency
of the (characteristic) carrier wave
for the signal E(r,t), the following representation is useful:
where
denotes the real part of the quantity between brackets.
In the slowly varying envelope approximation (SVEA) it is assumed that the complex-valued
amplitude
E0(r, t) only varies slowly with r and t. This inherently implies that E0(r, t) represents waves propagating forward, predominantly in the k0 direction. As a result of the slow variation of E0(r, t), when taking derivatives, the highest-order derivatives may be neglected:
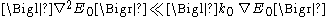and 
with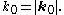 
It is convenient to choose k0 and ω0 such that they satisfy the dispersion relation
:
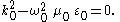
This gives the following approximation to the wave equation, as a result of the slowly varying envelope approximation:
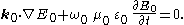
Which is a hyperbolic partial differential equation
, like the original wave equation, but now of first-order instead of second-order. And valid for coherent forward-propagating waves in directions near the k0-direction.
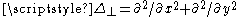is the Laplace operator
in the x–y plane, the result is:
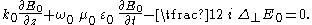
Which is a parabolic partial differential equation
. This equation has enhanced validity as compared to the full SVEA: it can represents waves propagating in directions significantly different from the z-direction.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the slowly varying envelope approximation (SVEA) is the assumption that the envelope
Envelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
of a forward-travelling wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
pulse varies slowly in time and space compared to a period or wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
. This requires the spectrum
Spectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
of the signal to be narrow-banded—hence it also referred to as the narrow-band approximation.
The slowly varying envelope approximation is often used because the resulting equations are in many cases easier to solve than the original equations, reducing the order of—all or some of—the highest-order partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s. But the validity of the assumptions which are made need to be justified.
Example
For example, consider the electromagnetic wave equationElectromagnetic wave equation
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
:
If k0 and ω0 are the wave number and angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of the (characteristic) carrier wave
Carrier wave
In telecommunications, a carrier wave or carrier is a waveform that is modulated with an input signal for the purpose of conveying information. This carrier wave is usually a much higher frequency than the input signal...
for the signal E(r,t), the following representation is useful:
where
denotes the real part of the quantity between brackets.In the slowly varying envelope approximation (SVEA) it is assumed that the complex-valued
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
E0(r, t) only varies slowly with r and t. This inherently implies that E0(r, t) represents waves propagating forward, predominantly in the k0 direction. As a result of the slow variation of E0(r, t), when taking derivatives, the highest-order derivatives may be neglected:
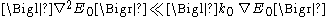and with 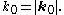Full approximation
Consequently, the wave equation is approximated in the SVEA as:It is convenient to choose k0 and ω0 such that they satisfy the dispersion relation
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
:
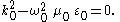
This gives the following approximation to the wave equation, as a result of the slowly varying envelope approximation:
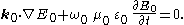
Which is a hyperbolic partial differential equation
Hyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
, like the original wave equation, but now of first-order instead of second-order. And valid for coherent forward-propagating waves in directions near the k0-direction.
Parabolic approximation
Assume wave propagation is dominantly in the z-direction, and k0 is taken in this direction. The SVEA is only applied to the second-order spatial derivatives in the z-direction and time. If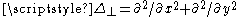 is the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
in the x–y plane, the result is:
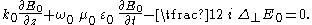
Which is a parabolic partial differential equation
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
. This equation has enhanced validity as compared to the full SVEA: it can represents waves propagating in directions significantly different from the z-direction.