Solder form
Encyclopedia
In mathematics
, more precisely in differential geometry, a soldering (or sometimes solder form) of a fibre bundle to a smooth manifold is a manner of attaching the fibres to the manifold in such a way that they can be regarded as tangent. Intuitively, soldering expresses in abstract terms the idea that a manifold may have a point of contact
with a certain model Klein geometry
at each point. In extrinsic differential geometry, the soldering is simply expressed by the tangency of the model space to the manifold. In intrinsic geometry, other techniques are needed to express it. Soldering was introduced in this general form by Charles Ehresmann
in 1950.
, and let E be a smooth fibre bundle over M with structure group G. Suppose that G acts transitively
on the typical fibre F of E, and that dim F = dim M. A soldering of E to M consists of the following data:
In particular, this latter condition can be interpreted as saying that θ determines a linear isomorphism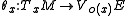
from the tangent space of M at x to the (vertical) tangent space of the fibre at the point determined by the distinguished section. The form θ is called the solder form for the soldering.
(a vector bundle without a choice of zero section). Then a soldering on E specifies first a distinguished section: that is, a choice of zero section o, so that E may be identified as a vector bundle. The solder form is then a linear isomorphism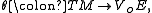
However, for a vector bundle there is a canonical isomorphism between the vertical space at the origin and the fibre VoE ≈ E. Making this identification, the solder form is specified by a linear isomorphism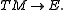
In other words, a soldering on an affine bundle E is a choice of isomorphism of E with the tangent bundle of M.
Often one speaks of a solder form on a vector bundle, where it is understood a priori that the distinguished section of the soldering is the zero section of the bundle. In this case, the structure group of the vector bundle is often implicitly enlarged by the semidirect product
of GL(n) with the typical fibre of E (which is a representation of GL(n)).
of a connection
.
P over a smooth manifold M is a horizontal and G-equivariant differential 1-form on P with values in a linear representation V of G such that the associated bundle map
from the tangent bundle
TM to the associated bundle
P×G V is a bundle isomorphism
. (In particular, V and M must have the same dimension.)
A motivating example of a solder form is the tautological or fundamental form on the frame bundle
of a manifold.
The reason for the name is that a solder form solders (or attaches) the abstract principal bundle to the manifold M by identifying an associated bundle with the tangent bundle. Solder forms provide a method for studying G-structures
and are important in the theory of Cartan connection
s. The terminology and approach is particularly popular in the physics literature.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more precisely in differential geometry, a soldering (or sometimes solder form) of a fibre bundle to a smooth manifold is a manner of attaching the fibres to the manifold in such a way that they can be regarded as tangent. Intuitively, soldering expresses in abstract terms the idea that a manifold may have a point of contact
Contact (mathematics)
In mathematics, contact of order k of functions is an equivalence relation, corresponding to having the same value at a point P and also the same derivatives there, up to order k. The equivalence classes are generally called jets...
with a certain model Klein geometry
Klein geometry
In mathematics, a Klein geometry is a type of geometry motivated by Felix Klein in his influential Erlangen program. More specifically, it is a homogeneous space X together with a transitive action on X by a Lie group G, which acts as the symmetry group of the geometry.For background and motivation...
at each point. In extrinsic differential geometry, the soldering is simply expressed by the tangency of the model space to the manifold. In intrinsic geometry, other techniques are needed to express it. Soldering was introduced in this general form by Charles Ehresmann
Charles Ehresmann
Charles Ehresmann was a French mathematician who worked on differential topology and category theory. He is known for work on the topology of Lie groups, the jet concept , and his seminar on category theory.He attended the École Normale Supérieure in Paris before performing one year of military...
in 1950.
Soldering of a fibre bundle
Let M be a smooth manifold, and G a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, and let E be a smooth fibre bundle over M with structure group G. Suppose that G acts transitively
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on the typical fibre F of E, and that dim F = dim M. A soldering of E to M consists of the following data:
- A distinguished sectionSection (fiber bundle)In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
o : M → E. - A linear isomorphism of vector bundles θ : TM → o-1VE from the tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of M to the pullbackPullback bundleIn mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
of the vertical bundleVertical bundleThe vertical bundle of a smooth fiber bundle is the subbundle of the tangent bundle that consists of all vectors which are tangent to the fibers...
of E along the distinguished section.
In particular, this latter condition can be interpreted as saying that θ determines a linear isomorphism
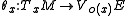
from the tangent space of M at x to the (vertical) tangent space of the fibre at the point determined by the distinguished section. The form θ is called the solder form for the soldering.
Affine bundles and vector bundles
Suppose that E is an affine vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
(a vector bundle without a choice of zero section). Then a soldering on E specifies first a distinguished section: that is, a choice of zero section o, so that E may be identified as a vector bundle. The solder form is then a linear isomorphism
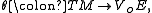
However, for a vector bundle there is a canonical isomorphism between the vertical space at the origin and the fibre VoE ≈ E. Making this identification, the solder form is specified by a linear isomorphism
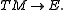
In other words, a soldering on an affine bundle E is a choice of isomorphism of E with the tangent bundle of M.
Often one speaks of a solder form on a vector bundle, where it is understood a priori that the distinguished section of the soldering is the zero section of the bundle. In this case, the structure group of the vector bundle is often implicitly enlarged by the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of GL(n) with the typical fibre of E (which is a representation of GL(n)).
Examples
- As a special case, for instance, the tangent bundle itself carries a canonical solder form, namely the identity.
- If M has a Riemannian metric (or pseudo-Riemannian metric), then the covariant metric tensor gives an isomorphism
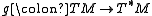from the tangent bundle to the cotangent bundleCotangent bundleIn mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
, which is a solder form.
Applications
A solder form on a vector bundle allows one to define the torsion tensorTorsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
of a connection
Connection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
.
Principal bundles
In the language of principal bundles, a solder form on a smooth principal G-bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
P over a smooth manifold M is a horizontal and G-equivariant differential 1-form on P with values in a linear representation V of G such that the associated bundle map
Bundle map
In mathematics, a bundle map is a morphism in the category of fiber bundles. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space. There are also several variations on the basic theme, depending on precisely...
from the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
TM to the associated bundle
Associated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
P×G V is a bundle isomorphism
Bundle map
In mathematics, a bundle map is a morphism in the category of fiber bundles. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space. There are also several variations on the basic theme, depending on precisely...
. (In particular, V and M must have the same dimension.)
A motivating example of a solder form is the tautological or fundamental form on the frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
of a manifold.
The reason for the name is that a solder form solders (or attaches) the abstract principal bundle to the manifold M by identifying an associated bundle with the tangent bundle. Solder forms provide a method for studying G-structures
G-structure
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
and are important in the theory of Cartan connection
Cartan connection
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
s. The terminology and approach is particularly popular in the physics literature.