
Sigma-finite measure
Encyclopedia
In mathematics
, a positive (or signed
) measure
μ defined on a σ-algebra
Σ of subsets of a set X is called finite if μ(X) is a finite real number
(rather than ∞). The measure μ is called σ-finite if X is the countable
union
of measurable sets of finite measure. A set in a measure space is said to have σ-finite measure if it is a countable union of sets with finite measure.
on the real number
s is not finite, but it is σ-finite. Indeed, consider the closed interval
s [k, k + 1] for all integer
s k; there are countably many such intervals, each has measure 1, and their union is the entire real line.
; the measure of any finite set is the number of elements in the set, and the measure of any infinite set is infinity. This measure is not σ-finite, because every set with finite measure contains only finitely many points, and it would take uncountably many such sets to cover the entire real line. But, the set of natural numbers with the counting measure
with the counting measure
is σ -finite.
s which are σ-compact are σ-finite under Haar measure
. For example, all connected
, locally compact groups G are σ-compact. To see this, let V be a relatively compact, symmetric (that is V = V−1) open neighborhood of the identity. Then

is an open subgroup of G. Therefore H is also closed since its complement is a union of open sets and by connectivity of G, must be G itself. Thus all connected Lie group
s are σ-finite under Haar measure.
 is clearly non σ-finite. One example in
is clearly non σ-finite. One example in 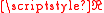 is: for all
is: for all 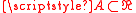 ,
,  if and only if A is not empty; another one is: for all
if and only if A is not empty; another one is: for all 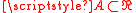 ,
, 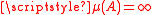 if and only if A is uncountable, 0 otherwise. Incidentally, both are translation-invariant.
if and only if A is uncountable, 0 otherwise. Incidentally, both are translation-invariant.
and Fubini's theorem
are invalid without an assumption of σ-finiteness (or something similar) on the measures involved.
Though measures which are not σ-finite are sometimes regarded as pathological, they do in fact occur quite naturally. For instance, if X is a metric space
of Hausdorff dimension
r, then all lower-dimensional Hausdorff measure
s are non-σ-finite if considered as measures on X.
to a probability measure
on X: let Vn, n ∈ N, be a covering of X by pairwise disjoint measurable sets of finite μ-measure, and let wn, n ∈ N, be a sequence of positive numbers (weights) such that
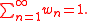
The measure ν defined by
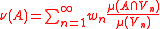
is then a probability measure on X with precisely the same null set
s as μ.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a positive (or signed
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
) measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
μ defined on a σ-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
Σ of subsets of a set X is called finite if μ(X) is a finite real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
(rather than ∞). The measure μ is called σ-finite if X is the countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of measurable sets of finite measure. A set in a measure space is said to have σ-finite measure if it is a countable union of sets with finite measure.
Lebesgue measure
For example, Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is not finite, but it is σ-finite. Indeed, consider the closed interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
s [k, k + 1] for all integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s k; there are countably many such intervals, each has measure 1, and their union is the entire real line.
Counting measure
Alternatively, consider the real numbers with the counting measureCounting measure
In mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
; the measure of any finite set is the number of elements in the set, and the measure of any infinite set is infinity. This measure is not σ-finite, because every set with finite measure contains only finitely many points, and it would take uncountably many such sets to cover the entire real line. But, the set of natural numbers
 with the counting measure
with the counting measureCounting measure
In mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
is σ -finite.
Locally compact groups
Locally compact groupLocally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
s which are σ-compact are σ-finite under Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
. For example, all connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, locally compact groups G are σ-compact. To see this, let V be a relatively compact, symmetric (that is V = V−1) open neighborhood of the identity. Then

is an open subgroup of G. Therefore H is also closed since its complement is a union of open sets and by connectivity of G, must be G itself. Thus all connected Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s are σ-finite under Haar measure.
Negative examples
Any measure taking only the two values 0 and is clearly non σ-finite. One example in
is clearly non σ-finite. One example in 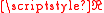 is: for all
is: for all 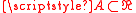 ,
,  if and only if A is not empty; another one is: for all
if and only if A is not empty; another one is: for all 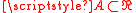 ,
, 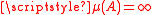 if and only if A is uncountable, 0 otherwise. Incidentally, both are translation-invariant.
if and only if A is uncountable, 0 otherwise. Incidentally, both are translation-invariant.Properties
The class of σ-finite measures has some very convenient properties; σ-finiteness can be compared in this respect to separability of topological spaces. Some theorems in analysis require σ-finiteness as a hypothesis. For example, both the Radon–Nikodym theoremRadon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
and Fubini's theorem
Fubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
are invalid without an assumption of σ-finiteness (or something similar) on the measures involved.
Though measures which are not σ-finite are sometimes regarded as pathological, they do in fact occur quite naturally. For instance, if X is a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
of Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
r, then all lower-dimensional Hausdorff measure
Hausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
s are non-σ-finite if considered as measures on X.
Equivalence to a probability measure
Any σ-finite measure μ on a space X is equivalentEquivalence (measure theory)
In mathematics, and specifically in measure theory, equivalence is a notion of two measures being "the same".-Definition:Let be a measurable space, and let μ, ν : Σ → R be two signed measures. Then μ is said to be equivalent to ν if and only if each is absolutely continuous with respect to the other...
to a probability measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on X: let Vn, n ∈ N, be a covering of X by pairwise disjoint measurable sets of finite μ-measure, and let wn, n ∈ N, be a sequence of positive numbers (weights) such that
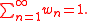
The measure ν defined by
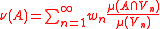
is then a probability measure on X with precisely the same null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
s as μ.

