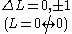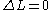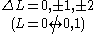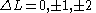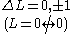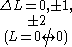Selection rule
Encyclopedia
In physics
and chemistry
a selection rule, or transition rule, formally constrains the possible transitions of a system from one state
to another. Selection rules have been derived for electronic, vibrational, and rotational transition
s. The selection rules may differ according to the technique used to observe the transition.
the basis for a spectroscopic selection rule is the value of the transition moment integral.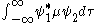
where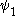 and
and 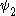 are the wave functions of the two states involved in the transition and µ is the transition moment operator. If the value of this integral is zero the transition is forbidden. In practice, the integral itself does not need to be calculated to determine a selection rule. It is sufficient to determine the symmetry
are the wave functions of the two states involved in the transition and µ is the transition moment operator. If the value of this integral is zero the transition is forbidden. In practice, the integral itself does not need to be calculated to determine a selection rule. It is sufficient to determine the symmetry
of transition moment function, . If the symmetry of this function spans the totally symmetric representation of the point group
. If the symmetry of this function spans the totally symmetric representation of the point group
to which the atom or molecule belongs then its value is not zero and the transition is allowed. Otherwise, the transition is forbidden.
To understand the role of symmetry in determining whether the value of a definite integral is zero or not zero, consider the integral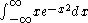
The function y=x e-x2 is plotted at the right. It has the same form as the wave function of the first excited state of a harmonic oscillator
. The (positive) area under the curve for x > 0 is equal to the (negative) area over the curve for x < 0. The sum of these two areas is zero; that is, the integral has a value of zero. This follows from the fact that the function is anti-symmetric in x; that is, y(-x) = -y(x). This argument can easily be extended to wave functions of more than one variable.
The transition moment integral is non-zero if and only if the transition moment function,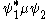 , is symmetric in at least one variable, as when y(x) = y(-x). The symmetry of the transition moment function is the direct product
, is symmetric in at least one variable, as when y(x) = y(-x). The symmetry of the transition moment function is the direct product
of the symmetries of its three components. The symmetry characteristics of each component can be obtained from standard character tables. Rules for obtaining the symmetries of a direct product can be found in texts on character tables.
is a selection rule formally-stated as follows: In a centrosymmetric environment transitions between like atomic orbitals such as s-s,p-p, d-d, or f-f transitions are forbidden. The Laporte rule applies to electric dipole transitions, so the operator has u symmetry. p orbitals also have u symmetry, so the symmetry of the transition moment function is given by the triple product
u×u×u, which has u symmetry. The transitions are therefore forbidden. Likewise, d orbitals have g symmetry, so the triple product g×u×g also has u symmetry and the transition is forbidden.
The wave function of a single electron is the product of a space-dependent wave function and a spin
wave function. Spin is directional and can be said to have odd parity
. It follows that transitions in which the spin "direction" changes are forbidden. In formal terms, only states with the same total spin quantum number are "spin-allowed". In crystal field theory
, d-d transitions that are spin-forbidden are very much weaker than spin-allowed transitions. Both can be observed, in spite of the Laporte rule, because the actual transitions are coupled to vibrations that are anti-symmetric and have the same symmetry as the dipole moment operator.
. In a fundamental vibration, the molecule is excited from its ground state
(v = 0) to the first excited state (v = 1). The symmetry of the ground-state wave function is the same as that of the molecule. It is, therefore, a basis for the totally symmetric representation in the point group
of the molecule. It follows that, for a vibrational transition to be allowed, the symmetry of the excited state wave function must be the same as the symmetry of the transition moment operator.
In infrared spectroscopy
, the transition moment operator transforms as either x and/or y and/or z. The excited state wave function must also transform as at least one of these vectors. In Raman spectroscopy
, the operator transforms as one of the second-order terms in the right-most column of the character
table, below.
The molecule methane, CH4, may be used as an example to illustrate the application of these principles. The molecule is tetrahedral and has Td symmetry. The vibrations of methane span the representations A1 + E + 2T2. Examination of the character table shows that all four vibrations are Raman-active, but only the T2 vibrations can be seen in the infrared spectrum.
In the harmonic approximation
, it can be shown that overtone
s are forbidden in both infrared and Raman spectra. However, when anharmonicity
is taken into account, the transitions are weakly allowed.
 There are many types of coupled transition such as are observed in vibration-rotation
There are many types of coupled transition such as are observed in vibration-rotation
spectra. The excited-state wave function is the product of two wave functions such as vibrational and rotational. The general principle is that the symmetry of the excited state is obtained as the direct product of the symmetries of the component wave functions. In rovibronic
transitions, the excited states involve three wave functions.
The infrared spectrum of hydrogen chloride
gas shows rotational fine structure superimposed on the vibrational spectrum. This is typical of the infrared spectra of heteronuclear diatomic molecules. It shows the so-called P and R branches. The Q branch, located at the vibration frequency, is absent. Symmetric top
molecules display the Q branch. This follows from the application of selection rules.
Resonance Raman spectroscopy
involves a kind of vibronic coupling. It results in much-increased intensity of fundamental and overtone transitions as the vibrations "steal" intensity from an allowed electronic transition. In spite of appearances, the selection rules are the same as in Raman spectroscopy.
In general, electric (charge) radiation or magnetic (current, magnetic moment radiation) can be classified into multipoles
Eλ (electric) or Mλ (magnetic) of order 2λ, e.g., E1 for electric dipole
, E2 for quadrupole
, or E3 for octupole. In transitions where the change in angular momentum between the initial and final states makes several multipole radiations possible, usually the lowest-order multipoles are overwhelmingly more likely, and dominate the transition.
The emitted particle carries away an angular momentum λ, which for the photon must be
at least 1, since it is a vector particle (i.e., it has JP
= 1-). Thus, there is no E0 (electric monopoles) or M0 (magnetic monopole
s, which do not seem to exist) radiation.
Since the total angular momentum has to be conserved during the transition, we have that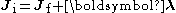
where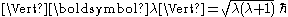 , and its z-projection is given by
, and its z-projection is given by  ;
; 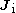 and
and 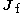 are, respectively, the initial and final angular momenta of the atom.
are, respectively, the initial and final angular momenta of the atom.
The corresponding quantum numbers λ, μ must satisfy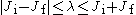
and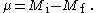
Parity is also preserved. For electric multipole transitions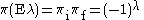
while for magnetic multipoles
Thus, parity does not change for E-even or M-odd multipoles, while it changes for E-odd or M-even multipoles.
These considerations generate different sets of transitions rules depending on the multipole order and type. The expression forbidden transitions is often used; this does not mean that these transitions cannot occur, only that they are electric-dipole-forbidden. These transitions are perfectly possible; they merely occur at a lower rate. If the rate for an E1 transition is non-zero, the transition is said to be permitted; if it is zero, then M1, E2, etc. transitions can still produce radiation, albeit with much lower transitions rates. These are the so-called forbidden transitions. The transition rate decreases by a factor of about 1000 from one multipole to the next one, so the lowest multipole transitions are most likely to occur.
Semi-forbidden transitions (resulting in so-called intercombination lines) are electric dipole (E1) transitions for which the selection rule that the spin does not change is violated. This is a result of the failure of LS coupling.
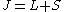 is the total angular momentum,
is the total angular momentum,
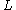 is the Azimuthal quantum number
is the Azimuthal quantum number
,
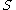 is the Spin quantum number
is the Spin quantum number
, and
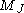 is the Magnetic quantum number
is the Magnetic quantum number
.
Which transitions are allowed is based on the Hydrogen-like atom
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
a selection rule, or transition rule, formally constrains the possible transitions of a system from one state
State of matter
States of matter are the distinct forms that different phases of matter take on. Solid, liquid and gas are the most common states of matter on Earth. However, much of the baryonic matter of the universe is in the form of hot plasma, both as rarefied interstellar medium and as dense...
to another. Selection rules have been derived for electronic, vibrational, and rotational transition
Rotational transition
A rotational transition is an abrupt change in angular momentum in quantum physics. Like all other properties of a quantum particle, angular momentum is quantized, meaning it can only equal certain discrete values, which correspond to different rotational energy states. When a particle loses...
s. The selection rules may differ according to the technique used to observe the transition.
Overview
In quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
the basis for a spectroscopic selection rule is the value of the transition moment integral.
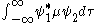
where
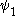 and
and 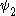 are the wave functions of the two states involved in the transition and µ is the transition moment operator. If the value of this integral is zero the transition is forbidden. In practice, the integral itself does not need to be calculated to determine a selection rule. It is sufficient to determine the symmetry
are the wave functions of the two states involved in the transition and µ is the transition moment operator. If the value of this integral is zero the transition is forbidden. In practice, the integral itself does not need to be calculated to determine a selection rule. It is sufficient to determine the symmetrySymmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of transition moment function,
 . If the symmetry of this function spans the totally symmetric representation of the point group
. If the symmetry of this function spans the totally symmetric representation of the point groupPoint group
In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
to which the atom or molecule belongs then its value is not zero and the transition is allowed. Otherwise, the transition is forbidden.
To understand the role of symmetry in determining whether the value of a definite integral is zero or not zero, consider the integral
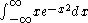
The function y=x e-x2 is plotted at the right. It has the same form as the wave function of the first excited state of a harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
. The (positive) area under the curve for x > 0 is equal to the (negative) area over the curve for x < 0. The sum of these two areas is zero; that is, the integral has a value of zero. This follows from the fact that the function is anti-symmetric in x; that is, y(-x) = -y(x). This argument can easily be extended to wave functions of more than one variable.
The transition moment integral is non-zero if and only if the transition moment function,
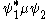 , is symmetric in at least one variable, as when y(x) = y(-x). The symmetry of the transition moment function is the direct product
, is symmetric in at least one variable, as when y(x) = y(-x). The symmetry of the transition moment function is the direct productDirect product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of the symmetries of its three components. The symmetry characteristics of each component can be obtained from standard character tables. Rules for obtaining the symmetries of a direct product can be found in texts on character tables.
| Transition type | µ transforms as | note |
|---|---|---|
| Electric dipole | x, y, z | Optical spectra |
| Electric quadrupole | x2, y2, z2, xy, xz, yz | Constraint x2 + y2 + z2 = 0 |
| Electric polarizability | x2, y2, z2, xy, xz, yz | Raman spectra |
| Magnetic dipole | Rx, Ry, Rz | Optical spectra (weak) |
Electronic spectra
The Laporte ruleLaporte rule
The Laporte rule is a spectroscopic selection rule. It states that electronic transitions that conserve either symmetry or asymmetry with respect to an inversion center — i.e., g → g, or u → u respectively—are forbidden...
is a selection rule formally-stated as follows: In a centrosymmetric environment transitions between like atomic orbitals such as s-s,p-p, d-d, or f-f transitions are forbidden. The Laporte rule applies to electric dipole transitions, so the operator has u symmetry. p orbitals also have u symmetry, so the symmetry of the transition moment function is given by the triple product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
u×u×u, which has u symmetry. The transitions are therefore forbidden. Likewise, d orbitals have g symmetry, so the triple product g×u×g also has u symmetry and the transition is forbidden.
The wave function of a single electron is the product of a space-dependent wave function and a spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
wave function. Spin is directional and can be said to have odd parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
. It follows that transitions in which the spin "direction" changes are forbidden. In formal terms, only states with the same total spin quantum number are "spin-allowed". In crystal field theory
Crystal field theory
Crystal field theory is a model that describes the electronic structure of transition metal compounds, all of which can be considered coordination complexes. CFT successfully accounts for some magnetic properties, colours, hydration enthalpies, and spinel structures of transition metal complexes,...
, d-d transitions that are spin-forbidden are very much weaker than spin-allowed transitions. Both can be observed, in spite of the Laporte rule, because the actual transitions are coupled to vibrations that are anti-symmetric and have the same symmetry as the dipole moment operator.
Vibrational spectra
In vibrational spectroscopy, transitions are observed between different vibrational statesMolecular vibration
A molecular vibration occurs when atoms in a molecule are in periodic motion while the molecule as a whole has constant translational and rotational motion...
. In a fundamental vibration, the molecule is excited from its ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
(v = 0) to the first excited state (v = 1). The symmetry of the ground-state wave function is the same as that of the molecule. It is, therefore, a basis for the totally symmetric representation in the point group
Point group
In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
of the molecule. It follows that, for a vibrational transition to be allowed, the symmetry of the excited state wave function must be the same as the symmetry of the transition moment operator.
In infrared spectroscopy
Infrared spectroscopy
Infrared spectroscopy is the spectroscopy that deals with the infrared region of the electromagnetic spectrum, that is light with a longer wavelength and lower frequency than visible light. It covers a range of techniques, mostly based on absorption spectroscopy. As with all spectroscopic...
, the transition moment operator transforms as either x and/or y and/or z. The excited state wave function must also transform as at least one of these vectors. In Raman spectroscopy
Raman spectroscopy
Raman spectroscopy is a spectroscopic technique used to study vibrational, rotational, and other low-frequency modes in a system.It relies on inelastic scattering, or Raman scattering, of monochromatic light, usually from a laser in the visible, near infrared, or near ultraviolet range...
, the operator transforms as one of the second-order terms in the right-most column of the character
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
table, below.
| E | 8 C3 | 3 C2 | 6 S4 | 6 σd | >- | 1 | 1 | 1 | 1 | 1 | > x2 + y2 + z2 | 1 | 1 | 1 | -1 | -1 | >- | 2 | -1 | 2 | 0 | 0 | > (2 z2 - x2 - y2,x2 - y2) | 3 | 0 | -1 | 1 | > (Rx, Ry, Rz) | >- | 3 | 0 | -1 | -1 | > (x, y, z) |
The molecule methane, CH4, may be used as an example to illustrate the application of these principles. The molecule is tetrahedral and has Td symmetry. The vibrations of methane span the representations A1 + E + 2T2. Examination of the character table shows that all four vibrations are Raman-active, but only the T2 vibrations can be seen in the infrared spectrum.
In the harmonic approximation
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
, it can be shown that overtone
Overtone
An overtone is any frequency higher than the fundamental frequency of a sound. The fundamental and the overtones together are called partials. Harmonics are partials whose frequencies are whole number multiples of the fundamental These overlapping terms are variously used when discussing the...
s are forbidden in both infrared and Raman spectra. However, when anharmonicity
Anharmonicity
In classical mechanics, anharmonicity is the deviation of a system from being a harmonic oscillator. An oscillator that is not oscillating in simple harmonic motion is known as an anharmonic oscillator where the system can be approximated to a harmonic oscillator and the anharmonicity can be...
is taken into account, the transitions are weakly allowed.
Rotational spectra
The selection rule for rotational transitions, derived from the symmetries of the rotational wave functions in a rigid rotor, is ΔJ = ±1, where J is a rotational quantum number.Coupled transitions

Rovibrational coupling
Rovibrational coupling is a coupled rotational and vibrational excitation of a molecule. It is different from rovibronic coupling, which involves a change in all of electronic, vibrational, and rotational states simultaneously....
spectra. The excited-state wave function is the product of two wave functions such as vibrational and rotational. The general principle is that the symmetry of the excited state is obtained as the direct product of the symmetries of the component wave functions. In rovibronic
Rovibronic coupling
Rovibronic coupling denotes the simultaneous interactions between rotational, vibrational, and electronic degrees of freedom in a molecule. When a rovibronic transition occurs, the rotational, vibrational, and electronic states change simultaneously, unlike in rovibrational coupling...
transitions, the excited states involve three wave functions.
The infrared spectrum of hydrogen chloride
Hydrogen chloride
The compound hydrogen chloride has the formula HCl. At room temperature, it is a colorless gas, which forms white fumes of hydrochloric acid upon contact with atmospheric humidity. Hydrogen chloride gas and hydrochloric acid are important in technology and industry...
gas shows rotational fine structure superimposed on the vibrational spectrum. This is typical of the infrared spectra of heteronuclear diatomic molecules. It shows the so-called P and R branches. The Q branch, located at the vibration frequency, is absent. Symmetric top
Rotational spectroscopy
Rotational spectroscopy or microwave spectroscopy studies the absorption and emission of electromagnetic radiation by molecules associated with a corresponding change in the rotational quantum number of the molecule...
molecules display the Q branch. This follows from the application of selection rules.
Resonance Raman spectroscopy
Resonance Raman spectroscopy
Resonance Raman spectroscopy is a specialized implementation of the more general Raman spectroscopy.- Overview :As in Raman spectroscopy, RR spectroscopy provides information about the vibrations of molecules, and can also be used for identifying unknown substances. RR spectroscopy has found wide...
involves a kind of vibronic coupling. It results in much-increased intensity of fundamental and overtone transitions as the vibrations "steal" intensity from an allowed electronic transition. In spite of appearances, the selection rules are the same as in Raman spectroscopy.
Angular momentum
- See also angular momentum couplingAngular momentum couplingIn quantum mechanics, the procedure of constructing eigenstates of total angular momentum out of eigenstates of separate angular momenta is called angular momentum coupling. For instance, the orbit and spin of a single particle can interact through spin-orbit interaction, in which case the...
In general, electric (charge) radiation or magnetic (current, magnetic moment radiation) can be classified into multipoles
Multipole moments
In mathematics, especially as applied to physics, multipole moments are the coefficients of a series expansion of a potential due to continuous or discrete sources . A multipole moment usually involves powers of the distance to the origin, as well as some angular dependence...
Eλ (electric) or Mλ (magnetic) of order 2λ, e.g., E1 for electric dipole
Dipole
In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
, E2 for quadrupole
Quadrupole
A quadrupole or quadrapole is one of a sequence of configurations of—for example—electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.-Mathematical...
, or E3 for octupole. In transitions where the change in angular momentum between the initial and final states makes several multipole radiations possible, usually the lowest-order multipoles are overwhelmingly more likely, and dominate the transition.
The emitted particle carries away an angular momentum λ, which for the photon must be
at least 1, since it is a vector particle (i.e., it has JP
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
= 1-). Thus, there is no E0 (electric monopoles) or M0 (magnetic monopole
Magnetic monopole
A magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
s, which do not seem to exist) radiation.
Since the total angular momentum has to be conserved during the transition, we have that
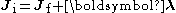
where
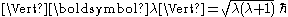 , and its z-projection is given by
, and its z-projection is given by  ;
; 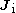 and
and 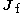 are, respectively, the initial and final angular momenta of the atom.
are, respectively, the initial and final angular momenta of the atom.The corresponding quantum numbers λ, μ must satisfy
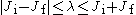
and
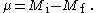
Parity is also preserved. For electric multipole transitions
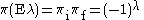
while for magnetic multipoles

Thus, parity does not change for E-even or M-odd multipoles, while it changes for E-odd or M-even multipoles.
These considerations generate different sets of transitions rules depending on the multipole order and type. The expression forbidden transitions is often used; this does not mean that these transitions cannot occur, only that they are electric-dipole-forbidden. These transitions are perfectly possible; they merely occur at a lower rate. If the rate for an E1 transition is non-zero, the transition is said to be permitted; if it is zero, then M1, E2, etc. transitions can still produce radiation, albeit with much lower transitions rates. These are the so-called forbidden transitions. The transition rate decreases by a factor of about 1000 from one multipole to the next one, so the lowest multipole transitions are most likely to occur.
Semi-forbidden transitions (resulting in so-called intercombination lines) are electric dipole (E1) transitions for which the selection rule that the spin does not change is violated. This is a result of the failure of LS coupling.
Summary table
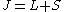 is the total angular momentum,
is the total angular momentum,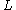 is the Azimuthal quantum number
is the Azimuthal quantum numberAzimuthal quantum number
The azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital...
,
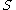 is the Spin quantum number
is the Spin quantum numberSpin quantum number
In atomic physics, the spin quantum number is a quantum number that parameterizes the intrinsic angular momentum of a given particle...
, and
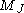 is the Magnetic quantum number
is the Magnetic quantum numberMagnetic quantum number
In atomic physics, the magnetic quantum number is the third of a set of quantum numbers which describe the unique quantum state of an electron and is designated by the letter m...
.
Which transitions are allowed is based on the Hydrogen-like atom
Hydrogen-like atom
A hydrogen-like ion is any atomic nucleus with one electron and thus is isoelectronic with hydrogen. Except for the hydrogen atom itself , these ions carry the positive charge e, where Z is the atomic number of the atom. Examples of hydrogen-like ions are He+, Li2+, Be3+ and B4+...
.
| Electric dipole (E1) | Magnetic dipole (M1) | Electric quadrupole (E2) | Magnetic quadrupole (M2) | Electric octupole (E3) | Magnetic octupole (M3) | ||
|---|---|---|---|---|---|---|---|
| Rigorous rules | (1) | 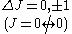 |
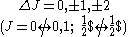 |
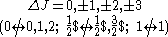 |
|||
| (2) | 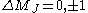 |
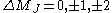 |
 |
||||
| (3) |  |
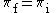 |
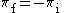 |
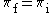 |
|||
| LS coupling | (4) | One electron jump Δl = ±1 |
No electron jump Δl = 0, |
None or one electron jump Δl = 0, ±2 |
One electron jump Δl = ±1 |
One electron jump Δl = ±1, ±3 |
One electron jump Δl = 0, ±2 |
| (5) | If ΔS = 0
|
If ΔS = 0
|
If ΔS = 0
|
If ΔS = 0
|
|||
| Intermediate coupling | (6) | If ΔS = ±1
|
If ΔS = ±1
|
If ΔS = ±1
|
If ΔS = ±1
|
If ΔS = ±1
|
|