Anharmonicity
Encyclopedia
In classical mechanics
, anharmonicity is the deviation of a system from being a harmonic oscillator
. An oscillator that is not oscillating in simple harmonic motion
is known as an anharmonic oscillator where the system can be approximated to a harmonic oscillator and the anharmonicity can be calculated using perturbation theory
. If the anharmonicity is large then other numerical techniques
have to be used.
As a result, oscillations with frequencies
and 
etc., where 
is the fundamental frequency of the oscillator, appear. Furthermore, the frequency 
deviates from the frequency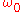 
of the harmonic oscillations. As a first approximation, the frequency shift 
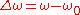is proportional to the square of the oscillation amplitude 
:
In a system of oscillators with natural frequencies
, 
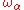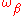, ... anharmonicity results in additional oscillations with frequencies 
.
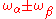Anharmonicity also modifies the profile of the resonance curve, leading to interesting phenomena such as the foldover effect
and superharmonic resonance.
In a mechanical anharmonic oscillator, the relationship between force and displacement is not linear but depends upon the amplitude of the displacement. The nonlinearity arises from the fact that the spring is not capable of exerting a restoring force that is proportional to its displacement because of, for example, stretching in the material comprising the spring. As a result of the nonlinearity, the vibration frequency can change, depending upon the system's displacement. These changes in the vibration frequency result in energy being coupled from the fundamental vibration frequency to other frequencies through a process known as parametric coupling.
Further examples of anharmonic oscillators include the large-angle pendulum, which exhibits chaotic behavior as a result of its anharmonicity; nonequilibrium semiconductors that possess a large hot carrier population, which exhibit nonlinear behaviors of various types related to the effective mass of the carriers; and ionospheric plasmas, which also exhibit nonlinear behavior based on the anharmonicity of the plasma. In fact, virtually all oscillators become anharmonic when their pump amplitude increases beyond some threshold, and as a result it is necessary to use nonlinear equations of motion to describe their behavior.
Anharmonicity plays a role in lattice and molecular vibrations, in quantum oscillations http://jchemed.chem.wisc.edu/Journal/issues/2005/Aug/abs1263_2.html, and in Acoustics
.
.
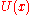Assuming that the curve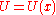
is symmetric about the 
-axis, the shape of the curve can be implicitly determined from the period 
of the oscillations of particles with energy 
according to the formula:
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, anharmonicity is the deviation of a system from being a harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
. An oscillator that is not oscillating in simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
is known as an anharmonic oscillator where the system can be approximated to a harmonic oscillator and the anharmonicity can be calculated using perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
. If the anharmonicity is large then other numerical techniques
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
have to be used.
As a result, oscillations with frequencies
and etc., where is the fundamental frequency of the oscillator, appear. Furthermore, the frequency deviates from the frequency 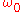of the harmonic oscillations. As a first approximation, the frequency shift 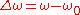is proportional to the square of the oscillation amplitude :In a system of oscillators with natural frequencies
Normal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
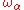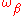, , ... anharmonicity results in additional oscillations with frequencies 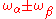.Anharmonicity also modifies the profile of the resonance curve, leading to interesting phenomena such as the foldover effect
Nonlinear resonance
In physics, nonlinear resonance is the occurrence of resonance in a nonlinear system. In nonlinear resonance the system behaviour – resonance frequencies and modes – depends on the amplitude of the oscillations, while for linear systems this is independent of amplitude.-Description:Generically two...
and superharmonic resonance.
General principle
A generalized version of harmonic oscillator in which the relationship between force and displacement is linear. The harmonic oscillator is a highly idealized system that oscillates with a single frequency, irrespective of the amount of pumping or energy injected into the system. Consequently, the harmonic oscillator's fundamental frequency of vibration is independent of the amplitude of the vibrations. Applications of the harmonic oscillator model abound in various fields, but perhaps the most commonly studied system is the Hooke's law mass-spring system. In the Hooke's law system the restoring force exerted on the mass is proportional to the displacement of the mass from its equilibrium position. This linear relationship between force and displacement mandates that the oscillation frequency of the mass will be independent of the amplitude of the displacement.In a mechanical anharmonic oscillator, the relationship between force and displacement is not linear but depends upon the amplitude of the displacement. The nonlinearity arises from the fact that the spring is not capable of exerting a restoring force that is proportional to its displacement because of, for example, stretching in the material comprising the spring. As a result of the nonlinearity, the vibration frequency can change, depending upon the system's displacement. These changes in the vibration frequency result in energy being coupled from the fundamental vibration frequency to other frequencies through a process known as parametric coupling.
Examples in physics
There are many systems throughout the physical world that can be modeled as anharmonic oscillators in addition to the nonlinear mass-spring system. For example, an atom, which consists of a positively charged nucleus surrounded by a negatively charged electronic cloud, experiences a displacement between the center of mass of the nucleus and the electronic cloud when an electric field is present. The amount of that displacement, called the electric dipole moment, is related linearly to the applied field for small fields, but as the magnitude of the field is increased, the field-dipole moment relationship becomes nonlinear, just as in the mechanical system.Further examples of anharmonic oscillators include the large-angle pendulum, which exhibits chaotic behavior as a result of its anharmonicity; nonequilibrium semiconductors that possess a large hot carrier population, which exhibit nonlinear behaviors of various types related to the effective mass of the carriers; and ionospheric plasmas, which also exhibit nonlinear behavior based on the anharmonicity of the plasma. In fact, virtually all oscillators become anharmonic when their pump amplitude increases beyond some threshold, and as a result it is necessary to use nonlinear equations of motion to describe their behavior.
Anharmonicity plays a role in lattice and molecular vibrations, in quantum oscillations http://jchemed.chem.wisc.edu/Journal/issues/2005/Aug/abs1263_2.html, and in Acoustics
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
.
Potential energy from period of oscillations
Let us consider a potential well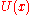.Assuming that the curve
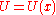is symmetric about the -axis, the shape of the curve can be implicitly determined from the period of the oscillations of particles with energy according to the formula:See also
- InharmonicityInharmonicityIn music, inharmonicity is the degree to which the frequencies of overtones depart from whole multiples of the fundamental frequency....
- Harmonic oscillatorHarmonic oscillatorIn classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
- Quantum harmonic oscillatorQuantum harmonic oscillatorThe quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
- Musical acousticsMusical acousticsMusical acoustics or music acoustics is the branch of acoustics concerned with researching and describing the physics of music – how sounds employed as music work...
- Nonlinear resonanceNonlinear resonanceIn physics, nonlinear resonance is the occurrence of resonance in a nonlinear system. In nonlinear resonance the system behaviour – resonance frequencies and modes – depends on the amplitude of the oscillations, while for linear systems this is independent of amplitude.-Description:Generically two...