
Molecular vibration
Encyclopedia
A molecular vibration occurs when atoms in a molecule
are in periodic motion
while the molecule as a whole has constant translational and rotational motion. The frequency of the periodic motion is known as a vibration frequency, and the typical frequencies of molecular vibrations range from less than 1012 to approximately 1014 Hz.
In general, a molecule with N atoms has 3N – 6 normal modes of vibration, but a linear molecule has 3N – 5 such modes, as rotation about its molecular axis cannot be observed. A diatomic molecule has one normal mode of vibration. The normal modes of vibration of polyatomic molecules are independent of each other but each normal mode will involve simultaneous vibrations of different parts of the molecule such as different chemical bonds.
A molecular vibration is excited when the molecule absorbs a quantum of energy, E, corresponding to the vibration's frequency, ν, according to the relation E = hν (where h is Planck's constant
). A fundamental vibration is excited when one such quantum of energy is absorbed by the molecule in its ground state
. When two quanta are absorbed the first overtone
is excited, and so on to higher overtones.
To a first approximation, the motion in a normal vibration can be described as a kind of simple harmonic motion
. In this approximation, the vibrational energy is a quadratic function (parabola) with respect to the atomic displacements and the first overtone has twice the frequency of the fundamental. In reality, vibrations are anharmonic
and the first overtone has a frequency that is slightly lower than twice that of the fundamental. Excitation of the higher overtones involves progressively less and less additional energy and eventually leads to dissociation of the molecule, as the potential energy of the molecule is more like a Morse potential
.
The vibrational states of a molecule can be probed in a variety of ways. The most direct way is through infrared spectroscopy
, as vibrational transitions typically require an amount of energy that corresponds to the infrared region of the spectrum. Raman spectroscopy
, which typically uses visible light, can also be used to measure vibration frequencies directly.
Vibrational excitation can occur in conjunction with electronic excitation (vibronic transition
), giving vibrational fine structure to electronic transitions, particularly with molecules in the gas state.
Simultaneous excitation of a vibration and rotations gives rise to vibration-rotation
spectra.
,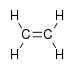
In a rocking, wagging or twisting coordinate the bond lengths within the groups involved do not change. The angles do. Rocking is distinguished from wagging by the fact that the atoms in the group stay in the same plane.
In ethene there are 12 internal coordinates: 4 C-H stretching, 1 C-C stretching, 2 H-C-H bending, 2 CH2 rocking, 2 CH2 wagging, 1 twisting. Note that the H-C-C angles cannot be used as internal coordinates as the angles at each carbon atom cannot all increase at the same time.
s, can vibrate in six different ways: symmetric and antisymmetric stretching, scissoring, rocking, wagging and twisting as shown here:
(These figures do not represent the "recoil
" of the C atoms, which, though necessarily present to balance the overall movements of the molecule, are much smaller than the movements of the lighter H atoms).
of the molecular point group
. For example, the four(un-normalised) C-H stretching coordinates of the molecule ethene are given by
where q1 - q4 are the internal coordinates for stretching of each of the four C-H bonds.
Illustrations of symmetry-adapted coordinates for most small molecules can be found in Nakamoto.
, and the normal modes will "transform as" an irreducible representation under that group. The normal modes can then be qualitatively determined by applying group theory and projecting the irreducible representation onto the cartesian coordinates. For example, when this treatment is applied to CO2, it is found that the C=O stretches are not independent, but rather there is a O=C=O symmetric stretch and an O=C=O asymmetric stretch.
When two or more normal coordinates belong to the same irreducible representation of the molecular point group (colloquially, have the same symmetry) there is "mixing" and the coefficients of the combination cannot be determined a priori. For example, in the linear molecule hydrogen cyanide, HCN, The two stretching vibrations are
The coefficients a and b are found by performing a full normal coordinate analysis by means of the Wilson GF method
.
: the force required to extend the spring is proportional to the extension. The proportionality constant is known as a force constant, k. The anharmonic oscillator is considered elsewhere.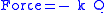
By Newton’s second law of motion
this force is also equal to a reduced mass
, μ, times acceleration.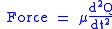
Since this is one and the same force the ordinary differential equation
follows.
The solution to this equation of simple harmonic motion
is
A is the maximum amplitude of the vibration coordinate Q. It remains to define the reduced mass, μ. In general, the reduced mass of a diatomic molecule, AB, is expressed in terms of the atomic masses, mA and mB, as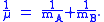
The use of the reduced mass ensures that the centre of mass of the molecule is not affected by the vibration. In the harmonic approximation the potential energy of the molecule is a quadratic function of the normal coordinate. It follows that the force-constant is equal to the second derivative of the potential energy.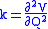
When two or more normal vibrations have the same symmetry a full normal coordinate analysis must be performed (see GF method
). The vibration frequencies,νi are obtained from the eigenvalues,λi, of the matrix product GF. G is a matrix of numbers derived from the masses of the atoms and the geometry of the molecule. F is a matrix derived from force-constant values. Details concerning the determination of the eigenvalues can be found in.
 ,
,
where n is a quantum number that can take values of 0, 1, 2 ... The difference in energy when n changes by 1 are therefore equal to the energy derived using classical mechanics. See quantum harmonic oscillator
for graphs of the first 5 wave functions.
Knowing the wave functions, certain selection rules can be formulated. For example, for a harmonic oscillator transitions are allowed only when the quantum number n changes by one,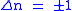
but this does not apply to an anharmonic oscillator; the observation of overtones is only possible because vibrations are anharmonic. Another consequence of anharmonicity is that transitions such as between states n=2 and n=1 have slightly less energy than transitions between the ground state and first excited state. Such a transition gives rise to a hot band
.
of an absorption band is proportional to the derivative of the molecular dipole moment with respect to the normal coordinate. The intensity of Raman bands depends on polarizability
.
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
are in periodic motion
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
while the molecule as a whole has constant translational and rotational motion. The frequency of the periodic motion is known as a vibration frequency, and the typical frequencies of molecular vibrations range from less than 1012 to approximately 1014 Hz.
In general, a molecule with N atoms has 3N – 6 normal modes of vibration, but a linear molecule has 3N – 5 such modes, as rotation about its molecular axis cannot be observed. A diatomic molecule has one normal mode of vibration. The normal modes of vibration of polyatomic molecules are independent of each other but each normal mode will involve simultaneous vibrations of different parts of the molecule such as different chemical bonds.
A molecular vibration is excited when the molecule absorbs a quantum of energy, E, corresponding to the vibration's frequency, ν, according to the relation E = hν (where h is Planck's constant
Planck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
). A fundamental vibration is excited when one such quantum of energy is absorbed by the molecule in its ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
. When two quanta are absorbed the first overtone
Overtone
An overtone is any frequency higher than the fundamental frequency of a sound. The fundamental and the overtones together are called partials. Harmonics are partials whose frequencies are whole number multiples of the fundamental These overlapping terms are variously used when discussing the...
is excited, and so on to higher overtones.
To a first approximation, the motion in a normal vibration can be described as a kind of simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
. In this approximation, the vibrational energy is a quadratic function (parabola) with respect to the atomic displacements and the first overtone has twice the frequency of the fundamental. In reality, vibrations are anharmonic
Anharmonicity
In classical mechanics, anharmonicity is the deviation of a system from being a harmonic oscillator. An oscillator that is not oscillating in simple harmonic motion is known as an anharmonic oscillator where the system can be approximated to a harmonic oscillator and the anharmonicity can be...
and the first overtone has a frequency that is slightly lower than twice that of the fundamental. Excitation of the higher overtones involves progressively less and less additional energy and eventually leads to dissociation of the molecule, as the potential energy of the molecule is more like a Morse potential
Morse potential
The Morse potential, named after physicist Philip M. Morse, is a convenient model for the potential energy of a diatomic molecule. It is a better approximation for the vibrational structure of the molecule than the quantum harmonic oscillator because it explicitly includes the effects of bond...
.
The vibrational states of a molecule can be probed in a variety of ways. The most direct way is through infrared spectroscopy
Infrared spectroscopy
Infrared spectroscopy is the spectroscopy that deals with the infrared region of the electromagnetic spectrum, that is light with a longer wavelength and lower frequency than visible light. It covers a range of techniques, mostly based on absorption spectroscopy. As with all spectroscopic...
, as vibrational transitions typically require an amount of energy that corresponds to the infrared region of the spectrum. Raman spectroscopy
Raman spectroscopy
Raman spectroscopy is a spectroscopic technique used to study vibrational, rotational, and other low-frequency modes in a system.It relies on inelastic scattering, or Raman scattering, of monochromatic light, usually from a laser in the visible, near infrared, or near ultraviolet range...
, which typically uses visible light, can also be used to measure vibration frequencies directly.
Vibrational excitation can occur in conjunction with electronic excitation (vibronic transition
Vibronic transition
A vibronic transition denotes the simultaneous change of vibrational and electronic quantum number in a molecule. According to the separability of electronic and nuclear motion in the Born-Oppenheimer approximation, the vibrational transition and electronic transition may be described separately...
), giving vibrational fine structure to electronic transitions, particularly with molecules in the gas state.
Simultaneous excitation of a vibration and rotations gives rise to vibration-rotation
Rovibrational coupling
Rovibrational coupling is a coupled rotational and vibrational excitation of a molecule. It is different from rovibronic coupling, which involves a change in all of electronic, vibrational, and rotational states simultaneously....
spectra.
Vibrational coordinates
The coordinate of a normal vibration is a combination of changes in the positions of atoms in the molecule. When the vibration is excited the coordinate changes sinusoidally with a frequency ν, the frequency of the vibration.Internal coordinates
Internal coordinates are of the following types, illustrated with reference to the planar molecule ethyleneEthylene
Ethylene is a gaseous organic compound with the formula . It is the simplest alkene . Because it contains a carbon-carbon double bond, ethylene is classified as an unsaturated hydrocarbon. Ethylene is widely used in industry and is also a plant hormone...
,

- Stretching: a change in the length of a bond, such as C-H or C-C
- Bending: a change in the angle between two bonds, such as the HCH angle in a methylene group
- Rocking: a change in angle between a group of atoms, such as a methylene group and the rest of the molecule.
- Wagging: a change in angle between the plane of a group of atoms, such as a methylene group and a plane through the rest of the molecule,
- Twisting: a change in the angle between the planes of two groups of atoms, such as a change in the angle between the two methylene groups.
- Out-of-plane: a change in the angle between any one of the C-H bonds and the plane defined by the remaining atoms of the ethylene molecule. Another example is in BF3 when the boron atom moves in and out of the plane of the three fluorine atoms.
In a rocking, wagging or twisting coordinate the bond lengths within the groups involved do not change. The angles do. Rocking is distinguished from wagging by the fact that the atoms in the group stay in the same plane.
In ethene there are 12 internal coordinates: 4 C-H stretching, 1 C-C stretching, 2 H-C-H bending, 2 CH2 rocking, 2 CH2 wagging, 1 twisting. Note that the H-C-C angles cannot be used as internal coordinates as the angles at each carbon atom cannot all increase at the same time.
Vibrations of a Methylene group (-CH2-) in a molecule for illustration
The atoms in a CH2 group, commonly found in organic compoundOrganic compound
An organic compound is any member of a large class of gaseous, liquid, or solid chemical compounds whose molecules contain carbon. For historical reasons discussed below, a few types of carbon-containing compounds such as carbides, carbonates, simple oxides of carbon, and cyanides, as well as the...
s, can vibrate in six different ways: symmetric and antisymmetric stretching, scissoring, rocking, wagging and twisting as shown here:
| Symmetrical stretching |
Antisymmetrical stretching |
Bending |
|---|---|---|
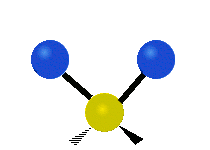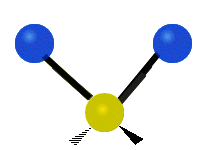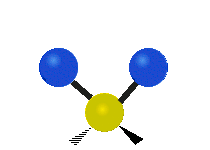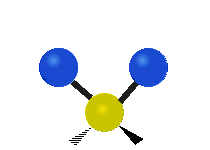 |
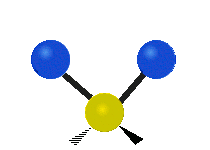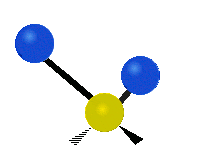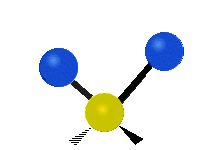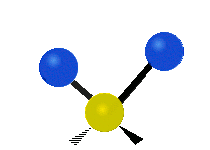 |
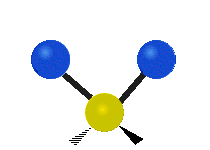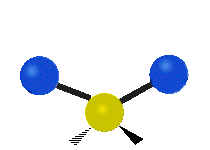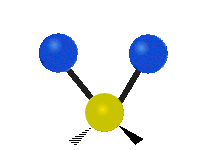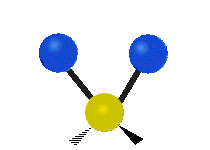 |
| Rocking | Wagging | Twisting |
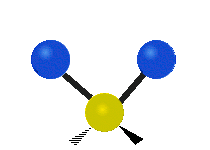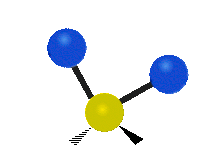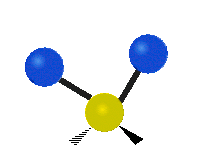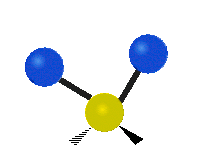 |
 |
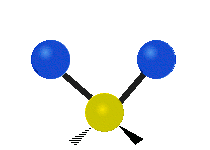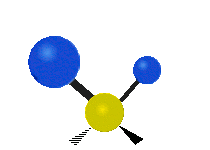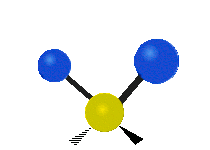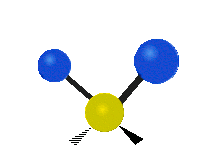 |
(These figures do not represent the "recoil
Recoil
Recoil is the backward momentum of a gun when it is discharged. In technical terms, the recoil caused by the gun exactly balances the forward momentum of the projectile and exhaust gasses, according to Newton's third law...
" of the C atoms, which, though necessarily present to balance the overall movements of the molecule, are much smaller than the movements of the lighter H atoms).
Symmetry-adapted coordinates
Symmetry-adapted coordinates may be created by applying a projection operator to a set of internal coordinates. The projection operator is constructed with the aid of the character tableCharacter table
In group theory, a character table is a two-dimensional table whose rows correspond to irreducible group representations, and whose columns correspond to classes of group elements...
of the molecular point group
Point group
In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
. For example, the four(un-normalised) C-H stretching coordinates of the molecule ethene are given by
- Qs1 = q1 + q2 + q3 + q4
- Qs2 = q1 + q2 - q3 - q4
- Qs3 = q1 - q2 + q3 - q4
- Qs4 = q1 - q2 - q3 + q4
where q1 - q4 are the internal coordinates for stretching of each of the four C-H bonds.
Illustrations of symmetry-adapted coordinates for most small molecules can be found in Nakamoto.
Normal coordinates
The normal coordinates, denoted as Q, refer to the positions of atoms away from their equilibrium positions, with respect to a normal mode of vibration. Each normal mode is assigned a single normal coordinate, and so the normal coordinate refers to the "progress" along that normal mode at any given time. Formally, normal modes are determined by solving a secular determinant, and then the normal coordinates (over the normal modes) can be expressed as a summation over the cartesian cordinates (over the atom positions). The advantage of working in normal modes is that they diagonalize the matrix governing the molecular vibrations, so each normal mode is an independent molecular vibration, associated with its own spectrum of quantum mechanical states. If the molecule possesses symmetries, it will belong to a point groupPoint group
In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
, and the normal modes will "transform as" an irreducible representation under that group. The normal modes can then be qualitatively determined by applying group theory and projecting the irreducible representation onto the cartesian coordinates. For example, when this treatment is applied to CO2, it is found that the C=O stretches are not independent, but rather there is a O=C=O symmetric stretch and an O=C=O asymmetric stretch.
- symmetric stretching: the sum of the two C-O stretching coordinates; the two C-O bond lengths change by the same amount and the carbon atom is stationary. Q = q1 + q2
- asymmetric stretching: the difference of the two C-O stretching coordinates; one C-O bond length increases while the other decreases. Q = q1 - q2
When two or more normal coordinates belong to the same irreducible representation of the molecular point group (colloquially, have the same symmetry) there is "mixing" and the coefficients of the combination cannot be determined a priori. For example, in the linear molecule hydrogen cyanide, HCN, The two stretching vibrations are
- principally C-H stretching with a little C-N stretching; Q1 = q1 + a q2 (a << 1)
- principally C-N stretching with a little C-H stretching; Q2 = b q1 + q2 (b << 1)
The coefficients a and b are found by performing a full normal coordinate analysis by means of the Wilson GF method
GF method
The GF method, sometimes referred to as FG method, is a classical mechanical method introduced by E. Bright Wilson to obtain certain internal coordinates fora vibrating semi-rigid molecule, the so-called normal coordinates Qk...
.
Newtonian mechanics
Perhaps surprisingly, molecular vibrations can be treated using Newtonian mechanics to calculate the correct vibration frequencies. The basic assumption is that each vibration can be treated as though it corresponds to a spring. In the harmonic approximation the spring obeys Hooke's lawHooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
: the force required to extend the spring is proportional to the extension. The proportionality constant is known as a force constant, k. The anharmonic oscillator is considered elsewhere.
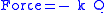
By Newton’s second law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
this force is also equal to a reduced mass
Reduced mass
Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
, μ, times acceleration.
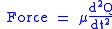
Since this is one and the same force the ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
follows.

The solution to this equation of simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
is

A is the maximum amplitude of the vibration coordinate Q. It remains to define the reduced mass, μ. In general, the reduced mass of a diatomic molecule, AB, is expressed in terms of the atomic masses, mA and mB, as
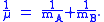
The use of the reduced mass ensures that the centre of mass of the molecule is not affected by the vibration. In the harmonic approximation the potential energy of the molecule is a quadratic function of the normal coordinate. It follows that the force-constant is equal to the second derivative of the potential energy.
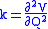
When two or more normal vibrations have the same symmetry a full normal coordinate analysis must be performed (see GF method
GF method
The GF method, sometimes referred to as FG method, is a classical mechanical method introduced by E. Bright Wilson to obtain certain internal coordinates fora vibrating semi-rigid molecule, the so-called normal coordinates Qk...
). The vibration frequencies,νi are obtained from the eigenvalues,λi, of the matrix product GF. G is a matrix of numbers derived from the masses of the atoms and the geometry of the molecule. F is a matrix derived from force-constant values. Details concerning the determination of the eigenvalues can be found in.
Quantum mechanics
In the harmonic approximation the potential energy is a quadratic function of the normal coordinates. Solving the Schrödinger wave equation, the energy states for each normal coordinate are given by ,
,where n is a quantum number that can take values of 0, 1, 2 ... The difference in energy when n changes by 1 are therefore equal to the energy derived using classical mechanics. See quantum harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
for graphs of the first 5 wave functions.
Knowing the wave functions, certain selection rules can be formulated. For example, for a harmonic oscillator transitions are allowed only when the quantum number n changes by one,
but this does not apply to an anharmonic oscillator; the observation of overtones is only possible because vibrations are anharmonic. Another consequence of anharmonicity is that transitions such as between states n=2 and n=1 have slightly less energy than transitions between the ground state and first excited state. Such a transition gives rise to a hot band
Hot transition
In molecular vibrational spectroscopy, a hot band is a transition between two states of a single normal mode of vibration, neither of which is the overall ground state. In infrared or Raman spectroscopy, hot bands refer to those transitions for a particular vibrational mode which arise from a...
.
Intensities
In an infrared spectrum the intensityIntensity (physics)
In physics, intensity is a measure of the energy flux, averaged over the period of the wave. The word "intensity" here is not synonymous with "strength", "amplitude", or "level", as it sometimes is in colloquial speech...
of an absorption band is proportional to the derivative of the molecular dipole moment with respect to the normal coordinate. The intensity of Raman bands depends on polarizability
Polarizability
Polarizability is the measure of the change in a molecule's electron distribution in response to an applied electric field, which can also be induced by electric interactions with solvents or ionic reagents. It is a property of matter...
.
See also
- Near infrared spectroscopyNear infrared spectroscopyNear-infrared spectroscopy is a spectroscopic method that uses the near-infrared region of the electromagnetic spectrum...
- Resonance Raman spectroscopyResonance Raman spectroscopyResonance Raman spectroscopy is a specialized implementation of the more general Raman spectroscopy.- Overview :As in Raman spectroscopy, RR spectroscopy provides information about the vibrations of molecules, and can also be used for identifying unknown substances. RR spectroscopy has found wide...
- Coherent anti-Stokes Raman spectroscopyCoherent anti-Stokes Raman spectroscopyCoherent anti-Stokes Raman spectroscopy, also called Coherent anti-Stokes Raman scattering spectroscopy , is a form of spectroscopy used primarily in chemistry, physics and related fields. It is sensitive to the same vibrational signatures of molecules as seen in Raman spectroscopy, typically the...
- Eckart conditionsEckart conditionsThe Eckart conditions, named after Carl Eckart, sometimes referred to as Sayvetz conditions, simplify the nuclear motion Schrödinger equation that arises in the second step of the Born-Oppenheimer approximation. The Eckart conditions allow to a large extent the separation of the external ...
- FG method
- Fermi resonanceFermi resonanceA Fermi resonance is the shifting of the energies and intensities of absorption bands in an infrared or Raman spectrum. It is a consequence of quantum mechanical mixing...
- Lennard-Jones potentialLennard-Jones potentialThe Lennard-Jones potential is a mathematically simple model that approximates the interaction between a pair of neutral atoms or molecules. A form of the potential was first proposed in 1924 by John Lennard-Jones...
- Transition dipole moment
Further reading
- P.M.A. Sherwood, Vibrational spectroscopy of solids, Cambridge University Press, 1972

