Atle Selberg
Encyclopedia
Atle Selberg was a Norwegian
mathematician
known for his work in analytic number theory
, and in the theory of automorphic form
s, in particular bringing them into relation with spectral theory
. He was awarded the Fields Medal
in 1950.
, Norway
.
While he was still at school he was influenced by the work of Srinivasa Ramanujan
and he discovered the exact analytical formula for the partition function as suggested by the works of Ramanujan, however, this result was first published by Hans Rademacher
. During the war he fought against the German invasion of Norway, and was imprisoned several times.
He studied at the University of Oslo
and completed his Ph.D.
in 1943.
, Selberg worked in isolation due to the German occupation of Norway. After the war his accomplishments became known, including a proof that a positive proportion of the zeros of the Riemann zeta function lie on the line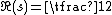
.
After the war, he turned to sieve theory
, a previously neglected topic which Selberg's work brought into prominence. In a 1947 paper he introduced the Selberg sieve
, a method well adapted in particular to providing auxiliary upper bounds, and which contributed to Chen's theorem
, among other important results.
In March 1948, Selberg established, by elementary means, the asymptotic formula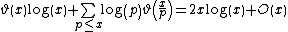
where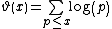
for primes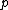
. By July of that year, Selberg and Paul Erdős
had each obtained elementary proof
s of the prime number theorem
, both using Selberg's then unpublished asymptotic formula as a starting point. Circumstances leading up to the proofs, as well as publication disagreements, led to a bitter dispute between the two mathematicians.
For his fundamental accomplishments during the 1940s, Selberg received the 1950 Fields Medal
.
and settled at the Institute for Advanced Study
in Princeton, New Jersey
in the 1950s where he remained until his death. During the 1950s he worked on introducing spectral theory
into number theory
, culminating in his development of the Selberg trace formula
, the most famous and influential of his results. In its simplest form, this establishes a duality between the lengths of closed geodesic
s on a compact Riemann surface
and the eigenvalues of the Laplacian
, which is analogous to the duality between the prime number
s and the zeros of the zeta function. He was awarded the 1986 Wolf Prize in Mathematics
.
Selberg received many distinctions for his work in addition to the Fields Medal
, the Wolf Prize and the Gunnerus Medal
. He was elected to the Norwegian Academy of Science and Letters
, the Royal Danish Academy of Sciences and Letters
and the American Academy of Arts and Sciences
.
Selberg had two children, Ingrid Selberg and Lars Selberg. Ingrid Selberg is married to playwright Mustapha Matura
.
He died at home in Princeton on 6 August 2007 of heart failure.
Norway
Norway , officially the Kingdom of Norway, is a Nordic unitary constitutional monarchy whose territory comprises the western portion of the Scandinavian Peninsula, Jan Mayen, and the Arctic archipelago of Svalbard and Bouvet Island. Norway has a total area of and a population of about 4.9 million...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
known for his work in analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
, and in the theory of automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s, in particular bringing them into relation with spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
. He was awarded the Fields Medal
Fields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
in 1950.
Early years
Selberg was born in LangesundLangesund
is the administrative centre of the municipality of Bamble, Norway.The town of Langesund was established as a municipality January 1, 1838...
, Norway
Norway
Norway , officially the Kingdom of Norway, is a Nordic unitary constitutional monarchy whose territory comprises the western portion of the Scandinavian Peninsula, Jan Mayen, and the Arctic archipelago of Svalbard and Bouvet Island. Norway has a total area of and a population of about 4.9 million...
.
While he was still at school he was influenced by the work of Srinivasa Ramanujan
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
and he discovered the exact analytical formula for the partition function as suggested by the works of Ramanujan, however, this result was first published by Hans Rademacher
Hans Rademacher
Hans Adolph Rademacher was a German mathematician, known for work in mathematical analysis and number theory.-Biography:...
. During the war he fought against the German invasion of Norway, and was imprisoned several times.
He studied at the University of Oslo
University of Oslo
The University of Oslo , formerly The Royal Frederick University , is the oldest and largest university in Norway, situated in the Norwegian capital of Oslo. The university was founded in 1811 and was modelled after the recently established University of Berlin...
and completed his Ph.D.
Ph.D.
A Ph.D. is a Doctor of Philosophy, an academic degree.Ph.D. may also refer to:* Ph.D. , a 1980s British group*Piled Higher and Deeper, a web comic strip*PhD: Phantasy Degree, a Korean comic series* PhD Docbook renderer, an XML renderer...
in 1943.
World War II
During World War IIWorld War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
, Selberg worked in isolation due to the German occupation of Norway. After the war his accomplishments became known, including a proof that a positive proportion of the zeros of the Riemann zeta function lie on the line
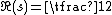.After the war, he turned to sieve theory
Sieve theory
Sieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The primordial example of a sifted set is the set of prime numbers up to some prescribed limit X. Correspondingly, the primordial example of a...
, a previously neglected topic which Selberg's work brought into prominence. In a 1947 paper he introduced the Selberg sieve
Selberg sieve
In mathematics, in the field of number theory, the Selberg sieve is a technique for estimating the size of "sifted sets" of positive integers which satisfy a set of conditions which are expressed by congruences...
, a method well adapted in particular to providing auxiliary upper bounds, and which contributed to Chen's theorem
Chen's theorem
right|thumb|Chen JingrunChen's theorem states that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime . The theorem was first stated by Chinese mathematician Chen Jingrun in 1966, with further details of the proof in 1973. His original...
, among other important results.
In March 1948, Selberg established, by elementary means, the asymptotic formula
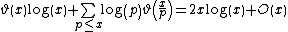
where
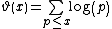
for primes
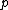. By July of that year, Selberg and Paul ErdősPaul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
had each obtained elementary proof
Elementary proof
In mathematics, an elementary proof is a mathematical proof that only uses basic techniques. More specifically, the term is used in number theory to refer to proofs that make no use of complex analysis. For some time it was thought that certain theorems, like the prime number theorem, could only be...
s of the prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
, both using Selberg's then unpublished asymptotic formula as a starting point. Circumstances leading up to the proofs, as well as publication disagreements, led to a bitter dispute between the two mathematicians.
For his fundamental accomplishments during the 1940s, Selberg received the 1950 Fields Medal
Fields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
.
Institute for Advanced Study
Selberg moved to the United StatesUnited States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
and settled at the Institute for Advanced Study
Institute for Advanced Study
The Institute for Advanced Study, located in Princeton, New Jersey, United States, is an independent postgraduate center for theoretical research and intellectual inquiry. It was founded in 1930 by Abraham Flexner...
in Princeton, New Jersey
Princeton, New Jersey
Princeton is a community located in Mercer County, New Jersey, United States. It is best known as the location of Princeton University, which has been sited in the community since 1756...
in the 1950s where he remained until his death. During the 1950s he worked on introducing spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
into number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, culminating in his development of the Selberg trace formula
Selberg trace formula
In mathematics, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation of G on the space L2 of square-integrable functions, where G is a Lie group and Γ a cofinite discrete group...
, the most famous and influential of his results. In its simplest form, this establishes a duality between the lengths of closed geodesic
Closed geodesic
In differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold M is the projection of a closed orbit of the geodesic flow on M.-Examples:On the unit sphere, every great circle is an example of a closed geodesic...
s on a compact Riemann surface
Compact Riemann surface
In mathematics, a compact Riemann surface is a complex manifold of dimension one that is a compact space. Riemann surfaces are generally classified first into the compact and the open .A compact Riemann surface C that is a...
and the eigenvalues of the Laplacian
Laplace-Beltrami operator
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
, which is analogous to the duality between the prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s and the zeros of the zeta function. He was awarded the 1986 Wolf Prize in Mathematics
Wolf Prize in Mathematics
The Wolf Prize in Mathematics is awarded almost annually by the Wolf Foundation in Israel. It is one of the six Wolf Prizes established by the Foundation and awarded since 1978; the others are in Agriculture, Chemistry, Medicine, Physics and Arts...
.
Selberg received many distinctions for his work in addition to the Fields Medal
Fields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
, the Wolf Prize and the Gunnerus Medal
Gunnerus Medal
The Gunnerus Medal is a medal awarded by the learned society Royal Norwegian Society of Sciences and Letters.It was inaugurated in 1927, and named after Johan Ernst Gunnerus, founder of the learned society...
. He was elected to the Norwegian Academy of Science and Letters
Norwegian Academy of Science and Letters
The Norwegian Academy of Science and Letters is a learned society based in Oslo, Norway.-History:The University of Oslo was established in 1811. The idea of a learned society in Christiania surfaced for the first time in 1841. The city of Throndhjem had no university, but had a learned...
, the Royal Danish Academy of Sciences and Letters
Royal Danish Academy of Sciences and Letters
Royal Danish Academy of Sciences and Letters is a Danish non-governmental science Academy, founded 13 November 1742 by permission of the King Christian VI, as a historical Collegium Antiquitatum...
and the American Academy of Arts and Sciences
American Academy of Arts and Sciences
The American Academy of Arts and Sciences is an independent policy research center that conducts multidisciplinary studies of complex and emerging problems. The Academy’s elected members are leaders in the academic disciplines, the arts, business, and public affairs.James Bowdoin, John Adams, and...
.
Selberg had two children, Ingrid Selberg and Lars Selberg. Ingrid Selberg is married to playwright Mustapha Matura
Mustapha Matura
Mustapha Matura is a Trinidadian playwright living in London.In 1971 his play As Time Goes By was first performed at the Traverse Theatre Club in Edinburgh and the Theatre Upstairs at the Royal Court Theatre, with a cast of noted Caribbean actors including Stefan Kalipha, Alfred Fagon, Mona...
.
He died at home in Princeton on 6 August 2007 of heart failure.
Selected publications
- Atle Selberg Collected Papers: 1 (Springer-Verlag, Heidelberg), ISBN 0-387-18389-2
- Collected Papers (Springer-Verlag, Heidelberg Mai 1998), ISBN 3-540-50626-8
See also
- Chowla–Selberg formula
- Critical line theorem
- Maass–Selberg relationsMaass–Selberg relationsIn mathematics, the Maass–Selberg relations are some relations describing the inner products of truncated real analytic Eisenstein series, that in some sense say that distinct Eisenstein series are orthogonal. introduced the Maass–Selberg relations for the case of real analytic Eisenstein series...
- Selberg classSelberg classIn mathematics, the Selberg class S is an axiomatic definition of a class of L-functions. The members of the class are Dirichlet series which obey four axioms that seem to capture the essential properties satisfied by most functions that are commonly called L-functions or zeta functions...
- Selberg's conjectureSelberg's conjectureIn mathematics, the Selberg conjecture, named after Atle Selberg, is about the density of zeros of the Riemann zeta function \zeta\bigl. It is known that the function has infinitely many zeroes on this line in the complex plane: the point at issue is how densely they are clustered...
- Selberg integral
- Selberg trace formulaSelberg trace formulaIn mathematics, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation of G on the space L2 of square-integrable functions, where G is a Lie group and Γ a cofinite discrete group...
- Selberg zeta function