Second moment of area
Encyclopedia
The second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending
and deflection
, around an axis that lies in the cross-sectional plane. The deflection of a beam under load depends not only on the load, but also on the geometry of the beam's cross-section. This is why beams with higher area moments of inertia, such as -beams
(properly denoted as: wide-flange beams), are so often seen in building construction as opposed to other beams with the same cross sectional area.
The second moment of area differs from polar moment of inertia of area
in the direction of the axis of bending
or torsion
relative to the plane of the cross-section; in the latter, the axis is perpendicular to this plane. The third kind of moment of inertia not to be confused with involves angular kinetic energy or momentum
. Often, each of these may simply be referred to as "moment of inertia," and the same symbols, I or J, may be used, sometimes with a qualifying subscript. Which inertia is meant (bending, twisting, or kinetic) is usually clear from the context, if not from the unit
s: both moments of area have units of length to the fourth power [m4] (distinguished only by whether a beam is being bent or torqued), whereas the kinetic moment of inertia of mass
has units of mass times length squared [kg*m2].
-beam
with a weight on the end. If the beam is long, we assume the dominant deflection mode will be bending
rather than shear
. Thinking of the beam as made of elements along its length, like sliced bread, consider the load on one of these slices. The load will be a bending moment
. Let the beam lie along the x axis with z pointing up. The bending moment would be around the y axis. The top will be in tension; the bottom will be in compression, and a horizontal line middle parallel with the y axis will experience no load. We wish to describe the effects on beam stiffness due to the cross-sectional shape of the beam as a single number (or, in the case that we want to consider more than one loading direction, as a symmetric tensor
, which we can represent as a 2×2 matrix); this will be the second moment of area.
Assuming linear elasticity
, the restoring stress that any point in the beam will provide, is proportional to the strain
it experiences. This stress-strain relationship can be described by Hooke's law
. The energy will be proportional to the square of the strain. Geometrically, the strain in the beam will be maximum at the top, decrease linearly to zero at the medial axis, and continue to decrease linearly to the bottom. Thus, the energy stored in a cross-sectional slice of the beam bent by some amount will be proportional to the sum of the square of the distance to the medial axis. In particular, the actual energy storage will also be proportional to the length of the beam and the stiffness of the material. This strain-energy storage is described well by the Minimum total potential energy principle
.
Considering only the factor due to the cross-sectional shape of the beam gives the second moment of area:
where
When the line λ is the x axis and the bending force is parallel to the z axis, the second moment of area can be computed as
For calculating the stresses of bending, the above can only be used on its own when sections are symmetrical about the x-axis. When this is not the case, the second moment of area about both the x- and the y-axis and the product moment of area, Ixy (see below), are required.
running along the x axis but oriented so that its surface normal
is in the (0,1,1) direction. If you push down on it (0,0,−1), that will result in a bending moment
in the (0,1,0) direction. However, although it will move down, it will primarily deflect in the (0,−1,−1) direction. This behavior is captured by the product moment of area. The product moment of area, Ixy is defined as
A coordinate system in which the product moment is zero is referred to as a set of principal axes, and the second moments of area calculated with respect to the principal axes will assume their maxima and minima
. This is a direct result of the spectral theorem
applied to the moment tensor, described below; because it is symmetric positive semi-definite.
—an object that provides deflection direction and magnitude, or elastic energy, as a function of loading direction.
Much like the mass moment of inertia
, the area moment of inertia tensor is
where is the Kronecker delta.
is the Kronecker delta.
The reason for the as opposed to just the outer product
as opposed to just the outer product
, , is that the tensor operates on moments. That is, we would like the expression
, is that the tensor operates on moments. That is, we would like the expression
to be proportional to the energy for a given torque
, . See Moment of inertia#Comparison with covariance matrix for details.
. See Moment of inertia#Comparison with covariance matrix for details.
The product moment of area is significant for determining the bending stress
in an asymmetric cross section. Unlike the second moments of area, the product moment may give both negative and positive values.
to the fourth power (typically mm4, in4, etc.)
of vectors, this tensor transforms as a type (0,2) tensor.
can be used to determine the moment of an object about any axis, given the moment of inertia (second moment of area) of the object about the parallel axis through the object's center of mass (or centroid
) and the perpendicular distance between the axes.



The value of the angle , which will give a product moment of zero, is equal to:
, which will give a product moment of zero, is equal to:

This angle is the angle between the axes of the original coordinate system and the principal axes of the cross section.
for a beam
in co-ordinate system having origin located at the neutral axis
of the beam is (Pilkey 2002, p. 17):

If the coordinate system is chosen to give a product moment of area equal to zero, the formula simplifies to:

If additionally the beam is only subjected to bending about one axis, the formula simplifies further:




This equation is useful in calculating the required strength of masts in compression. Taking the area moment of inertia calculated from the previous formula, and entering it into Euler's formula gives the maximum force that a mast can theoretically withstand before buckling.


 The -beam can be analyzed as either three pieces added together or as a large piece with two pieces removed from it. Either of these methods will require use of the formula for composite cross section. This section only covers doubly symmetric -beams, meaning the shape has two planes of symmetry.
The -beam can be analyzed as either three pieces added together or as a large piece with two pieces removed from it. Either of these methods will require use of the formula for composite cross section. This section only covers doubly symmetric -beams, meaning the shape has two planes of symmetry.
This formula uses the method of a block with two pieces removed. (While this may not be the easiest way to do this calculation, it is instructive in demonstrating how to subtract moments).
 Since the -beam is symmetrical with respect to the y-axis the
Since the -beam is symmetrical with respect to the y-axis the  has no component for the centroid
has no component for the centroid
of the blocks removed being offset above or below the x axis.

When computing Iy it is necessary to allow for the fact that the pieces being removed are offset from the Y axis, this results in the Ax2 term.

Doing the same calculation by combining three pieces, the center webbing plus identical contributions for the top and bottom piece:
Since the centroids of all three pieces are on the y-axis Iy can be computed just by adding the moments together.

However, this time the law for composition with offsets must be used for Ix because the centroids of the top and bottom are offset from the centroid of the whole -beam.

on XY plane can be computed in a generic way by summing contributions from each segment of a polygon.
For each segment defined by two consecutive points of the polygon, consider a triangle with two corners at these points and third corner at the origin of the coordinates. Integration by the area of that triangle and summing by the polygon segments yields:



These formulae imply that points defining the polygon are ordered in anticlockwise manner; for clockwisely defined polygons it will give negative values. See polygon area for calculating area
and centroid
of the section using similar formulae.
Bending
In engineering mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically...
and deflection
Deflection (engineering)
In engineering, deflection is the degree to which a structural element is displaced under a load. It may refer to an angle or a distance.The deflection distance of a member under a load is directly related to the slope of the deflected shape of the member under that load and can be calculated by...
, around an axis that lies in the cross-sectional plane. The deflection of a beam under load depends not only on the load, but also on the geometry of the beam's cross-section. This is why beams with higher area moments of inertia, such as -beams
I-beam
-beams, also known as H-beams, W-beams , rolled steel joist , or double-T are beams with an - or H-shaped cross-section. The horizontal elements of the "" are flanges, while the vertical element is the web...
(properly denoted as: wide-flange beams), are so often seen in building construction as opposed to other beams with the same cross sectional area.
The second moment of area differs from polar moment of inertia of area
Polar moment of inertia
Polar moment of inertia is a quantity used to predict an object's ability to resist torsion, in objects with an invariant circular cross section and no significant warping or out-of-plane deformation. It is used to calculate the angular displacement of an object subjected to a torque...
in the direction of the axis of bending
Bending
In engineering mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically...
or torsion
Torsion (mechanics)
In solid mechanics, torsion is the twisting of an object due to an applied torque. In sections perpendicular to the torque axis, the resultant shear stress in this section is perpendicular to the radius....
relative to the plane of the cross-section; in the latter, the axis is perpendicular to this plane. The third kind of moment of inertia not to be confused with involves angular kinetic energy or momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
. Often, each of these may simply be referred to as "moment of inertia," and the same symbols, I or J, may be used, sometimes with a qualifying subscript. Which inertia is meant (bending, twisting, or kinetic) is usually clear from the context, if not from the unit
Units of measurement
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
s: both moments of area have units of length to the fourth power [m4] (distinguished only by whether a beam is being bent or torqued), whereas the kinetic moment of inertia of mass
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
has units of mass times length squared [kg*m2].
Intuition
Consider the problem of determining the deflection of a beam of uniform material and uniform cross section. In particular, suppose we have a cantileveredCantilever
A cantilever is a beam anchored at only one end. The beam carries the load to the support where it is resisted by moment and shear stress. Cantilever construction allows for overhanging structures without external bracing. Cantilevers can also be constructed with trusses or slabs.This is in...
-beam
I-beam
-beams, also known as H-beams, W-beams , rolled steel joist , or double-T are beams with an - or H-shaped cross-section. The horizontal elements of the "" are flanges, while the vertical element is the web...
with a weight on the end. If the beam is long, we assume the dominant deflection mode will be bending
Bending
In engineering mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically...
rather than shear
Shearing (physics)
Shearing in continuum mechanics refers to the occurrence of a shear strain, which is a deformation of a material substance in which parallel internal surfaces slide past one another. It is induced by a shear stress in the material...
. Thinking of the beam as made of elements along its length, like sliced bread, consider the load on one of these slices. The load will be a bending moment
Bending Moment
A bending moment exists in a structural element when a moment is applied to the element so that the element bends. Moments and torques are measured as a force multiplied by a distance so they have as unit newton-metres , or pound-foot or foot-pound...
. Let the beam lie along the x axis with z pointing up. The bending moment would be around the y axis. The top will be in tension; the bottom will be in compression, and a horizontal line middle parallel with the y axis will experience no load. We wish to describe the effects on beam stiffness due to the cross-sectional shape of the beam as a single number (or, in the case that we want to consider more than one loading direction, as a symmetric tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, which we can represent as a 2×2 matrix); this will be the second moment of area.
Assuming linear elasticity
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
, the restoring stress that any point in the beam will provide, is proportional to the strain
Deformation (mechanics)
Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body...
it experiences. This stress-strain relationship can be described by Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
. The energy will be proportional to the square of the strain. Geometrically, the strain in the beam will be maximum at the top, decrease linearly to zero at the medial axis, and continue to decrease linearly to the bottom. Thus, the energy stored in a cross-sectional slice of the beam bent by some amount will be proportional to the sum of the square of the distance to the medial axis. In particular, the actual energy storage will also be proportional to the length of the beam and the stiffness of the material. This strain-energy storage is described well by the Minimum total potential energy principle
Minimum total potential energy principle
The principle of minimum total potential energy is a fundamental concept used in physics, chemistry, biology, and engineering. It asserts that a structure or body shall deform or displace to a position that minimizes the total potential energy, with the lost potential energy being dissipated as heat...
.
Considering only the factor due to the cross-sectional shape of the beam gives the second moment of area:

Definition
Let A be a beam cross section perpendicular to the beam's axis. That is, A is a plane region of a particular shape. Let λ be a straight line in the plane (by definition, perpendicular to the axis of the beam). Then the second moment of area of the region A about the line λ iswhere
- Iλ = the second moment of area about the line λ
- dA = an elemental area
- n = the perpendicular distance from the line λ to the element dA
When the line λ is the x axis and the bending force is parallel to the z axis, the second moment of area can be computed as
For calculating the stresses of bending, the above can only be used on its own when sections are symmetrical about the x-axis. When this is not the case, the second moment of area about both the x- and the y-axis and the product moment of area, Ixy (see below), are required.
Product moment of area
While the scalar second moment of area about an axis describes a beam's resistance to bending along that axis, some beams will deflect in a direction other than the direction they are loaded. For example, imagine a leaf springLeaf spring
Originally called laminated or carriage spring, a leaf spring is a simple form of spring, commonly used for the suspension in wheeled vehicles...
running along the x axis but oriented so that its surface normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
is in the (0,1,1) direction. If you push down on it (0,0,−1), that will result in a bending moment
Bending Moment
A bending moment exists in a structural element when a moment is applied to the element so that the element bends. Moments and torques are measured as a force multiplied by a distance so they have as unit newton-metres , or pound-foot or foot-pound...
in the (0,1,0) direction. However, although it will move down, it will primarily deflect in the (0,−1,−1) direction. This behavior is captured by the product moment of area. The product moment of area, Ixy is defined as
- dA = an elemental area
- x = the perpendicular distance to the element dA from the axis y
- y = the perpendicular distance to the element dA from the axis x
- Note that Ixy is defined here with positive sign following common practice adopted in structural analysis (see e.g., Pilkey 2002, p. 15).
A coordinate system in which the product moment is zero is referred to as a set of principal axes, and the second moments of area calculated with respect to the principal axes will assume their maxima and minima
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
. This is a direct result of the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
applied to the moment tensor, described below; because it is symmetric positive semi-definite.
Second moment of area tensor
Keeping track of both second moment of area and product moment of area is confusing and tedious. A holistic approach is to note that a second moment of area is fundamentally a tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
—an object that provides deflection direction and magnitude, or elastic energy, as a function of loading direction.
Much like the mass moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
, the area moment of inertia tensor is

where
 is the Kronecker delta.
is the Kronecker delta.The reason for the
 as opposed to just the outer product
as opposed to just the outer productOuter product
In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
,
 , is that the tensor operates on moments. That is, we would like the expression
, is that the tensor operates on moments. That is, we would like the expression
to be proportional to the energy for a given torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
,
 . See Moment of inertia#Comparison with covariance matrix for details.
. See Moment of inertia#Comparison with covariance matrix for details.The product moment of area is significant for determining the bending stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
in an asymmetric cross section. Unlike the second moments of area, the product moment may give both negative and positive values.
Unit
The unit for second moment of area is lengthLength
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
to the fourth power (typically mm4, in4, etc.)
Co-ordinate transformations
When calculating moments of the section it is often practical to compute them in one co-ordinate system (typically bound to the section shape) and then transform to another one using co-ordinate transformations. As an outer productOuter product
In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
of vectors, this tensor transforms as a type (0,2) tensor.
Parallel axis theorem
The parallel axis theoremParallel axis theorem
In physics, the parallel axis theorem or Huygens-Steiner theorem can be used to determine the second moment of area or the mass moment of inertia of a rigid body about any axis, given the body's moment of inertia about a parallel axis through the object's centre of mass and the perpendicular...
can be used to determine the moment of an object about any axis, given the moment of inertia (second moment of area) of the object about the parallel axis through the object's center of mass (or centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
) and the perpendicular distance between the axes.
-

- Ix = the second moment of area with respect to the x-axis
- IxCG = the second moment of area with respect to an axis parallel to x and passing through the centroid of the shape (coincides with the neutral axisNeutral axisThe neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid...
) - A = area of the shape
- d = the distance between the x-axis and the centroidal axis
Axis rotation
The following formulae can be used to calculate moments of the section in a co-ordinate system rotated relative to the original co-ordinate system:


 = the angle of rotation (anticlockwise sense):
= the angle of rotation (anticlockwise sense):

- Ix, Iy and Ixy = the second moments and the product moment of area in the original coordinate system
- Ix*, Iy* and Ixy* = the second moments and the product moment of area in the rotated coordinate system.
The value of the angle
 , which will give a product moment of zero, is equal to:
, which will give a product moment of zero, is equal to:
This angle is the angle between the axes of the original coordinate system and the principal axes of the cross section.
Stress in a beam
The general form of the classic bending formulaEuler-Bernoulli beam equation
Euler–Bernoulli beam theory is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case for small deflections of a beam which is subjected to lateral loads only...
for a beam
Beam (structure)
A beam is a horizontal structural element that is capable of withstanding load primarily by resisting bending. The bending force induced into the material of the beam as a result of the external loads, own weight, span and external reactions to these loads is called a bending moment.- Overview...
in co-ordinate system having origin located at the neutral axis
Neutral axis
The neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid...
of the beam is (Pilkey 2002, p. 17):

 is the normal stressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is the normal stressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
in the beam due to bending- x = the perpendicular distance to the centroidal y-axis
- y = the perpendicular distance to the centroidal x-axis
- My = the bending moment about the y-axis
- Mx = the bending moment about the x-axis
- Ix = the second moment of area about x-axis
- Iy = the second moment of area about y-axis
- Ixy = the product moment of area
If the coordinate system is chosen to give a product moment of area equal to zero, the formula simplifies to:

If additionally the beam is only subjected to bending about one axis, the formula simplifies further:

Second moment of area for various cross sections
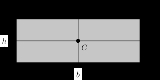
See list of area moments of inertia for other cross sections.Rectangular cross section



- b = width (x-dimension),
- h = height (y-dimension)
Circular cross section

- r = radius
This equation is useful in calculating the required strength of masts in compression. Taking the area moment of inertia calculated from the previous formula, and entering it into Euler's formula gives the maximum force that a mast can theoretically withstand before buckling.

 is the Young's (elastic) modulus of materialYoung's modulusYoung's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
is the Young's (elastic) modulus of materialYoung's modulusYoung's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain... is the second moment of area of the mast
is the second moment of area of the mast is the pinned length of the mast
is the pinned length of the mast
Hollow Cylindrical Cross Section

 = outside diameter
= outside diameter = inside diameter
= inside diameter = outside radius
= outside radius = inside radius
= inside radius
Composite cross section
When it is easier to compute the moment for an item as a combination of pieces, the second moment of area is calculated by applying the parallel axis theorem to each piece and adding the terms:- y = distance from x-axis
- x = distance from y-axis
- A = surface area of part
- Ilocal is the second moment of area for that part of the composite, in the appropriate direction (i.e. Ix or Iy respectively).
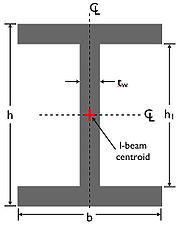
"-beam" cross section

- b = width (x-dimension),
- h = height (y-dimension)
- tw = width of central webbing
- h1 = inside distance between flanges (usually referred to as hw, the height of the web)
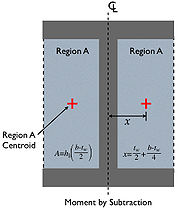
This formula uses the method of a block with two pieces removed. (While this may not be the easiest way to do this calculation, it is instructive in demonstrating how to subtract moments).

 has no component for the centroid
has no component for the centroidCentroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
of the blocks removed being offset above or below the x axis.

When computing Iy it is necessary to allow for the fact that the pieces being removed are offset from the Y axis, this results in the Ax2 term.

- A = Area contained within the middle of one of the 'C' shapes of created by two flanges and the webbing on one side of the cross section =

- x = distance of the centroid of the area contained in the 'C' shape from the y-axis of the beam =

Doing the same calculation by combining three pieces, the center webbing plus identical contributions for the top and bottom piece:
Since the centroids of all three pieces are on the y-axis Iy can be computed just by adding the moments together.

However, this time the law for composition with offsets must be used for Ix because the centroids of the top and bottom are offset from the centroid of the whole -beam.
- A = Area of the top or bottom piece =

- y = offset of the centroid of the top or bottom piece from the centroid of the whole -beam =


Any cross section defined as polygon
The second moments of area for any cross section defined as a simple polygonSimple polygon
In geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
on XY plane can be computed in a generic way by summing contributions from each segment of a polygon.
For each segment defined by two consecutive points of the polygon, consider a triangle with two corners at these points and third corner at the origin of the coordinates. Integration by the area of that triangle and summing by the polygon segments yields:



-
 is twice the (signed) area of the elementary triangle,
is twice the (signed) area of the elementary triangle, - index i passes over all n points in the polygon, which is considered closed, i.e. point n is point 1
These formulae imply that points defining the polygon are ordered in anticlockwise manner; for clockwisely defined polygons it will give negative values. See polygon area for calculating area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
and centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
of the section using similar formulae.
See also
- List of area moments of inertia
- List of moments of inertia
- Moment of inertiaMoment of inertiaIn classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
- Polar moment of inertiaPolar moment of inertiaPolar moment of inertia is a quantity used to predict an object's ability to resist torsion, in objects with an invariant circular cross section and no significant warping or out-of-plane deformation. It is used to calculate the angular displacement of an object subjected to a torque...
- Parallel axis theoremParallel axis theoremIn physics, the parallel axis theorem or Huygens-Steiner theorem can be used to determine the second moment of area or the mass moment of inertia of a rigid body about any axis, given the body's moment of inertia about a parallel axis through the object's centre of mass and the perpendicular...
- Perpendicular axis theoremPerpendicular axis theoremIn physics, the perpendicular axis theorem can be used to determine the moment of inertia of a rigid object that lies entirely within a plane, about an axis perpendicular to the plane, given the moments of inertia of the object about two perpendicular axes lying within the plane...






