The following is list of area moments of inertia

Second moment of area

The second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane...

. The area moment of inertia or second moment of area has a unit of dimension length⁴, and should not be confused with the mass moment of inertia. If the piece is thin, however, the mass moment of inertia equals the areal density times the area moment of inertia. Each is with respect to a horizontal axis through the centroid

Centroid

In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...

 of the given shape, unless otherwise specified.

Description	Figure	Area moment of inertia	Comment	Reference
a filled circular area of radius r
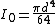an annulus Annulus (mathematics) In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...  of inner radiusr1 and outer radiusr2		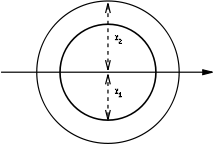	For thin tubes, this is approximately equal to: or .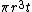
a filled circular sector Circular sector A circular sector or circle sector, is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle in radians, r the radius of the circle, and L is the arc length of the...  of angle θ in radian Radian Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit... s and radius r with respect to an axis through the centroid of the sector and the centre of the circle
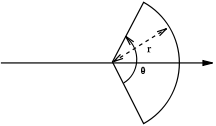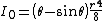a filled semicircle with radius r with respect to a horizontal line passing through the centroid of the area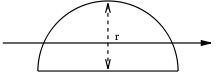
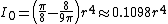a filled semicircle as above but with respect to an axis collinear with the base		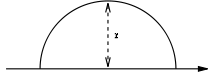	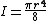This is a consequence of the parallel axis theorem Parallel axis theorem In physics, the parallel axis theorem or Huygens-Steiner theorem can be used to determine the second moment of area or the mass moment of inertia of a rigid body about any axis, given the body's moment of inertia about a parallel axis through the object's centre of mass and the perpendicular...  and the fact that the distance between these two axes is
a filled semicircle as above but with respect to a vertical axis through the centroid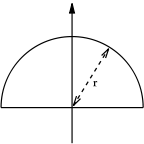
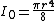a filled quarter circle with radius r entirely in the 1st quadrant of the Cartesian coordinate system Cartesian coordinate system A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
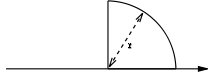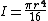a filled quarter circle as above but with respect to a horizontal or vertical axis through the centroid		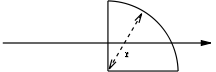	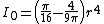This is a consequence of the parallel axis theorem Parallel axis theorem In physics, the parallel axis theorem or Huygens-Steiner theorem can be used to determine the second moment of area or the mass moment of inertia of a rigid body about any axis, given the body's moment of inertia about a parallel axis through the object's centre of mass and the perpendicular...  and the fact that the distance between these two axes is
a filled ellipse Ellipse In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...  whose radius along the x-axis is a and whose radius along the y-axis is b
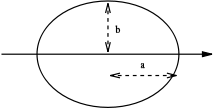a filled rectangular area with a base width of b and height h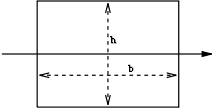
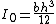a filled rectangular area as above but with respect to an axis collinear with the base		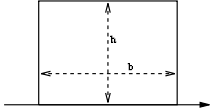	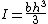This is a result from the parallel axis theorem Parallel axis theorem In physics, the parallel axis theorem or Huygens-Steiner theorem can be used to determine the second moment of area or the mass moment of inertia of a rigid body about any axis, given the body's moment of inertia about a parallel axis through the object's centre of mass and the perpendicular...
a filled rectangular area as above but with respect to an axis collinear, where r is the perpendicular distance from the centroid of the rectangle to the axis of interest		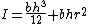	This is a result from the parallel axis theorem Parallel axis theorem In physics, the parallel axis theorem or Huygens-Steiner theorem can be used to determine the second moment of area or the mass moment of inertia of a rigid body about any axis, given the body's moment of inertia about a parallel axis through the object's centre of mass and the perpendicular...
a filled triangular area with a base width of b and height h with respect to an axis through the centroid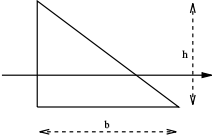
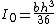a filled triangular area as above but with respect to an axis collinear with the base		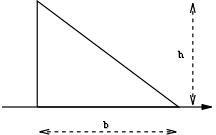	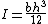This is a consequence of the parallel axis theorem Parallel axis theorem In physics, the parallel axis theorem or Huygens-Steiner theorem can be used to determine the second moment of area or the mass moment of inertia of a rigid body about any axis, given the body's moment of inertia about a parallel axis through the object's centre of mass and the perpendicular...
a filled regular hexagon with a side length of a		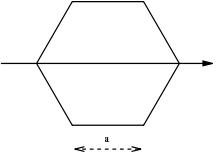	The result is valid for both a horizontal and a vertical axis through the centroid, and therefore is also valid for an axis with arbitrary direction that passes through the origin.