List of moments of inertia - AbsoluteAstronomy.com

The following is a list of moments of inertia

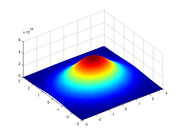
Moment of inertia

In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...

. Mass moments of inertia have units of dimension mass × length². It is the rotational analogue to mass. It should not be confused with the second moment of area

Second moment of area

The second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane...

(area moment of inertia), which is used in bending calculations.

The following moments of inertia assume constant density throughout the object, and the axis of rotation is taken to be through the center of mass, unless otherwise specified.

Description	Figure	Moment(s) of inertia	Comment
Point mass m at a distance r from the axis of rotation.			—
Two point masses, M and m, with reduced mass Reduced mass Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not... and separated by a distance, x.			—
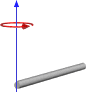
Rod Rod (geometry) In geometry, a rod is a three-dimensional, solid cylinder.... of length L and mass m (Axis of rotation at the end of the rod)			This expression assumes that the rod is an infinitely thin (but rigid) wire. This is also a special case of the thin rectangular plate with axis of rotation at the end of the plate, with h = L and w = 0.
Rod Rod (geometry) In geometry, a rod is a three-dimensional, solid cylinder.... of length L and mass m			This expression assumes that the rod is an infinitely thin (but rigid) wire. This is a special case of the thin rectangular plate with axis of rotation at the center of the plate, with w = L and h = 0.
Thin circular hoop Hoop Hoop may refer to:Hoop is one apparatus in Rhythmic GymnasticsHoop , an American basketball magazine"Hoops" , a song by RubyHoops , a basketball video game... of radius r and mass m			This is a special case of a torus Torus In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle... for b=0. (See below.), as well as of a thick-walled cylindrical tube with open ends, with r₁=r₂ and h=0.
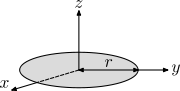
Thin, solid disk Disk (mathematics) In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary... of radius r and mass m			This is a special case of the solid cylinder, with h=0.
Thin cylindrical Cylinder (geometry) A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder... shell with open ends, of radius r and mass m			This expression assumes the shell thickness is negligible. It is a special case of the thick-walled cylindrical tube for r₁=r₂. Also, a point mass (m) at the end of a rod of length r has this same moment of inertia and the value r is called the radius of gyration Radius of gyration Radius of gyration or gyradius is the name of several related measures of the size of an object, a surface, or an ensemble of points. It is calculated as the root mean square distance of the objects' parts from either its center of gravity or an axis.... .
Solid cylinder of radius r, height h and mass m		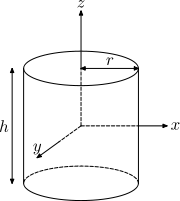	This is a special case of the thick-walled cylindrical tube, with r₁=0. (Note: X-Y axis should be swapped for a standard right handed frame)
Thick-walled cylindrical tube with open ends, of inner radius r₁, outer radius r₂, length h and mass m		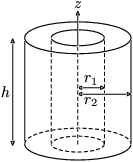or when defining the normalized thickness t_n = t/r and letting r = r₂, then	With a density of ρ and the same geometry
Sphere Sphere A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point... (hollow) of radius r and mass m			A hollow sphere can be taken to be made up of two stacks of infinitesimally thin, circular hoops, where the radius differs from 0 to r (or a single stack, , where the radius differs from -r to r).
Ball Ball (mathematics) In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball .... (solid) of radius r and mass m		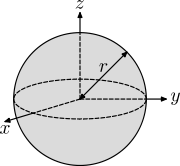	A sphere can be taken to be made up of two stacks of infinitesimally thin, solid discs, where the radius differs from 0 to r (or a single stack, where the radius differs from -r to r). Also, it can be taken to be made up of infinitesimally thin, hollow spheres, where the radius differs from 0 to r.
Right Right angle In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles... circular cone Cone (geometry) A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base... with radius r, height h and mass m			—
Torus Torus In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle... of tube radius a, cross-sectional radius b and mass m.		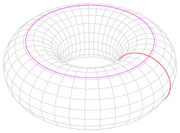About a diameter: About the vertical axis:	—
Ellipsoid (solid) of semiaxes a, b, and c with axis of rotation a and mass m			—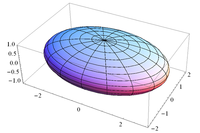
Thin rectangular plate of height h and of width w and mass m (Axis of rotation at the end of the plate)			—
Thin rectangular plate of height h and of width w and mass m			—
Solid cuboid Cuboid In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature... of height h, width w, and depth d, and mass m		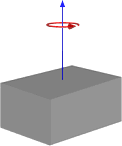	For a similarly oriented cube with sides of length , .
Solid cuboid Cuboid In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature... of height D, width W, and length L, and mass m with the longest diagonal as the axis.			For a cube with sides , .
Plane polygon Polygon In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments... with vertices , , , ..., and mass uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin.

|This expression assumes that the polygon is star-shaped

Star-shaped polygon

A star-shaped polygon is a polygonal region in the plane which is a star domain, i.e., a polygon P is star-shaped, if there exists a point z such that for each point p of P the segment zp lies entirely within P.The set of all points z with the described property is called the kernel of...

. The vectors

, ...,

are position vectors of the vertices.
|-
| Infinite disk

Disk (mathematics)

In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...

with mass normally distributed on two axes around the axis of rotation
(i.e.

Where :

is the mass-density as a function of x and y).
|align="center"|

|—
|}

See also