Schwarz reflection principle
Encyclopedia
This article is about the reflection principle in complex analysis. For the reflection principles of set theory, see Reflection principle
In mathematics
, the Schwarz reflection principle is a way to extend the domain of definition of an analytic function
of a complex variable F, which is defined on the upper half-plane and has well-defined and real number
boundary values on the real axis. In that case, writing * for complex conjugate
, the putative extension of F to the rest of the complex plane
is
or
That is, we make the definition that agrees along the real axis.
The result proved by H. A. Schwarz
is as follows. Suppose that F is a continuous function
on the closed upper half plane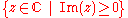
, holomorphic on the upper half plane 
, which takes real values on the real axis. Then the extension formula given above is an analytic continuation
to the whole complex plane.
In practice it would be better to have a theorem that allows F certain singularities, for example F a meromorphic function
. To understand such extensions, one needs a proof method that can be tweaked. In fact Morera's theorem
is well adapted to proving such statements. Contour integrals involving the extension of F clearly split into two, using part of the real axis. So, given that the principle is rather easy to prove in the special case from Morera's theorem, understanding the proof is enough to generate other results.
The principle also adapts to apply to harmonic function
s.
Reflection principle
In set theory, a branch of mathematics, a reflection principle says that it is possible to find sets that resemble the class of all sets. There are several different forms of the reflection principle depending on exactly what is meant by "resemble"...
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Schwarz reflection principle is a way to extend the domain of definition of an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
of a complex variable F, which is defined on the upper half-plane and has well-defined and real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
boundary values on the real axis. In that case, writing * for complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
, the putative extension of F to the rest of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
is
- F(z*)*
or
- F(z*) = F*(z).
That is, we make the definition that agrees along the real axis.
The result proved by H. A. Schwarz
Hermann Schwarz
Karl Hermann Amandus Schwarz was a German mathematician, known for his work in complex analysis. He was born in Hermsdorf, Silesia and died in Berlin...
is as follows. Suppose that F is a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on the closed upper half plane
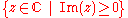, holomorphic on the upper half plane , which takes real values on the real axis. Then the extension formula given above is an analytic continuationAnalytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
to the whole complex plane.
In practice it would be better to have a theorem that allows F certain singularities, for example F a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
. To understand such extensions, one needs a proof method that can be tweaked. In fact Morera's theorem
Morera's theorem
In complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic....
is well adapted to proving such statements. Contour integrals involving the extension of F clearly split into two, using part of the real axis. So, given that the principle is rather easy to prove in the special case from Morera's theorem, understanding the proof is enough to generate other results.
The principle also adapts to apply to harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s.