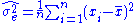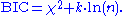Schwarz criterion
Encyclopedia
In statistics
, the Bayesian information criterion (BIC) or Schwarz criterion (also SBC, SBIC) is a criterion for model selection
among a finite set of models. It is based, in part, on the likelihood function
, and it is closely related to Akaike information criterion
(AIC).
When fitting models, it is possible to increase the likelihood by adding parameters, but doing so may result in overfitting
. The BIC resolves this problem by introducing a penalty term for the number of parameters in the model. The penalty term is larger in BIC than in AIC.
The BIC was developed by Gideon E. Schwarz, who gave a Bayesian
argument for adopting it. It is closely related to the Akaike information criterion
(AIC). In fact, Akaike was so impressed with Schwarz's Bayesian formalism that he developed his own Bayesian formalism, now often referred to as the ABIC for "a Bayesian Information Criterion" or more casually "Akaike's Bayesian Information Criterion".
. Let:
The formula for the BIC is: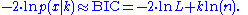
Under the assumption that the model errors or disturbances are independent and identically distributed according to a normal distribution and that the boundary condition that the derivative of the log likelihood in respect to the true variance is zero, this becomes (up to an additive constant, which depends only on n and not on the model):
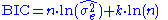
where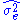
is the error variance.
The error variance in this case is defined as
One may point out from probability theory, that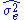
is a biased estimator for the true variance, 
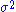. Let 
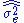denote the unbiased form of approximating the error variance. It is defined as
Additionally, under the assumption of normality the following version may be more tractable
Note that there is a constant added that follows from transition from log-likelihood to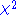
; however, in using the BIC to determine the "best" model the constant becomes trivial.
Given any two estimated models, the model with the lower value of BIC is the one to be preferred. The BIC is an increasing function
of
and an increasing function of k. That is, unexplained variation in the dependent variable and the number of explanatory variables increase the value of BIC. Hence, lower BIC implies either fewer explanatory variables, better fit, or both. The BIC generally penalizes free parameters more strongly than does the Akaike information criterion
, though it depends on the size of n and relative magnitude of n and k.
It is important to keep in mind that the BIC can be used to compare estimated models only when the numerical values of the dependent variable are identical for all estimates being compared. The models being compared need not be nested, unlike the case when models are being compared using an F or likelihood ratio test.
-based models. However, in many applications (for example, selecting a black body
or power law
spectrum for an astronomical source), BIC simply reduces to maximum likelihood selection because the number of parameters is equal for the models of interest.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Bayesian information criterion (BIC) or Schwarz criterion (also SBC, SBIC) is a criterion for model selection
Model selection
Model selection is the task of selecting a statistical model from a set of candidate models, given data. In the simplest cases, a pre-existing set of data is considered...
among a finite set of models. It is based, in part, on the likelihood function
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
, and it is closely related to Akaike information criterion
Akaike information criterion
The Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
(AIC).
When fitting models, it is possible to increase the likelihood by adding parameters, but doing so may result in overfitting
Overfitting
In statistics, overfitting occurs when a statistical model describes random error or noise instead of the underlying relationship. Overfitting generally occurs when a model is excessively complex, such as having too many parameters relative to the number of observations...
. The BIC resolves this problem by introducing a penalty term for the number of parameters in the model. The penalty term is larger in BIC than in AIC.
The BIC was developed by Gideon E. Schwarz, who gave a Bayesian
Bayesian
Bayesian refers to methods in probability and statistics named after the Reverend Thomas Bayes , in particular methods related to statistical inference:...
argument for adopting it. It is closely related to the Akaike information criterion
Akaike information criterion
The Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
(AIC). In fact, Akaike was so impressed with Schwarz's Bayesian formalism that he developed his own Bayesian formalism, now often referred to as the ABIC for "a Bayesian Information Criterion" or more casually "Akaike's Bayesian Information Criterion".
Mathematically
The BIC is an asymptotic result derived under the assumptions that the data distribution is in the exponential familyExponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
. Let:
- x = the observed data;
- n = the number of data points in x, the number of observationObservationObservation is either an activity of a living being, such as a human, consisting of receiving knowledge of the outside world through the senses, or the recording of data using scientific instruments. The term may also refer to any data collected during this activity...
s, or equivalently, the sample size; - k = the number of free parameterParameterParameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s to be estimated. If the estimated model is a linear regressionLinear regressionIn statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
, k is the number of regressors, including the intercept; - p(x|k) = the probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of the observed data given the number of parameters; or, the likelihoodLikelihoodLikelihood is a measure of how likely an event is, and can be expressed in terms of, for example, probability or odds in favor.-Likelihood function:...
of the parameters given the dataset; - L = the maximized value of the likelihoodLikelihoodLikelihood is a measure of how likely an event is, and can be expressed in terms of, for example, probability or odds in favor.-Likelihood function:...
function for the estimated model.
The formula for the BIC is:
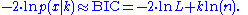
Under the assumption that the model errors or disturbances are independent and identically distributed according to a normal distribution and that the boundary condition that the derivative of the log likelihood in respect to the true variance is zero, this becomes (up to an additive constant, which depends only on n and not on the model):
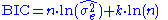
where
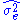is the error variance.The error variance in this case is defined as
One may point out from probability theory, that
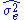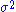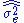is a biased estimator for the true variance, . Let denote the unbiased form of approximating the error variance. It is defined as
Additionally, under the assumption of normality the following version may be more tractable
Note that there is a constant added that follows from transition from log-likelihood to
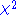; however, in using the BIC to determine the "best" model the constant becomes trivial.Given any two estimated models, the model with the lower value of BIC is the one to be preferred. The BIC is an increasing function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of
and an increasing function of k. That is, unexplained variation in the dependent variable and the number of explanatory variables increase the value of BIC. Hence, lower BIC implies either fewer explanatory variables, better fit, or both. The BIC generally penalizes free parameters more strongly than does the Akaike information criterionAkaike information criterion
The Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
, though it depends on the size of n and relative magnitude of n and k.
It is important to keep in mind that the BIC can be used to compare estimated models only when the numerical values of the dependent variable are identical for all estimates being compared. The models being compared need not be nested, unlike the case when models are being compared using an F or likelihood ratio test.
Characteristics of the Bayesian information criterion
- It is independent of the prior or the prior is "vague" (a constant).
- It can measure the efficiency of the parameterized model in terms of predicting the data.
- It penalizes the complexity of the model where complexity refers to the number of parameters in model.
- It is approximately equal to the minimum description lengthMinimum description lengthThe minimum description length principle is a formalization of Occam's Razor in which the best hypothesis for a given set of data is the one that leads to the best compression of the data. MDL was introduced by Jorma Rissanen in 1978...
criterion but with negative sign. - It can be used to choose the number of clusters according to the intrinsic complexity present in a particular dataset.
- It is closely related to other penalized likelihood criteria such as RIC and the Akaike information criterionAkaike information criterionThe Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
.
Applications
BIC has been widely used for model identification in time series and linear regression. It can, however, be applied quite widely to any set of maximum likelihoodMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
-based models. However, in many applications (for example, selecting a black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
or power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
spectrum for an astronomical source), BIC simply reduces to maximum likelihood selection because the number of parameters is equal for the models of interest.
See also
- Akaike information criterionAkaike information criterionThe Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
- Bayesian model comparison
- Deviance information criterionDeviance information criterionThe deviance information criterion is a hierarchical modeling generalization of the AIC and BIC . It is particularly useful in Bayesian model selection problems where the posterior distributions of the models have been obtained by Markov chain Monte Carlo simulation...
- Hannan–Quinn information criterion
- Jensen–Shannon divergenceJensen–Shannon divergenceIn probability theory and statistics, the Jensen–Shannon divergence is a popular method of measuring the similarity between two probability distributions. It is also known as information radius or total divergence to the average. It is based on the Kullback–Leibler divergence, with the notable ...
- Kullback–Leibler divergenceKullback–Leibler divergenceIn probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
- Model selectionModel selectionModel selection is the task of selecting a statistical model from a set of candidate models, given data. In the simplest cases, a pre-existing set of data is considered...