
Jensen–Shannon divergence
Encyclopedia
In probability theory
and statistics
, the Jensen–Shannon divergence is a popular method of measuring the similarity between two probability distribution
s. It is also known as information radius (IRad) or total divergence to the average. It is based on the Kullback–Leibler divergence
, with the notable (and useful) difference that it is always a finite value. The square root of the Jensen–Shannon divergence is a metric
.
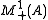 of probability distributions where A is a set provided with some σ-algebra
of probability distributions where A is a set provided with some σ-algebra
of measurable subsets. In particular we can take A to be a finite or countable set with all subsets being measurable.
The Jensen–Shannon divergence (JSD)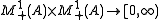 is a symmetrized and smoothed version of the Kullback–Leibler divergence
is a symmetrized and smoothed version of the Kullback–Leibler divergence
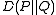 . It is defined by
. It is defined by

where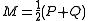
If A is countable, a more general definition, allowing for the comparison of more than two distributions, is:
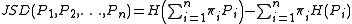
where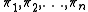 are the weights for the probability distributions
are the weights for the probability distributions 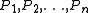 and
and  is the Shannon entropy for distribution
is the Shannon entropy for distribution 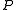 . For the two-distribution case described above,
. For the two-distribution case described above,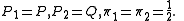
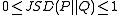
between a random variable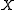 from a mixture distribution
from a mixture distribution 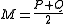 and a binary indicator variable
and a binary indicator variable 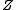 where
where 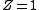 if
if 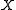 is from
is from 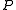 and
and 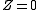 if
if 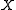 is from
is from 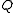 .
.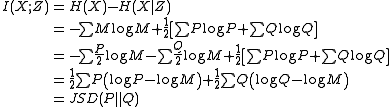
It follows from the above result that Jensen-Shannon divergence is bounded by 0 and 1 because mutual information is non-negative and bounded by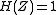 .
.
One can apply the same principle to the joint and product of marginal distribution (in analogy to Kullback-Leibler divergence and mutual information) and to measure how reliably one can decide if a given response comes from the joint distribution or the product distribution—given that these are the only possibilities.
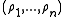 and probability distribution
and probability distribution 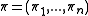 as
as
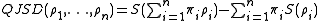
where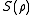 is the von Neumann entropy
is the von Neumann entropy
. This quantity was introduced in quantum information theory, where it is called the Holevo information: it gives the upper bound for amount of classical information encoded by the quantum states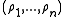 under the prior distribution
under the prior distribution  (see Holevo's theorem
(see Holevo's theorem
) Quantum Jensen–Shannon divergence for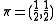 and two density matrices is a symmetric function, everywhere defined, bounded and equal to zero only if two density matrices are the same. It is a square of a metric for pure states but it is unknown whether the metric property holds in general.
and two density matrices is a symmetric function, everywhere defined, bounded and equal to zero only if two density matrices are the same. It is a square of a metric for pure states but it is unknown whether the metric property holds in general.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Jensen–Shannon divergence is a popular method of measuring the similarity between two probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s. It is also known as information radius (IRad) or total divergence to the average. It is based on the Kullback–Leibler divergence
Kullback–Leibler divergence
In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
, with the notable (and useful) difference that it is always a finite value. The square root of the Jensen–Shannon divergence is a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
.
Definition
Consider the set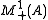 of probability distributions where A is a set provided with some σ-algebra
of probability distributions where A is a set provided with some σ-algebraSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
of measurable subsets. In particular we can take A to be a finite or countable set with all subsets being measurable.
The Jensen–Shannon divergence (JSD)
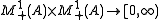 is a symmetrized and smoothed version of the Kullback–Leibler divergence
is a symmetrized and smoothed version of the Kullback–Leibler divergenceKullback–Leibler divergence
In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
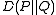 . It is defined by
. It is defined by
where
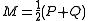
If A is countable, a more general definition, allowing for the comparison of more than two distributions, is:
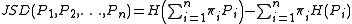
where
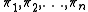 are the weights for the probability distributions
are the weights for the probability distributions 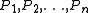 and
and  is the Shannon entropy for distribution
is the Shannon entropy for distribution 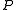 . For the two-distribution case described above,
. For the two-distribution case described above,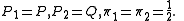
Bounds
According to Lin (1991), the Jensen–Shannon divergence is bounded by 1.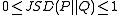
Relation to mutual information
Jensen-Shannon divergence is the mutual informationMutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
between a random variable
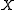 from a mixture distribution
from a mixture distribution 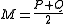 and a binary indicator variable
and a binary indicator variable 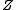 where
where 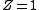 if
if 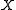 is from
is from 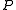 and
and 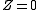 if
if 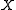 is from
is from 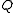 .
.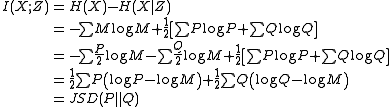
It follows from the above result that Jensen-Shannon divergence is bounded by 0 and 1 because mutual information is non-negative and bounded by
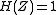 .
.One can apply the same principle to the joint and product of marginal distribution (in analogy to Kullback-Leibler divergence and mutual information) and to measure how reliably one can decide if a given response comes from the joint distribution or the product distribution—given that these are the only possibilities.
Quantum Jensen-Shannon divergence
The generalization of probability distributions on density matrices allows to define quantum Jensen–Shannon divergence (QJSD). It is defined for a set of density matrices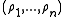 and probability distribution
and probability distribution 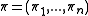 as
as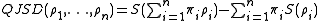
where
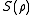 is the von Neumann entropy
is the von Neumann entropyVon Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
. This quantity was introduced in quantum information theory, where it is called the Holevo information: it gives the upper bound for amount of classical information encoded by the quantum states
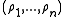 under the prior distribution
under the prior distribution  (see Holevo's theorem
(see Holevo's theoremHolevo's theorem
In physics, in the area of quantum information theory, Holevo's theorem is an important limitative theorem in quantum computing which was published by in 1973....
) Quantum Jensen–Shannon divergence for
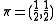 and two density matrices is a symmetric function, everywhere defined, bounded and equal to zero only if two density matrices are the same. It is a square of a metric for pure states but it is unknown whether the metric property holds in general.
and two density matrices is a symmetric function, everywhere defined, bounded and equal to zero only if two density matrices are the same. It is a square of a metric for pure states but it is unknown whether the metric property holds in general.
