
Minimum description length
Encyclopedia
The minimum description length (MDL) principle is a formalization of Occam's Razor
in which the best hypothesis
for a given set of data is the one that leads to the best compression of the data
. MDL was introduced by Jorma Rissanen
in 1978. It is an important concept in information theory
and learning theory
.
) alphabet
.
To select the hypothesis that captures the most regularity in the data, scientists look for the hypothesis with which the best compression can be achieved. In order to do this, a code
is fixed to compress the data, most generally with a (Turing-complete) computer
language
. A program
to output the data is written in that language; thus the program effectively represents the data. The length of the shortest program that outputs the data is called the Kolmogorov complexity
of the data. This is the central idea of Ray Solomonoff's
idealized theory of inductive inference
.
MDL attempts to remedy these, by:
Rather than "programs", in MDL theory one usually speaks of candidate hypotheses, models or codes. The set of allowed codes is then called the model class. (Some authors refer to the model class as the model.) The code is then selected for which the sum of the description of the code and the description of the data using the code is minimal.
One of the important properties of MDL methods is that they provide a natural safeguard against overfitting
, because they implement a tradeoff between the complexity of the hypothesis (model class) and the complexity of the data given the hypothesis .
For this reason a naive statistical method might choose the second model as a better explanation for the data. However, an MDL approach would construct a single code based on the hypothesis, instead of just using the best one. To do this, it is simplest to use a two-part code in which the element of the model class with the best performance is specified. Then the data is specified using that code. A lot of bits are needed to specify which code to use; thus the total codelength based on the second model class could be larger than 1,000 bits. Therefore the conclusion when following an MDL approach is inevitably that there is not enough evidence to support the hypothesis of the biased coin, even though the best element of the second model class provides better fit to the data.
and probability distribution
s. (This follows from the Kraft-McMillan inequality.) For any probability distribution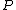 , it is possible to construct a code
, it is possible to construct a code 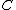 such that the length (in bits) of
such that the length (in bits) of 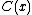 is equal to
is equal to 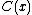 ; this code minimizes the expected code length. Vice versa, given a code
; this code minimizes the expected code length. Vice versa, given a code 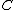 , one can construct a probability distribution
, one can construct a probability distribution 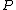 such that the same holds. (Rounding issues are ignored here.) In other words, searching for an efficient code reduces to searching for a good probability distribution, and vice versa.
such that the same holds. (Rounding issues are ignored here.) In other words, searching for an efficient code reduces to searching for a good probability distribution, and vice versa.
and statistics
through the correspondence between codes and probability distributions mentioned above. This has led researchers such as David MacKay to view MDL as equivalent to Bayesian inference
: code length of the model and code length of model and data together in MDL correspond to prior probability
and marginal likelihood
respectively in the Bayesian framework.
While Bayesian machinery is often useful in constructing efficient MDL codes, the MDL framework also accommodates other codes that are not Bayesian. An example is the Shtarkov normalized maximum likelihood code, which plays a central role in current MDL theory, but has no equivalent in Bayesian inference. Furthermore, Rissanen stresses that we should make no assumptions about the true data generating process
: in practice, a model class is typically a simplification of reality and thus does not contain any code or probability distribution that is true in any objective sense.. In the last mentioned reference Rissanen bases the mathematical underpinning of MDL on the Kolmogorov structure function
.
According to the MDL philosophy, Bayesian methods should be dismissed if they are based on unsafe priors
that would lead to poor results. The priors that are acceptable from an MDL point of view also tend to be favored in so-called objective Bayesian analysis; there, however, the motivation is usually different.
approach to learning; as early as 1968 Wallace and Boulton pioneered a related concept called Minimum Message Length
(MML). The difference between MDL and MML is a source of ongoing confusion. Superficially, the methods appear mostly equivalent, but there are some significant differences, especially in interpretation:
Occam's razor
Occam's razor, also known as Ockham's razor, and sometimes expressed in Latin as lex parsimoniae , is a principle that generally recommends from among competing hypotheses selecting the one that makes the fewest new assumptions.-Overview:The principle is often summarized as "simpler explanations...
in which the best hypothesis
Hypothesis
A hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
for a given set of data is the one that leads to the best compression of the data
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
. MDL was introduced by Jorma Rissanen
Jorma Rissanen
Jorma J. Rissanen is an information theorist, known for inventing the arithmetic coding technique of lossless data compression, and the minimum description length principle....
in 1978. It is an important concept in information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
and learning theory
Learning theory
Learning theory may refer to:* Learning theory , the process of how humans learn** Behaviorism** Cognitivism** Constructivism** Connectivism* Computational learning theory, a mathematical theory to analyze machine learning algorithms...
.
Overview
Any set of data can be represented by a string of symbols from a finite (say, binaryBinary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
) alphabet
Alphabet
An alphabet is a standard set of letters—basic written symbols or graphemes—each of which represents a phoneme in a spoken language, either as it exists now or as it was in the past. There are other systems, such as logographies, in which each character represents a word, morpheme, or semantic...
.
The fundamental idea behind the MDL Principle is that any regularity in a given set of data can be used to compress the dataData compressionIn computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
, i.e. to describe it using fewer symbols than needed to describe the data literally." (Grünwald, 1998)
To select the hypothesis that captures the most regularity in the data, scientists look for the hypothesis with which the best compression can be achieved. In order to do this, a code
Code
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
is fixed to compress the data, most generally with a (Turing-complete) computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
. A program
Computer program
A computer program is a sequence of instructions written to perform a specified task with a computer. A computer requires programs to function, typically executing the program's instructions in a central processor. The program has an executable form that the computer can use directly to execute...
to output the data is written in that language; thus the program effectively represents the data. The length of the shortest program that outputs the data is called the Kolmogorov complexity
Kolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
of the data. This is the central idea of Ray Solomonoff's
Ray Solomonoff
Ray Solomonoff was the inventor of algorithmic probability, and founder of algorithmic information theory, He was an originator of the branch of artificial intelligence based on machine learning, prediction and probability...
idealized theory of inductive inference
Inductive inference
Around 1960, Ray Solomonoff founded the theory of universal inductive inference, the theory of prediction based on observations; for example, predicting the next symbol based upon a given series of symbols...
.
Inference
However, this mathematical theory does not provide a practical way of reaching an inference. The most important reasons for this are:- Kolmogorov complexity is uncomputableComputability theoryComputability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
: there exists no algorithm that, when input an arbitrary sequence of data, outputs the shortest program that produces the data. - Kolmogorov complexity depends on what computer language is used. This is an arbitrary choice, but it does influence the complexity up to some constant additive term. For that reason, constant terms tend to be disregarded in Kolmogorov complexity theory. In practice, however, where often only a small amount of data is available, such constants may have a very large influence on the inference results: good results cannot be guaranteed when one is working with limited data.
MDL attempts to remedy these, by:
- Restricting the set of allowed codes in such a way that it becomes possible (computable) to find the shortest codelength of the data, relative to the allowed codes, and
- Choosing a code that is reasonably efficient, whatever the data at hand. This point is somewhat elusive and much research is still going on in this area.
Rather than "programs", in MDL theory one usually speaks of candidate hypotheses, models or codes. The set of allowed codes is then called the model class. (Some authors refer to the model class as the model.) The code is then selected for which the sum of the description of the code and the description of the data using the code is minimal.
One of the important properties of MDL methods is that they provide a natural safeguard against overfitting
Overfitting
In statistics, overfitting occurs when a statistical model describes random error or noise instead of the underlying relationship. Overfitting generally occurs when a model is excessively complex, such as having too many parameters relative to the number of observations...
, because they implement a tradeoff between the complexity of the hypothesis (model class) and the complexity of the data given the hypothesis .
Example of MDL
A coin is flipped 1,000 times and the numbers of heads and tails are recorded. Consider two model classes:- The first is a code that represents outcomes with a 0 for heads or a 1 for tails. This code represents the hypothesis that the coin is fair. The code length according to this code is always exactly 1,000 bits.
- The second consists of all codes that are efficient for a coin with some specific bias, representing the hypothesis that the coin is not fair. Say that we observe 510 heads and 490 tails. Then the code length according to the best code in the second model class is shorter than 1,000 bits.
For this reason a naive statistical method might choose the second model as a better explanation for the data. However, an MDL approach would construct a single code based on the hypothesis, instead of just using the best one. To do this, it is simplest to use a two-part code in which the element of the model class with the best performance is specified. Then the data is specified using that code. A lot of bits are needed to specify which code to use; thus the total codelength based on the second model class could be larger than 1,000 bits. Therefore the conclusion when following an MDL approach is inevitably that there is not enough evidence to support the hypothesis of the biased coin, even though the best element of the second model class provides better fit to the data.
MDL Notation
Central to MDL theory is the one-to-one correspondence between code length functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
and probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s. (This follows from the Kraft-McMillan inequality.) For any probability distribution
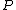 , it is possible to construct a code
, it is possible to construct a code 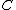 such that the length (in bits) of
such that the length (in bits) of 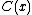 is equal to
is equal to 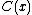 ; this code minimizes the expected code length. Vice versa, given a code
; this code minimizes the expected code length. Vice versa, given a code 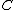 , one can construct a probability distribution
, one can construct a probability distribution 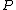 such that the same holds. (Rounding issues are ignored here.) In other words, searching for an efficient code reduces to searching for a good probability distribution, and vice versa.
such that the same holds. (Rounding issues are ignored here.) In other words, searching for an efficient code reduces to searching for a good probability distribution, and vice versa.Related concepts
MDL is very strongly connected to probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
through the correspondence between codes and probability distributions mentioned above. This has led researchers such as David MacKay to view MDL as equivalent to Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
: code length of the model and code length of model and data together in MDL correspond to prior probability
Prior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
and marginal likelihood
Marginal likelihood
In statistics, a marginal likelihood function, or integrated likelihood, is a likelihood function in which some parameter variables have been marginalised...
respectively in the Bayesian framework.
While Bayesian machinery is often useful in constructing efficient MDL codes, the MDL framework also accommodates other codes that are not Bayesian. An example is the Shtarkov normalized maximum likelihood code, which plays a central role in current MDL theory, but has no equivalent in Bayesian inference. Furthermore, Rissanen stresses that we should make no assumptions about the true data generating process
Data generating process
The term data generating process is used in statistical and scientific literature to convey a number of different ideas:*the data collection process, being routes and procedures by which data reach a database ;...
: in practice, a model class is typically a simplification of reality and thus does not contain any code or probability distribution that is true in any objective sense.. In the last mentioned reference Rissanen bases the mathematical underpinning of MDL on the Kolmogorov structure function
Kolmogorov structure function
In 1974 Kolmogorov proposed a non-probabilistic approach to statistics and model selection. Let each data be a finite binary string and models be finite sets of binary strings...
.
According to the MDL philosophy, Bayesian methods should be dismissed if they are based on unsafe priors
Prior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
that would lead to poor results. The priors that are acceptable from an MDL point of view also tend to be favored in so-called objective Bayesian analysis; there, however, the motivation is usually different.
Other Systems
MDL was not the first information-theoreticInformation theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
approach to learning; as early as 1968 Wallace and Boulton pioneered a related concept called Minimum Message Length
Minimum message length
Minimum message length is a formal information theory restatement of Occam's Razor: even when models are not equal in goodness of fit accuracy to the observed data, the one generating the shortest overall message is more likely to be correct...
(MML). The difference between MDL and MML is a source of ongoing confusion. Superficially, the methods appear mostly equivalent, but there are some significant differences, especially in interpretation:
- MML is a fully subjective Bayesian approach: it starts from the idea that one represents one's beliefs about the data generating process in the form of a prior distribution. MDL avoids assumptions about the data generating process.
- Both methods make use of two-part codes: the first part always represents the information that one is trying to learn, such as the index of a model class (model selectionModel selectionModel selection is the task of selecting a statistical model from a set of candidate models, given data. In the simplest cases, a pre-existing set of data is considered...
), or parameter values (parameter estimation); the second part is an encoding of the data given the information in the first part. The difference between the methods is that, in the MDL literature, it is advocated that unwanted parameters should be moved to the second part of the code, where they can be represented with the data by using a so-called one-part code, which is often more efficient than a two-part code. In the original description of MML, all parameters are encoded in the first part, so all parameters are learned.
Further reading
- Minimum Description Length on the Web, by the University of Helsinki. Features readings, demonstrations, events and links to MDL researchers.
- Homepage of Jorma Rissanen, containing lecture notes and other recent material on MDL.
- Homepage of Peter Grünwald, containing his very good tutorial on MDL.
- J. Rissanen, Information and Complexity in Statistical Modeling, Springer, 2007.
- ISBN0-262-07262-9.
- David MacKayDavid MacKay (scientist)David John Cameron MacKay, FRS, is the professor of natural philosophy in the department of Physics at the University of Cambridge and chief scientific adviser to the UK Department of Energy and Climate Change...
, Information Theory, Inference, and Learning Algorithms, Cambridge University Press, 2003.

