Sample mean and sample covariance
Encyclopedia
The sample mean or empirical mean and the sample covariance are statistic
s computed from a collection of data on one or more random variables. The sample mean is a vector each of whose elements is the sample mean of one of the random variables that is, each of whose elements is the average of the observed values of one of the variables. The sample covariance is a square matrix
whose i, j element is the covariance between the sets of observed values of two of the variables and whose i, i element is the variance of the observed values of one of the variables. If only one variable has had values observed, then the sample mean is a single number (the average of the observed values of that variable) and the covariance matrix is also simply a single value (the variance of the observed values of that variable).
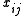be the ith independently drawn observation (i=1,...,N) on the jth random variable (j=1,...,K), and arrange them in an N × K matrix, with row i denoted 
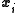(i=1,...,N).
The sample mean vector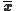
is a row vector whose jth element (j = 1, ..., K) is the average value of the N observations on the jth random variable. Thus the sample mean vector is the average of the row vectors of observations on the K variables:
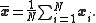
Here the individual element j of the sample mean vector, the mean of the jth random variable, is
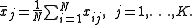
The sample covariance of N observations on the K variables is the K-by-K matrix
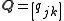with the entries given by
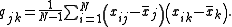
The sample mean and the sample covariance matrix are unbiased estimates
of the mean
and the covariance matrix
of the random vector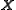
, a row vector whose jth element (j = 1, ..., K) is one of the random variables. The sample covariance matrix has 
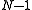in the denominator rather than 
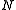due to a variant of Bessel's correction
: In short, the sample covariance relies on the difference between each observation and the sample mean, but the sample mean is slightly correlated with each observation since it's defined in terms of all observations. If the population mean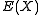
is known, the analogous unbiased estimate
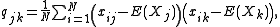
using the population mean, has
in the denominator. This is an example of why in probability and statistics it is essential to distinguish between upper case letters (random variable
s) and lower case letters (realizations
of the random variables).
The maximum likelihood
estimate of the covariance
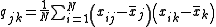
for the Gaussian distribution case has N in the denominator as well. The ratio of 1/N to 1/(N − 1) approaches 1 for large N, so the maximum likelihood estimate approximately equals the unbiased estimate when the sample is large.
of the population mean, as its expected value is the same as the random variable's population mean, but it is not exact: different samples drawn from the same distribution will give different sample means and hence different estimates of the mean of the random variable's population
. Thus the sample mean is a random variable
, not a constant, and consequently it will have its own distribution. For a random sample of N observations on the jth random variable, the sample mean's distribution itself has mean equal to the population mean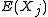
and variance equal to 
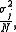where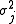 
is the variance of the random variable Xj.
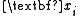(each set of single observations on each of the K random variables) is assigned a weight 
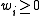. Without loss of generality, assume that the weights are normalized
:
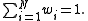
(If they are not, divide the weights by their sum.)
Then the weighted mean
vector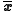
and the weighted covariance matrix 
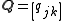are given by
Therefore, in the most general case
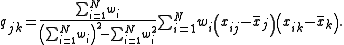
If all weights are the same,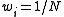
, the weighted mean and covariance reduce to the sample mean and covariance above.
, respectively, likely the most common: they are easily calculated and possess desirable characteristics.
However, they suffer from certain drawbacks; notably, they are not robust statistics
, meaning that they are sensitive to outliers. As robustness is often a desired trait, particularly in real-world applications, robust alternatives may prove desirable, notably quantile
-based statistics such the sample median for location, and interquartile range
(IQR) for dispersion. Other alternatives include trimming
and Winsorising
, as in the trimmed mean and the Winsorized mean
.
Statistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
s computed from a collection of data on one or more random variables. The sample mean is a vector each of whose elements is the sample mean of one of the random variables that is, each of whose elements is the average of the observed values of one of the variables. The sample covariance is a square matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
whose i, j element is the covariance between the sets of observed values of two of the variables and whose i, i element is the variance of the observed values of one of the variables. If only one variable has had values observed, then the sample mean is a single number (the average of the observed values of that variable) and the covariance matrix is also simply a single value (the variance of the observed values of that variable).
Sample mean and covariance
Let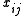 be the ith independently drawn observation (i=1,...,N) on the jth random variable (j=1,...,K), and arrange them in an N × K matrix, with row i denoted 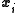(i=1,...,N).The sample mean vector
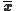is a row vector whose jth element (j = 1, ..., K) is the average value of the N observations on the jth random variable. Thus the sample mean vector is the average of the row vectors of observations on the K variables: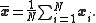Here the individual element j of the sample mean vector, the mean of the jth random variable, is
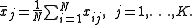
The sample covariance of N observations on the K variables is the K-by-K matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
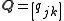with the entries given by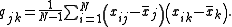The sample mean and the sample covariance matrix are unbiased estimates
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
of the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and the covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of the random vector
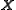, a row vector whose jth element (j = 1, ..., K) is one of the random variables. The sample covariance matrix has 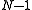in the denominator rather than 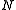due to a variant of Bessel's correctionBessel's correction
In statistics, Bessel's correction, named after Friedrich Bessel, is the use of n − 1 instead of n in the formula for the sample variance and sample standard deviation, where n is the number of observations in a sample: it corrects the bias in the estimation of the population variance,...
: In short, the sample covariance relies on the difference between each observation and the sample mean, but the sample mean is slightly correlated with each observation since it's defined in terms of all observations. If the population mean
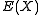is known, the analogous unbiased estimate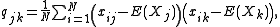using the population mean, has
in the denominator. This is an example of why in probability and statistics it is essential to distinguish between upper case letters (random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s) and lower case letters (realizations
Realization (probability)
In probability and statistics, a realization, or observed value, of a random variable is the value that is actually observed . The random variable itself should be thought of as the process how the observation comes about...
of the random variables).
The maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimate of the covariance
Estimation of covariance matrices
In statistics, sometimes the covariance matrix of a multivariate random variable is not known but has to be estimated. Estimation of covariance matrices then deals with the question of how to approximate the actual covariance matrix on the basis of a sample from the multivariate distribution...
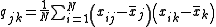
for the Gaussian distribution case has N in the denominator as well. The ratio of 1/N to 1/(N − 1) approaches 1 for large N, so the maximum likelihood estimate approximately equals the unbiased estimate when the sample is large.
Variance of the sample mean
For each random variable, the sample mean makes a good estimatorEstimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
of the population mean, as its expected value is the same as the random variable's population mean, but it is not exact: different samples drawn from the same distribution will give different sample means and hence different estimates of the mean of the random variable's population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
. Thus the sample mean is a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, not a constant, and consequently it will have its own distribution. For a random sample of N observations on the jth random variable, the sample mean's distribution itself has mean equal to the population mean
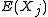and variance equal to 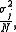where 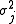is the variance of the random variable Xj.Weighted samples
In a weighted sample, each vector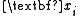 (each set of single observations on each of the K random variables) is assigned a weight 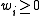. Without loss of generality, assume that the weights are normalizedNormalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
:
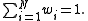
(If they are not, divide the weights by their sum.)
Then the weighted mean
Weighted mean
The weighted mean is similar to an arithmetic mean , where instead of each of the data points contributing equally to the final average, some data points contribute more than others...
vector
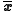and the weighted covariance matrix 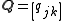are given byTherefore, in the most general case
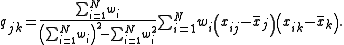
If all weights are the same,
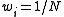, the weighted mean and covariance reduce to the sample mean and covariance above.Criticism
The sample mean and sample covariance are widely used in statistics and applications, and are extremely common measures of location and dispersionStatistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
, respectively, likely the most common: they are easily calculated and possess desirable characteristics.
However, they suffer from certain drawbacks; notably, they are not robust statistics
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
, meaning that they are sensitive to outliers. As robustness is often a desired trait, particularly in real-world applications, robust alternatives may prove desirable, notably quantile
Quantile
Quantiles are points taken at regular intervals from the cumulative distribution function of a random variable. Dividing ordered data into q essentially equal-sized data subsets is the motivation for q-quantiles; the quantiles are the data values marking the boundaries between consecutive subsets...
-based statistics such the sample median for location, and interquartile range
Interquartile range
In descriptive statistics, the interquartile range , also called the midspread or middle fifty, is a measure of statistical dispersion, being equal to the difference between the upper and lower quartiles...
(IQR) for dispersion. Other alternatives include trimming
Trimmed estimator
Given an estimator, a trimmed estimator is obtained by excluding some of the extreme values. This is generally done to obtain a more robust statistic: the extreme values are considered outliers....
and Winsorising
Winsorising
Winsorising or Winsorization is the transformation of statistics by limiting extreme values in the statistical data to reduce the effect of possibly spurious outliers. It is named after the engineer-turned-biostatistician Charles P. Winsor...
, as in the trimmed mean and the Winsorized mean
Winsorized mean
A Winsorized mean is a Winsorized statistical measure of central tendency, much like the mean and median, and even more similar to the truncated mean...
.
See also
- Unbiased estimation of standard deviationUnbiased estimation of standard deviationThe question of unbiased estimation of a standard deviation arises in statistics mainly as question in statistical theory. Except in some important situations, outlined later, the task has little relevance to applications of statistics since its need is avoided by standard procedures, such as the...
- Estimation of covariance matricesEstimation of covariance matricesIn statistics, sometimes the covariance matrix of a multivariate random variable is not known but has to be estimated. Estimation of covariance matrices then deals with the question of how to approximate the actual covariance matrix on the basis of a sample from the multivariate distribution...
- Scatter matrixScatter matrixIn multivariate statistics and probability theory, the scatter matrix is a statistic that is used to make estimates of the covariance matrix of the multivariate normal distribution.-Definition:...