Scatter matrix
Encyclopedia
In multivariate statistics
and probability theory
, the scatter matrix is a statistic
that is used to make estimates
of the covariance matrix
of the multivariate normal distribution.
, the sample mean is
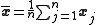
where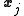
is the jth column of 
.
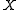The scatter matrix is the m-by-m positive semi-definite matrix
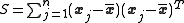
where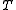
denotes matrix transpose. The scatter matrix may be expressed more succinctly as
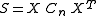
where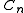
is the n-by-n centering matrix
.
estimate, given n samples, for the covariance matrix of a multivariate normal distribution can be expressed as the normalized scatter matrix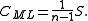
When the columns of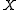
are independently sampled from a multivariate normal distribution, then 
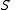has a Wishart distribution.
Multivariate statistics
Multivariate statistics is a form of statistics encompassing the simultaneous observation and analysis of more than one statistical variable. The application of multivariate statistics is multivariate analysis...
and probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the scatter matrix is a statistic
Statistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
that is used to make estimates
Estimation of covariance matrices
In statistics, sometimes the covariance matrix of a multivariate random variable is not known but has to be estimated. Estimation of covariance matrices then deals with the question of how to approximate the actual covariance matrix on the basis of a sample from the multivariate distribution...
of the covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of the multivariate normal distribution.
Definition
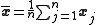
Given n samples of m-dimensional data, represented as the m-by-n matrix,, the sample mean iswhere
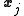is the jth column of 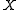.The scatter matrix is the m-by-m positive semi-definite matrix
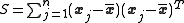
where
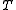denotes matrix transpose. The scatter matrix may be expressed more succinctly as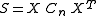where
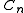is the n-by-n centering matrixCentering matrix
In mathematics and multivariate statistics, the centering matrix is a symmetric and idempotent matrix, which when multiplied with a vector has the same effect as subtracting the mean of the components of the vector from every component.- Definition :...
.
Application
The maximum likelihoodMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimate, given n samples, for the covariance matrix of a multivariate normal distribution can be expressed as the normalized scatter matrix
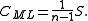
When the columns of
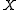are independently sampled from a multivariate normal distribution, then 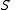has a Wishart distribution.See also
- Estimation of covariance matricesEstimation of covariance matricesIn statistics, sometimes the covariance matrix of a multivariate random variable is not known but has to be estimated. Estimation of covariance matrices then deals with the question of how to approximate the actual covariance matrix on the basis of a sample from the multivariate distribution...
- Sample covariance matrix
- Wishart distribution
- Outer productOuter productIn linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
—
is the outer product of X with itself.