
Weighted mean
Encyclopedia
The weighted mean is similar to an arithmetic mean
(the most common type of average
), where instead of each of the data points contributing equally to the final average, some data points contribute more than others. The notion of weighted mean plays a role in descriptive statistics
and also occurs in a more general form in several other areas of mathematics.
If all the weights are equal, then the weighted mean is the same as the arithmetic mean
. While weighted means generally behave in a similar fashion to arithmetic means, they do have a few counter-intuitive properties, as captured for instance in Simpson's paradox
.
The term weighted average usually refers to a weighted arithmetic mean, but weighted versions of other means can also be calculated, such as the weighted geometric mean and the weighted harmonic mean.
The straight average for the morning class is 80 and the straight average of the afternoon class is 90. The straight average of 80 and 90 is 85, the mean of the two class means. However, this does not account for the difference in number of students in each class, and the value of 85 does not reflect the average student grade (independent of class). The average student grade can be obtained by averaging all the grades, without regard to classes:

Or, this can be accomplished by weighting the class means by the number of students in each class (using a weighted mean of the class means):

Thus, the weighted mean makes it possible to find the average student grade in the case where only the class means and the number of students in each class are available.

with non-negative weights
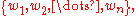
is the quantity

which means:

Therefore data elements with a high weight contribute more to the weighted mean than do elements with a low weight. The weights cannot be negative. Some may be zero, but not all of them (since division by zero is not allowed).
The formulas are simplified when the weights are normalized such that they sum up to , i.e.
, i.e.  . For such normalized weights the weighted mean is simply
. For such normalized weights the weighted mean is simply
 .
.
The common mean is a special case of the weighted mean where all data have equal weights,
is a special case of the weighted mean where all data have equal weights,  . When the weights are normalized then
. When the weights are normalized then 
 , a distance variable.
, a distance variable.
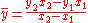
.
Using the previous example, we would get the following:

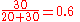

This simplifies to:

 , with normalized weights (weights summing to one) is itself a random variable. Its expected value and standard deviation are related to the expected values and standard deviations of the observations as follows.
, with normalized weights (weights summing to one) is itself a random variable. Its expected value and standard deviation are related to the expected values and standard deviations of the observations as follows.
If the observations have expected values
then the weighted sample mean has expectation
Particularly, if the expectations of all observations are equal,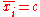 , then the expectation of the weighted sample mean will be the same,
, then the expectation of the weighted sample mean will be the same,
For uncorrelated observations with standard deviations , the weighted sample mean has standard deviation
, the weighted sample mean has standard deviation
Consequently, when the standard deviations of all observations are equal, , the weighted sample mean will have standard deviation
, the weighted sample mean will have standard deviation  . Here
. Here  is the quantity
is the quantity
such that . It attains its minimum value for equal weights, and its maximum when all weights except one are zero. In the former case we have
. It attains its minimum value for equal weights, and its maximum when all weights except one are zero. In the former case we have  , which is related to the central limit theorem
, which is related to the central limit theorem
.
 comes from a different probability distribution
comes from a different probability distribution
with known variance
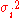 , one possible choice for the weights is given by:
, one possible choice for the weights is given by:

The weighted mean in this case is:
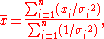
and the variance of the weighted mean is:

which reduces to , when all
, when all 
The significance of this choice is that this weighted mean is the maximum likelihood estimator of the mean of the probability distributions under the assumption that they are independent and normally distributed with the same mean.
Correcting for over- or under-dispersion
Weighted means are typically used to find the weighted mean of experimental data, rather than theoretically generated data. In this case, there will be some error in the variance of each data point. Typically experimental errors may be underestimated due to the experimenter not taking into account all sources of error in calculating the variance of each data point. In this event, the variance in the weighted mean must be corrected to account for the fact that  is too large. The correction that must be made is
is too large. The correction that must be made is

where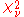 is
is  divided by the number of degrees of freedom, in this case n − 1. This gives the variance in the weighted mean as:
divided by the number of degrees of freedom, in this case n − 1. This gives the variance in the weighted mean as:

and standard deviation
about that mean. When a weighted mean is used, the variance of the weighted sample is different from the variance of the unweighted sample. The biased weighted sample variance is defined similarly to the normal biased sample variance:
is used, the variance of the weighted sample is different from the variance of the unweighted sample. The biased weighted sample variance is defined similarly to the normal biased sample variance:


where , which is 1 for normalized weights.
, which is 1 for normalized weights.
For small samples, it is customary to use an unbiased estimator for the population variance. In normal unweighted samples, the N in the denominator (corresponding to the sample size) is changed to N − 1. While this is simple in unweighted samples, it is not straightforward when the sample is weighted. The unbiased estimator of a weighted population variance (assuming each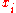 is drawn from a Gaussian distribution with variance
is drawn from a Gaussian distribution with variance  ) is given by :
) is given by :

where as introduced previously.
as introduced previously.
The degrees of freedom of the weighted, unbiased sample variance vary accordingly from N − 1 down to 0.
The standard deviation is simply the square root of the variance above.
If all of the are drawn from the same distribution and the integer weights
are drawn from the same distribution and the integer weights  indicate frequency of occurrence in the sample, then the unbiased estimator of the weighted population variance is given by
indicate frequency of occurrence in the sample, then the unbiased estimator of the weighted population variance is given by

If all are unique, then
are unique, then  counts the number of unique values, and
counts the number of unique values, and  counts the number of samples.
counts the number of samples.
For example, if values are drawn from the same distribution, then we can treat this set as an unweighted sample, or we can treat it as the weighted sample
are drawn from the same distribution, then we can treat this set as an unweighted sample, or we can treat it as the weighted sample  with corresponding weights
with corresponding weights  , and we should get the same results.
, and we should get the same results.
estimate. We simply replace by the covariance matrix:
by the covariance matrix:

The weighted mean in this case is:
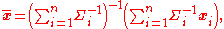
and the covariance of the weighted mean is:

For example, consider the weighted mean of the point [1 0] with high variance in the second component and [0 1] with high variance in the first component. Then

then the weighted mean is: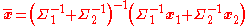
which makes sense: the [1 0] estimate is "compliant" in the second component and the [0 1] estimate is compliant in the first component, so the weighted mean is nearly [1 1].
 ,
,  is the covariance matrix
is the covariance matrix
relating the quantities ,
,  is the common mean to be estimated, and
is the common mean to be estimated, and  is the design matrix
is the design matrix
[1, ..., 1] (of length ). The Gauss–Markov theorem
). The Gauss–Markov theorem
states that the estimate of the mean having minimum variance is given by:

and

 and a dependent variable
and a dependent variable  , with
, with  observations sampled at discrete times
observations sampled at discrete times  . In many common situations, the value of
. In many common situations, the value of  at time
at time  depends not only on
depends not only on  but also on its past values. Commonly, the strength of this dependence decreases as the separation of observations in time increases. To model this situation, one may replace the independent variable by its sliding mean
but also on its past values. Commonly, the strength of this dependence decreases as the separation of observations in time increases. To model this situation, one may replace the independent variable by its sliding mean  for a window size
for a window size  .
.

 at each time step. Setting
at each time step. Setting  we can define
we can define  normalized weights by
normalized weights by
where is the sum of the unnormalized weights. In this case
is the sum of the unnormalized weights. In this case  is simply
is simply
approaching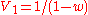 for large values of
for large values of  .
.
The damping constant must correspond to the actual decrease of interaction strength. If this cannot be determined from theoretical considerations, then the following properties of exponentially decreasing weights are useful in making a suitable choice: at step
must correspond to the actual decrease of interaction strength. If this cannot be determined from theoretical considerations, then the following properties of exponentially decreasing weights are useful in making a suitable choice: at step  , the weight approximately equals
, the weight approximately equals 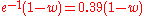 , the tail area the value
, the tail area the value  , the head area
, the head area 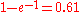 . The tail area at step
. The tail area at step  is
is  . Where primarily the closest
. Where primarily the closest  observations matter and the effect of the remaining observations can be ignored safely, then choose
observations matter and the effect of the remaining observations can be ignored safely, then choose  such that the tail area is sufficiently small.
such that the tail area is sufficiently small.
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
(the most common type of average
Average
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
), where instead of each of the data points contributing equally to the final average, some data points contribute more than others. The notion of weighted mean plays a role in descriptive statistics
Descriptive statistics
Descriptive statistics quantitatively describe the main features of a collection of data. Descriptive statistics are distinguished from inferential statistics , in that descriptive statistics aim to summarize a data set, rather than use the data to learn about the population that the data are...
and also occurs in a more general form in several other areas of mathematics.
If all the weights are equal, then the weighted mean is the same as the arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
. While weighted means generally behave in a similar fashion to arithmetic means, they do have a few counter-intuitive properties, as captured for instance in Simpson's paradox
Simpson's paradox
In probability and statistics, Simpson's paradox is a paradox in which a correlation present in different groups is reversed when the groups are combined. This result is often encountered in social-science and medical-science statistics, and it occurs when frequencydata are hastily given causal...
.
The term weighted average usually refers to a weighted arithmetic mean, but weighted versions of other means can also be calculated, such as the weighted geometric mean and the weighted harmonic mean.
Example
Given two school classes, one with 20 students, and one with 30 students, the grades in each class on a test were:- Morning class = 62, 67, 71, 74, 76, 77, 78, 79, 79, 80, 80, 81, 81, 82, 83, 84, 86, 89, 93, 98
- Afternoon class = 81, 82, 83, 84, 85, 86, 87, 87, 88, 88, 89, 89, 89, 90, 90, 90, 90, 91, 91, 91, 92, 92, 93, 93, 94, 95, 96, 97, 98, 99
The straight average for the morning class is 80 and the straight average of the afternoon class is 90. The straight average of 80 and 90 is 85, the mean of the two class means. However, this does not account for the difference in number of students in each class, and the value of 85 does not reflect the average student grade (independent of class). The average student grade can be obtained by averaging all the grades, without regard to classes:

Or, this can be accomplished by weighting the class means by the number of students in each class (using a weighted mean of the class means):

Thus, the weighted mean makes it possible to find the average student grade in the case where only the class means and the number of students in each class are available.
Mathematical definition
Formally, the weighted mean of a non-empty set of data
with non-negative weights
Weight function
A weight function is a mathematical device used when performing a sum, integral, or average in order to give some elements more "weight" or influence on the result than other elements in the same set. They occur frequently in statistics and analysis, and are closely related to the concept of a...
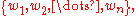
is the quantity

which means:

Therefore data elements with a high weight contribute more to the weighted mean than do elements with a low weight. The weights cannot be negative. Some may be zero, but not all of them (since division by zero is not allowed).
The formulas are simplified when the weights are normalized such that they sum up to
 , i.e.
, i.e.  . For such normalized weights the weighted mean is simply
. For such normalized weights the weighted mean is simply .
.The common mean
 is a special case of the weighted mean where all data have equal weights,
is a special case of the weighted mean where all data have equal weights,  . When the weights are normalized then
. When the weights are normalized then 
Length-weighted mean
This is used for weighting a response variable based upon its dependency on , a distance variable.
, a distance variable.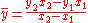
Convex combination
Since only the relative weights are relevant, any weighted mean can be expressed using coefficients that sum to one. Such a linear combination is called a convex combinationConvex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
.
Using the previous example, we would get the following:

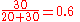

This simplifies to:

Statistical properties
The weighted sample mean, , with normalized weights (weights summing to one) is itself a random variable. Its expected value and standard deviation are related to the expected values and standard deviations of the observations as follows.
, with normalized weights (weights summing to one) is itself a random variable. Its expected value and standard deviation are related to the expected values and standard deviations of the observations as follows.If the observations have expected values
then the weighted sample mean has expectation
Particularly, if the expectations of all observations are equal,
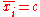 , then the expectation of the weighted sample mean will be the same,
, then the expectation of the weighted sample mean will be the same,
For uncorrelated observations with standard deviations
 , the weighted sample mean has standard deviation
, the weighted sample mean has standard deviation
Consequently, when the standard deviations of all observations are equal,
 , the weighted sample mean will have standard deviation
, the weighted sample mean will have standard deviation  . Here
. Here  is the quantity
is the quantity
such that
 . It attains its minimum value for equal weights, and its maximum when all weights except one are zero. In the former case we have
. It attains its minimum value for equal weights, and its maximum when all weights except one are zero. In the former case we have  , which is related to the central limit theorem
, which is related to the central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
.
Dealing with variance
For the weighted mean of a list of data for which each element comes from a different probability distribution
comes from a different probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
with known variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
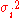 , one possible choice for the weights is given by:
, one possible choice for the weights is given by:
The weighted mean in this case is:
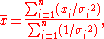
and the variance of the weighted mean is:

which reduces to
 , when all
, when all 
The significance of this choice is that this weighted mean is the maximum likelihood estimator of the mean of the probability distributions under the assumption that they are independent and normally distributed with the same mean.
Correcting for over- or under-dispersionOverdispersionIn statistics, overdispersion is the presence of greater variability in a data set than would be expected based on a given simple statistical model....
Weighted means are typically used to find the weighted mean of experimental data, rather than theoretically generated data. In this case, there will be some error in the variance of each data point. Typically experimental errors may be underestimated due to the experimenter not taking into account all sources of error in calculating the variance of each data point. In this event, the variance in the weighted mean must be corrected to account for the fact that  is too large. The correction that must be made is
is too large. The correction that must be made is
where
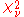 is
is  divided by the number of degrees of freedom, in this case n − 1. This gives the variance in the weighted mean as:
divided by the number of degrees of freedom, in this case n − 1. This gives the variance in the weighted mean as:
Weighted sample variance
Typically when a mean is calculated it is important to know the varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
and standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
about that mean. When a weighted mean
 is used, the variance of the weighted sample is different from the variance of the unweighted sample. The biased weighted sample variance is defined similarly to the normal biased sample variance:
is used, the variance of the weighted sample is different from the variance of the unweighted sample. The biased weighted sample variance is defined similarly to the normal biased sample variance:

where
 , which is 1 for normalized weights.
, which is 1 for normalized weights.For small samples, it is customary to use an unbiased estimator for the population variance. In normal unweighted samples, the N in the denominator (corresponding to the sample size) is changed to N − 1. While this is simple in unweighted samples, it is not straightforward when the sample is weighted. The unbiased estimator of a weighted population variance (assuming each
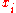 is drawn from a Gaussian distribution with variance
is drawn from a Gaussian distribution with variance  ) is given by :
) is given by :
where
 as introduced previously.
as introduced previously.The degrees of freedom of the weighted, unbiased sample variance vary accordingly from N − 1 down to 0.
The standard deviation is simply the square root of the variance above.
If all of the
 are drawn from the same distribution and the integer weights
are drawn from the same distribution and the integer weights  indicate frequency of occurrence in the sample, then the unbiased estimator of the weighted population variance is given by
indicate frequency of occurrence in the sample, then the unbiased estimator of the weighted population variance is given by
If all
 are unique, then
are unique, then  counts the number of unique values, and
counts the number of unique values, and  counts the number of samples.
counts the number of samples.For example, if values
 are drawn from the same distribution, then we can treat this set as an unweighted sample, or we can treat it as the weighted sample
are drawn from the same distribution, then we can treat this set as an unweighted sample, or we can treat it as the weighted sample  with corresponding weights
with corresponding weights  , and we should get the same results.
, and we should get the same results.Vector-valued estimates
The above generalizes easily to the case of taking the mean of vector-valued estimates. For example, estimates of position on a plane may have less certainty in one direction than another. As in the scalar case, the weighted mean of multiple estimates can provide a maximum likelihoodMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimate. We simply replace
 by the covariance matrix:
by the covariance matrix:
The weighted mean in this case is:
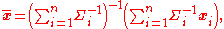
and the covariance of the weighted mean is:

For example, consider the weighted mean of the point [1 0] with high variance in the second component and [0 1] with high variance in the first component. Then


then the weighted mean is:
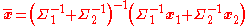
which makes sense: the [1 0] estimate is "compliant" in the second component and the [0 1] estimate is compliant in the first component, so the weighted mean is nearly [1 1].
Accounting for correlations
In the general case, suppose that ,
,  is the covariance matrix
is the covariance matrixCovariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
relating the quantities
 ,
,  is the common mean to be estimated, and
is the common mean to be estimated, and  is the design matrix
is the design matrixDesign matrix
In statistics, a design matrix is a matrix of explanatory variables, often denoted by X, that is used in certain statistical models, e.g., the general linear model....
[1, ..., 1] (of length
 ). The Gauss–Markov theorem
). The Gauss–Markov theoremGauss–Markov theorem
In statistics, the Gauss–Markov theorem, named after Carl Friedrich Gauss and Andrey Markov, states that in a linear regression model in which the errors have expectation zero and are uncorrelated and have equal variances, the best linear unbiased estimator of the coefficients is given by the...
states that the estimate of the mean having minimum variance is given by:

and

Decreasing strength of interactions
Consider the time series of an independent variable and a dependent variable
and a dependent variable 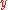 , with
, with  observations sampled at discrete times
observations sampled at discrete times  . In many common situations, the value of
. In many common situations, the value of  at time
at time  depends not only on
depends not only on  but also on its past values. Commonly, the strength of this dependence decreases as the separation of observations in time increases. To model this situation, one may replace the independent variable by its sliding mean
but also on its past values. Commonly, the strength of this dependence decreases as the separation of observations in time increases. To model this situation, one may replace the independent variable by its sliding mean  for a window size
for a window size  .
.
| Range (1–5) | Weighted mean equivalence |
|---|---|
| 3.34–5.00 | Strong |
| 1.67–3.33 | Satisfactory |
| 0.00–1.66 | Weak |
Exponentially decreasing weights
In the scenario described in the previous section, most frequently the decrease in interaction strength obeys a negative exponential law. If the observations are sampled at equidistant times, then exponential decrease is equivalent to decrease by a constant fraction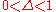 at each time step. Setting
at each time step. Setting  we can define
we can define  normalized weights by
normalized weights by
-
 ,
,
where
 is the sum of the unnormalized weights. In this case
is the sum of the unnormalized weights. In this case  is simply
is simply
-
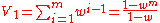 ,
,
approaching
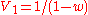 for large values of
for large values of  .
.The damping constant
 must correspond to the actual decrease of interaction strength. If this cannot be determined from theoretical considerations, then the following properties of exponentially decreasing weights are useful in making a suitable choice: at step
must correspond to the actual decrease of interaction strength. If this cannot be determined from theoretical considerations, then the following properties of exponentially decreasing weights are useful in making a suitable choice: at step  , the weight approximately equals
, the weight approximately equals 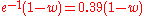 , the tail area the value
, the tail area the value  , the head area
, the head area 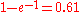 . The tail area at step
. The tail area at step  is
is  . Where primarily the closest
. Where primarily the closest  observations matter and the effect of the remaining observations can be ignored safely, then choose
observations matter and the effect of the remaining observations can be ignored safely, then choose  such that the tail area is sufficiently small.
such that the tail area is sufficiently small.Weighted averages of functions
The concept of weighted average can be extended to functions. Weighted averages of functions play an important role in the systems of weighted differential and integral calculus.See also
- AverageAverageIn mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
- MeanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
- Summary statisticsSummary statisticsIn descriptive statistics, summary statistics are used to summarize a set of observations, in order to communicate the largest amount as simply as possible...
- Central tendencyCentral tendencyIn statistics, the term central tendency relates to the way in which quantitative data is clustered around some value. A measure of central tendency is a way of specifying - central value...
- Weight functionWeight functionA weight function is a mathematical device used when performing a sum, integral, or average in order to give some elements more "weight" or influence on the result than other elements in the same set. They occur frequently in statistics and analysis, and are closely related to the concept of a...
- Weighted least squares
- Weighted average cost of capitalWeighted average cost of capitalThe weighted average cost of capital is the rate that a company is expected to pay on average to all its security holders to finance its assets....
- WeightingWeightingThe process of weighting involves emphasizing the contribution of some aspects of a phenomenon to a final effect or result — giving them 'more weight' in the analysis. That is, rather than each variable in the data contributing equally to the final result, some data are adjusted to contribute...
- Weighted geometric mean
- Weighted harmonic mean
- Standard DeviationStandard deviationStandard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
Further reading
- Bevington, Philip. Data Reduction and Error Analysis for the Physical Sciences.







