Angular eccentricity
Encyclopedia
In the study of ellipse
s and related geometry, various parameters in the distortion of a circle into an ellipse are identified and employed: Aspect ratio, flattening
and eccentricity
.
All of these parameters are ultimately trigonometric functions of the ellipse's modular angle, or angular eccentricity, the conventional denotation being the Greek letter "alpha
",
.
, or transverse radius,
, and semi-minor axis
, or conjugate radius,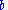
, is defined as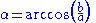
and 
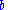will be utilized.
! name !! value in terms of
and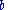 
!! value in terms of 
|-
| aspect ratio ||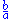
|| 
|}
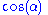
is actually a trio of factors: The primary, or first, eccentricity,
, (or just "
"), the second eccentricity, 
, and the third eccentricity, 
or 
.
! symbol !! value in terms of
and 
!! value in terms of 
|-
|
|| 
|| 
|-
|
|| 
|| 
|-
|
|| 
|| 
|}
Since they are mostly used in that form anyway, the eccentricities are usually found and kept in their squared form.
The primary eccentricity could be regarded as the complementary aspect ratio, as it is the ratio of the linear eccentricity to the semi-major axis:
, or ellipticity, in contrast, is self-explanatory, as it defines the degree of "squashing", from no flattening (a perfect circle) to complete flattening (a straight line).
! symbol !! value in terms of
and 
!! value in terms of 
|-
|
|| 
|| 
|-
|
|| 
|| 
|-
|
|| 
|| 
|}
While the aspect ratio would seem to be the ideal parameter to find an unknown axis (usually
), it is usually the inverse (primary) flattening that is provided:
, or prolatum; rotation about the minor axis produces an oblate spheroid, or oblatum.
Rotation causes most large celestial bodies – stars, planets and large satellites – to form oblate spheroids. Planetodetic formulation therefore applies the oblate format, which follows standard elliptic parametrization.
, 
, and 
. However, these parameters don't provide the clear and obvious transformational relationships and structure. Consider the basic elliptic integrand at point P:
While one may consider such ability to convert as just gratuitously frivolous, there is at least one valid reason, as the Binomial series expansion
(which planetodetic formularies frequently use) for
converges a lot quicker than the one for 
which, in turn, converges quicker than 
's (which—in line with basic, series expansion theory—doesn't even converge when 
≥ 1). Friedrich Bessel
firstly used the notation "n" in 1837 on calculation of meridian arc
length.
Furthermore, as
, there are likely other, even more efficient, series expansions possible (if not even efficiently practical approximations to a general transcendental
elliptic integral
).
Another example is the equation for authalic surface area:
While one certainly can use
to define and express this type of equation, using 
frequently provides a more illustrative—if not even its definitively mathematical—origin.
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s and related geometry, various parameters in the distortion of a circle into an ellipse are identified and employed: Aspect ratio, flattening
Flattening
The flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator...
and eccentricity
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
.
All of these parameters are ultimately trigonometric functions of the ellipse's modular angle, or angular eccentricity, the conventional denotation being the Greek letter "alpha
Alpha
Alpha is the first letter of the Greek alphabet. Alpha or ALPHA may also refer to:-Science:*Alpha , the highest ranking individuals in a community of social animals...
",
.Definition
The angular eccentricity of an ellipse with semi-major axisSemi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
, or transverse radius,
, and semi-minor axisSemi-minor axis
In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...
, or conjugate radius,
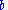, is defined as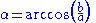Elliptic parameters
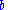In the following, the previously defined ellipse with radii and will be utilized.Aspect ratio
The most tangible characteristic of an ellipse is the diametric quotient of the minor axis to the major axis, the aspect ratio.-
- {| class="wikitable"
! name !! value in terms of
and 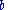!! value in terms of |-
| aspect ratio ||
|| |}
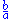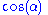
Eccentricity
The eccentricityEccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
is actually a trio of factors: The primary, or first, eccentricity,
, (or just ""), the second eccentricity, , and the third eccentricity, or .-
- {| class="wikitable"
! symbol !! value in terms of
and !! value in terms of |-
|
|| || |-
|
|| || |-
|
|| || |}
Since they are mostly used in that form anyway, the eccentricities are usually found and kept in their squared form.
The primary eccentricity could be regarded as the complementary aspect ratio, as it is the ratio of the linear eccentricity to the semi-major axis:
Flattening
The flatteningFlattening
The flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator...
, or ellipticity, in contrast, is self-explanatory, as it defines the degree of "squashing", from no flattening (a perfect circle) to complete flattening (a straight line).
-
- {| class="wikitable"
! symbol !! value in terms of
and !! value in terms of |-
|
|| || |-
|
|| || |-
|
|| || |}
While the aspect ratio would seem to be the ideal parameter to find an unknown axis (usually
), it is usually the inverse (primary) flattening that is provided:Oblate vs. prolate
If an ellipse is rotated about one of its axes, it sweeps an ellipsoid of revolution. Rotation about the major axis produces a prolate spheroidProlate spheroid
A prolate spheroid is a spheroid in which the polar axis is greater than the equatorial diameter. Prolate spheroids stand in contrast to oblate spheroids...
, or prolatum; rotation about the minor axis produces an oblate spheroid, or oblatum.
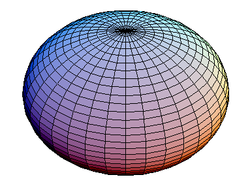← Oblate; Prolate →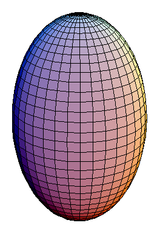 
Rotation causes most large celestial bodies – stars, planets and large satellites – to form oblate spheroids. Planetodetic formulation therefore applies the oblate format, which follows standard elliptic parametrization.
Applications
For the most part, elliptic formularies ignore the angular eccentricity for the more familiar and notationally concise, , and . However, these parameters don't provide the clear and obvious transformational relationships and structure. Consider the basic elliptic integrand at point P:While one may consider such ability to convert as just gratuitously frivolous, there is at least one valid reason, as the Binomial series expansion
Binomial series
In mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f = α, where is an arbitrary complex number...
(which planetodetic formularies frequently use) for
converges a lot quicker than the one for which, in turn, converges quicker than 's (which—in line with basic, series expansion theory—doesn't even converge when ≥ 1). Friedrich BesselFriedrich Bessel
-References:* John Frederick William Herschel, A brief notice of the life, researches, and discoveries of Friedrich Wilhelm Bessel, London: Barclay, 1847 -External links:...
firstly used the notation "n" in 1837 on calculation of meridian arc
Meridian arc
In geodesy, a meridian arc measurement is a highly accurate determination of the distance between two points with the same longitude. Two or more such determinations at different locations then specify the shape of the reference ellipsoid which best approximates the shape of the geoid. This...
length.
Furthermore, as
, there are likely other, even more efficient, series expansions possible (if not even efficiently practical approximations to a general transcendentalTranscendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
).
Another example is the equation for authalic surface area:
While one certainly can use
to define and express this type of equation, using frequently provides a more illustrative—if not even its definitively mathematical—origin.