Radiation stress
Encyclopedia
In fluid dynamics
, the radiation stress is the depth-integrated – and thereafter phase
-average
d – excess momentum flux
caused by the presence of the surface gravity waves, which is exerted on the mean flow
. The radiation stresses behave as a second-order tensor
.
The radiation stress tensor describes the additional forcing
due to the presence of the waves, which changes the mean depth-integrated horizontal momentum
in the fluid layer. As a result, varying radiation stresses induce changes in the mean surface elevation (wave setup
) and the mean flow (wave-induced currents).
For the mean energy density
in the oscillatory part
of the fluid motion, the radiation stress tensor is important for its dynamics
, in case of an inhomogeneous mean-flow field
.
The radiation stress tensor, as well as several of its implications on the physics of surface gravity waves and mean flows, were formulated in a series of papers by Longuet-Higgins
and Stewart in 1960–1964.
Radiation stress derives its name from the analogous effect of radiation pressure
for electromagnetic radiation
.
importance is Sxx. It is defined as:
where p(x,z,t) is the fluid pressure
, u(x,z,t) is the horizontal x-component of the oscillatory part
of the flow velocity
vector
, z is the vertical coordinate, t is time, z = −h(x) is the bed elevation of the fluid layer, and z = η(x,t) is the surface elevation. Further ρ is the fluid density
and g is the acceleration by gravity
, while an overbar denotes phase
averaging
. The last term on the right-hand side, ½ρg(h+)2, is the integral
of the hydrostatic pressure over the still-water depth.
To lowest (second) order, the radiation stress Sxx for traveling periodic waves can be determined from the properties of surface gravity waves according to Airy wave theory
:
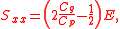
where Cp is the phase speed and Cg is the group speed of the waves. Further E is the mean depth-integrated wave energy density (the sum of the kinetic
and potential energy
) per unit of horizontal area. From the results of Airy wave theory, to second order, the mean energy density E equals:
with a the wave amplitude
and H = 2a the wave height
. Note this equation is for periodic waves: in random waves the root-mean-square wave height Hrms should be used with Hrms = Hm0 / √2, where Hm0 is the significant wave height
. Then E = ρgHm02.
is a second-order tensor
with components:
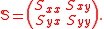
With, in a cartesian coordinate system
(x,y,z):
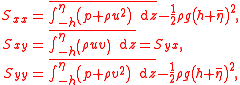
where u and v are the horizontal x- and y-components of the oscillatory part u(x,y,z,t) of the flow velocity vector.
To second order – in wave amplitude a – the components of the radiation stress tensor for progressive periodic waves are:
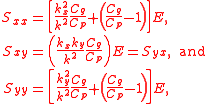
where kx and ky are the x- and y-components of the wavenumber
vector k, with length k = |k| = and the vector k perpendicular to the wave crests
. The phase and group speeds, Cp and Cg respectively, are the lengths of the phase and group velocity vectors: Cp = |Cp| and Cg = |Cg|.
in the wave propagation direction, also called the wave (pseudo) momentum
. To lowest order, the wave momentum Mw is, per unit of horizontal area:
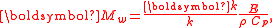
which is exact for progressive waves of permanent form in irrotational flow. Above, Cp is the phase speed relative to the mean flow:
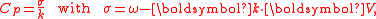
with σ the intrinsic angular frequency, as seen by an observer moving with the mean flow V while ω is the apparent angular frequency of an observer at rest (with respect to 'Earth'). The difference k⋅V is the Doppler shift.
The mean momentum M, also per unit of horizontal area, is the mean value of the integral of momentum over depth:
with v(x,y,z,t) the total flow velocity at any point below the free surface z = η(x,y,t).
Now the mass transport velocity U is defined as:
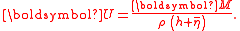
Observe that first the depth-integrated horizontal momentum is averaged, before the division by the mean water depth (h+) is made.
:
with U including the contribution of the wave momentum Mw.
The equation for the conservation of horizontal mean momentum is:
where U ⊗ U denotes the tensor product
of U with itself, and τw is the mean wind shear stress
at the free surface, while τb is the bed shear stress. Note that the right hand side of the momentum equation provides the non-conservative contributions of the bed slope ∇h, as well the forcing by the wind and the bed friction.
In terms of the horizontal momentum M the above equations become:
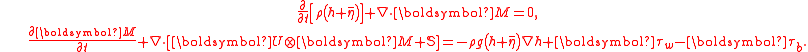
, the mass conservation equation becomes:
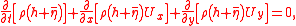
with Ux and Uy respectively the x and y components of the mass transport velocity U.
The horizontal momentum equations are:
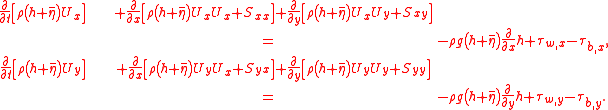
the mean mechanical energy
of the total flow – that is the sum of the energy of the mean flow and the fluctuating motion – is conserved. However, the mean energy of the fluctuating motion itself is not conserved, nor is the energy of the mean flow. The mean energy E of the fluctuating motion (the sum of the kinetic
and potential energies
satisfies:
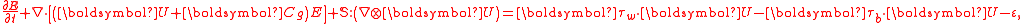
where ":" denotes the double-dot product
, and ε denotes the dissipation of mean mechanical energy (for instance by wave breaking). The term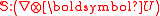
is the exchange of energy with the mean motion, due to wave–current interaction
. The mean horizontal wave-energy transport (U + Cg) E consists of two contributions:
In a cartesian coordinate system, the above equation for the mean energy E of the flow fluctuations becomes:
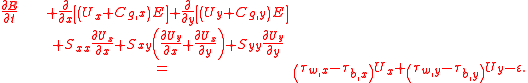
So the radiation stress changes the wave energy E only in case of a spatial-inhomogeneous
current field (Ux,Uy).
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the radiation stress is the depth-integrated – and thereafter phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
-average
Average
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
d – excess momentum flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
caused by the presence of the surface gravity waves, which is exerted on the mean flow
Mean flow
In fluid dynamics, the fluid flow is often decomposed into a mean flow – and deviations from the mean. The averaging can be done either in space or in time....
. The radiation stresses behave as a second-order tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
.
The radiation stress tensor describes the additional forcing
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
due to the presence of the waves, which changes the mean depth-integrated horizontal momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
in the fluid layer. As a result, varying radiation stresses induce changes in the mean surface elevation (wave setup
Wave setup
In fluid dynamics, wave setup is the change in mean water level due to the presence of waves. This setup is primarily present in and near the coastal surf zone...
) and the mean flow (wave-induced currents).
For the mean energy density
Energy density
Energy density is a term used for the amount of energy stored in a given system or region of space per unit volume. Often only the useful or extractable energy is quantified, which is to say that chemically inaccessible energy such as rest mass energy is ignored...
in the oscillatory part
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
of the fluid motion, the radiation stress tensor is important for its dynamics
Dynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
, in case of an inhomogeneous mean-flow field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
.
The radiation stress tensor, as well as several of its implications on the physics of surface gravity waves and mean flows, were formulated in a series of papers by Longuet-Higgins
Michael S. Longuet-Higgins
Michael Selwyn Longuet-Higgins FRS is a mathematician and oceanographer at Institute for Nonlinear Science, University of California, San Diego. He is the younger brother of H...
and Stewart in 1960–1964.
Radiation stress derives its name from the analogous effect of radiation pressure
Radiation pressure
Radiation pressure is the pressure exerted upon any surface exposed to electromagnetic radiation. If absorbed, the pressure is the power flux density divided by the speed of light...
for electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
.
Physical significance
The radiation stress – mean excess momentum-flux due to the presence of the waves – plays an important role in the explanation and modeling of various coastal processes:- Wave setup and setdown – the radiation stress consists in part of a radiation pressureRadiation pressureRadiation pressure is the pressure exerted upon any surface exposed to electromagnetic radiation. If absorbed, the pressure is the power flux density divided by the speed of light...
, exerted at the free surfaceFree surfaceIn physics, a free surface is the surface of a fluid that is subject to constant perpendicular normal stress and zero parallel shear stress,such as the boundary between two homogenous fluids,for example liquid water and the air in the Earth's atmosphere...
elevation of the mean flow. If the radiation stress varies spatially, as it does in the surf zoneSurf zoneAs ocean surface waves come closer to shore they break, forming the foamy, bubbly surface we call surf. The region of breaking waves defines the surf zone. After breaking in the surf zone, the waves continue to move in, and they run up onto the sloping front of the beach, forming an uprush of...
where the wave heightWave heightIn fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighbouring trough. Wave height is a term used by mariners, as well as in coastal, ocean and naval engineering....
reduces by wave breaking, this results in changes of the mean surface elevation called wave setup (in case of an increased level) and setdown (for a decreased water level); - Wave-driven current, especially a longshore current in the surf zone – for oblique incidence of waves on a beach, the reduction in wave height inside the surf zone (by breaking) introduces a variation of the shear-stress component Sxy of the radiation stress over the width of the surf zone. This provides the forcing of a wave-driven longshore current, which is of importance for sediment transportSediment transportSediment transport is the movement of solid particles , typically due to a combination of the force of gravity acting on the sediment, and/or the movement of the fluid in which the sediment is entrained...
(longshore driftLongshore driftLongshore drift consists of the transportation of sediments along a coast at an angle to the shoreline, which is dependent on prevailing wind direction, swash and backwash. This process occurs in the littoral zone, and in or within close proximity to the surf zone...
) and the resulting coastal morphologyGeomorphologyGeomorphology is the scientific study of landforms and the processes that shape them...
; - Bound long waves or forced long waves – for wave groups the radiation stress varies along the group. As a result, a non-linear long wave propagates together with the group, at the group velocityGroup velocityThe group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
of the modulated short waves within the group. While, according to the dispersion relationDispersion (water waves)In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
, a long wave of this length should propagate at its own – higher – phase velocityPhase velocityThe phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
. The amplitudeAmplitudeAmplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of this bound long wave varies with the square of the wave height, and is only significant in shallow water; - Wave–current interactionWave–current interactionIn fluid dynamics, wave–current interaction is the interaction between surface gravity waves and a mean flow. The interaction implies an exchange of energy, so after the start of the interaction both the waves and the mean flow are affected....
– in varying mean-flowMean flowIn fluid dynamics, the fluid flow is often decomposed into a mean flow – and deviations from the mean. The averaging can be done either in space or in time....
fieldsField (physics)In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
, the energy exchanges between the waves and the mean flow, as well as the mean-flow forcing, can be modeled by means of the radiation stress.
One-dimensional wave propagation
For uni-directional wave propagation – say in the x-coordinate direction – the component of the radiation stress tensor of dynamicalDynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
importance is Sxx. It is defined as:
where p(x,z,t) is the fluid pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, u(x,z,t) is the horizontal x-component of the oscillatory part
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
of the flow velocity
Flow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
vector
Vector (mathematics and physics)
In mathematics and physics, a vector is an element of a vector space. If n is a non negative integer and K is either the field of the real numbers or the field of the complex number, then K^n is naturally endowed with a structure of vector space, where K^n is the set of the ordered sequences of n...
, z is the vertical coordinate, t is time, z = −h(x) is the bed elevation of the fluid layer, and z = η(x,t) is the surface elevation. Further ρ is the fluid density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
and g is the acceleration by gravity
Earth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
, while an overbar denotes phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
averaging
Average
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
. The last term on the right-hand side, ½ρg(h+)2, is the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of the hydrostatic pressure over the still-water depth.
To lowest (second) order, the radiation stress Sxx for traveling periodic waves can be determined from the properties of surface gravity waves according to Airy wave theory
Airy wave theory
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational...
:
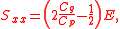
where Cp is the phase speed and Cg is the group speed of the waves. Further E is the mean depth-integrated wave energy density (the sum of the kinetic
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
and potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
) per unit of horizontal area. From the results of Airy wave theory, to second order, the mean energy density E equals:
with a the wave amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
and H = 2a the wave height
Wave height
In fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighbouring trough. Wave height is a term used by mariners, as well as in coastal, ocean and naval engineering....
. Note this equation is for periodic waves: in random waves the root-mean-square wave height Hrms should be used with Hrms = Hm0 / √2, where Hm0 is the significant wave height
Significant wave height
In physical oceanography, the significant wave height is defined traditionally as the mean wave height of the highest third of the waves , but now usually defined as four times the standard deviation of the surface elevation...
. Then E = ρgHm02.
Two-dimensional wave propagation
For wave propagation in two horizontal dimensions the radiation stress is a second-order tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
with components:
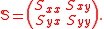
With, in a cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
(x,y,z):
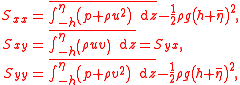
where u and v are the horizontal x- and y-components of the oscillatory part u(x,y,z,t) of the flow velocity vector.
To second order – in wave amplitude a – the components of the radiation stress tensor for progressive periodic waves are:
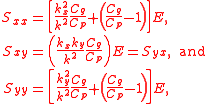
where kx and ky are the x- and y-components of the wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
vector k, with length k = |k| = and the vector k perpendicular to the wave crests
Crest (physics)
A crest is the point on a wave with the maximum value or upward displacement within a cycle. A trough is the opposite of a crest, so the minimum or lowest point in a cycle.-Interference:...
. The phase and group speeds, Cp and Cg respectively, are the lengths of the phase and group velocity vectors: Cp = |Cp| and Cg = |Cg|.
Dynamical significance
The radiation stress tensor is an important quantity in the description of the phase-averaged dynamical interaction between waves and mean flows. Here, the depth-integrated dynamical conservation equations are given, but – in order to model three-dimensional mean flows forced, or interacting with, surface waves – a three-dimensional description of the radiation stress over the fluid layer is needed.Mass transport velocity
Propagating waves induce a – relatively small – mean mass transportMass flux
Mass flux is the rate of mass flow across a unit area .-See also:*Flux*Fick's law*Darcy's law...
in the wave propagation direction, also called the wave (pseudo) momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
. To lowest order, the wave momentum Mw is, per unit of horizontal area:
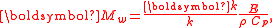
which is exact for progressive waves of permanent form in irrotational flow. Above, Cp is the phase speed relative to the mean flow:
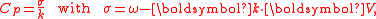
with σ the intrinsic angular frequency, as seen by an observer moving with the mean flow V while ω is the apparent angular frequency of an observer at rest (with respect to 'Earth'). The difference k⋅V is the Doppler shift.
The mean momentum M, also per unit of horizontal area, is the mean value of the integral of momentum over depth:
with v(x,y,z,t) the total flow velocity at any point below the free surface z = η(x,y,t).
Now the mass transport velocity U is defined as:
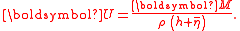
Observe that first the depth-integrated horizontal momentum is averaged, before the division by the mean water depth (h+) is made.
Vector notation
The equation of mean mass conservation is, in vector notationVector notation
This page is an overview of the common notations used when working with vectors, which may be spatial or more abstract members of vector spaces....
:
with U including the contribution of the wave momentum Mw.
The equation for the conservation of horizontal mean momentum is:
where U ⊗ U denotes the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of U with itself, and τw is the mean wind shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
at the free surface, while τb is the bed shear stress. Note that the right hand side of the momentum equation provides the non-conservative contributions of the bed slope ∇h, as well the forcing by the wind and the bed friction.
In terms of the horizontal momentum M the above equations become:
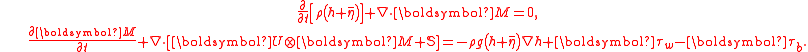
Component form in cartesian coordinates
In a cartesian coordinate systemCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, the mass conservation equation becomes:
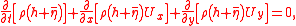
with Ux and Uy respectively the x and y components of the mass transport velocity U.
The horizontal momentum equations are:
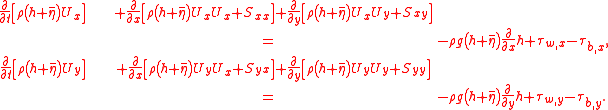
Energy conservation
For a inviscid flowInviscid flow
In fluid dynamics there are problems that are easily solved by using the simplifying assumption of an ideal fluid that has no viscosity. The flow of a fluid that is assumed to have no viscosity is called inviscid flow....
the mean mechanical energy
Mechanical energy
In physics, mechanical energy is the sum of potential energy and kinetic energy present in the components of a mechanical system. It is the energy associated with the motion and position of an object. The law of conservation of energy states that in an isolated system that is only subject to...
of the total flow – that is the sum of the energy of the mean flow and the fluctuating motion – is conserved. However, the mean energy of the fluctuating motion itself is not conserved, nor is the energy of the mean flow. The mean energy E of the fluctuating motion (the sum of the kinetic
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
and potential energies
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
satisfies:
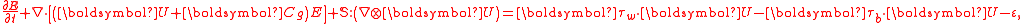
where ":" denotes the double-dot product
Dyadics
Dyadics are mathematical objects, representing linear functions of vectors. Dyadic notation was first established by Gibbs in 1884.-Definition:Dyad A is formed by two vectors a and b...
, and ε denotes the dissipation of mean mechanical energy (for instance by wave breaking). The term
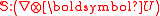is the exchange of energy with the mean motion, due to wave–current interactionWave–current interaction
In fluid dynamics, wave–current interaction is the interaction between surface gravity waves and a mean flow. The interaction implies an exchange of energy, so after the start of the interaction both the waves and the mean flow are affected....
. The mean horizontal wave-energy transport (U + Cg) E consists of two contributions:
- U E : the transport of wave energy by the mean flow, and
- Cg E : the mean energy transport by the waves themselves, with the group velocityGroup velocityThe group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
Cg as the wave-energy transport velocity.
In a cartesian coordinate system, the above equation for the mean energy E of the flow fluctuations becomes:
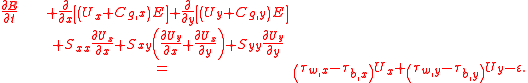
So the radiation stress changes the wave energy E only in case of a spatial-inhomogeneous
Homogeneity and heterogeneity
Homogeneity and heterogeneity are concepts relating to the uniformity or lack thereof in a substance. A material that is homogeneous is uniform in composition or character; one that is heterogeneous lacks uniformity in one of these qualities....
current field (Ux,Uy).