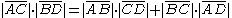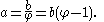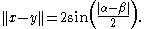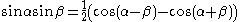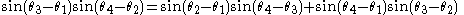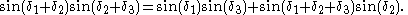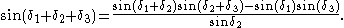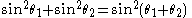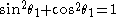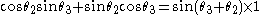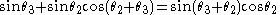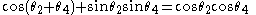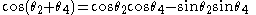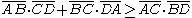Ptolemy's theorem
Encyclopedia
In Euclidean geometry
, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral
(a quadrilateral whose vertices lie on a common circle). The theorem is named after the Greek
astronomer
and mathematician
Ptolemy
(Claudius Ptolemaeus). Ptolemy used the theorem as an aid to creating his table of chords
, a trigonometric table that he applied to astronomy.
If the quadrilateral is given with its four vertices A, B, C, and D in order, then the theorem states that:
where the vertical lines denote the lengths of the line segments between the named vertices.
This relation may be verbally expressed as follows:
Moreover, the converse of Ptolemy's theorem is also true:
Given An equilateral triangle inscribed on a circle and a point on the circle.
The distance from the point to the most distant vertex of the triangle is the sum of the distances from the point to the two nearer vertices.
Proof: Follows immediately from Ptolemy's theorem:
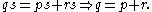
can be inscribed in a circle whose center is the barycenter of the square. If the common length of its four sides is equal to
then the length of the diagonal is equal to 
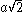according to the Pythagorean theorem
and the relation obviously holds.
with sides a and b and diagonal d then Ptolemy's theorem reduces to the Pythagorean theorem. In this case the center of the circle coincides with the point of intersection of the diagonals. The product of the diagonals is then d2, the right hand side of Ptolemy's relation is the sum a2 + b2.
Copernicus − who used Ptolemy's theorem extensively in his trigonometrical work − refers to this result as a 'Porism' or self evident corollary:
De Revolutionibus Orbium Coelestium: Page 37. See last two lines of this page.
Nor for that matter does Copernicus refer to "Ptolemy's Theorem" but labels it more simply as "Theorema Secundum".
A more interesting example is the relation between the length a of the side and the (common) length b of the 5 chords in a regular pentagon. In this case the relation reads b2 = a2 + ab which yields the golden ratio
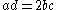
where 
is the golden ratio.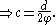
whence the side of the inscribed decagon is obtained in terms of the circle diameter. Pythagoras' Theorem applied to right triangle AFD then yields "b" in terms of the diameter and "a" the side of the pentagon is thereafter calculated as
As Copernicus (following Ptolemy) wrote,
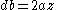
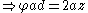where 
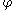is the golden ratio.
z subtends 540 at the circumference, c (the side of the decagon) subtends 180 at the circumference and thereby is established:
and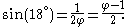 
And since angle ABF is subtended by the diameter and is therefore right, the side of the pentagon is calculated by an even simpler route:
Based on his circle of diameter 200000 units, Copernicus provides accurate numerical values for the four pentagon related chords corresponding to these angles:
Golden ratio aficionados will instantly recognize the digits 161803 and 61803 as corresponding to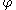
and its reciprocal. The chords are of considerable historical importance because, along with the sides of the triangle and tetragon (square), they enable the generation of a table of half chords (effectively sine values) which in turn underpins many of the key astronomical measurements and calculations effected by Copernicus in the development of his helio-centric model:
Therefore
where r is the radius of the circle and also the side of the inscribed hexagon.
Whence with relative ease is proved Proposition 10 in Book XIII of Euclid's Elements: The square on the side of the pentagon equals the sum of the squares on the sides of the hexagon and the decagon inscribed in the same circle.
In modern trigonometric notation this corresponds to the identity:
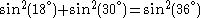
The Pythagorean nature of this relationship makes possible the construction of a regular pentagon as demonstrated here.
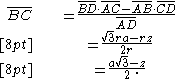
Based on his circle of diameter 200000 units and already established chords of pentagon, hexagon and triangle the calculation effected by Copernicus would have been:
A small rounding error is evident in the result but the corresponding entry (in the Copernican table of half chords ) of 10453 units against 6 degrees is correct as may readily be verified on a calculator (sin 6).
In modern trigonometric notation, the above calculation corresponds to the following application of a compound angle formula:
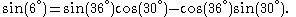
Compared with the previous we note that diameter BE has been swung across from point B to point E. EC and ED are joined. Since AEDB is a rectangle DE=AB. Thus in cyclic quadrilateral BEDC, sides BE, BC and ED are known along with diagonals CE and BD by application of the "Porism" (Pythagoras Thm). Then:
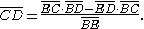
In the specific example illustrated in the diagram, calculation of chord CD in cyclic quadrilateral BEDC corresponds to the following application of a compound angle formula:
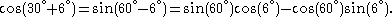
The required chord AC (in this example corresponding to sin(30+6)) is then calculated by application of the "Porism".
De Revolutionibus Orbium Coelestium: Liber Primus: Theorema Quintum
s inscribed in a circle with vertices P1, ..., Pn, if the sides are given together with all the length values of the "next to sides" chords connecting two vertices Pi and Pi+2
(with indices taken modulo
n).
Note that the proof is clearly only valid for simple cyclic quadrilaterals; if the quadrilateral is complex then K will be located outside the line segment AC, so AK−CK=±AC, giving the expected result.
Introducing polar coordinates one may represent the four vertices
in the form
After a possible renumbering of the Pi one can also assume that the four vertices appear in natural counterclockwise order which means that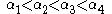
.
A basic result from trigonometry states that for two points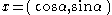
and 
on the unit circle written in polar coordinates their Euclidean distance
||x − y|| is given as
If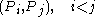
is an (ordered) pair of vertices of the given quadrilateral this formula implies
Ptolemy's relation
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
(a quadrilateral whose vertices lie on a common circle). The theorem is named after the Greek
Roman Greece
Roman Greece is the period of Greek history following the Roman victory over the Corinthians at the Battle of Corinth in 146 BC until the reestablishment of the city of Byzantium and the naming of the city by the Emperor Constantine as the capital of the Roman Empire...
astronomer
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
and mathematician
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
(Claudius Ptolemaeus). Ptolemy used the theorem as an aid to creating his table of chords
Ptolemy's table of chords
The table of chords, created by the astronomer and geometer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function...
, a trigonometric table that he applied to astronomy.
If the quadrilateral is given with its four vertices A, B, C, and D in order, then the theorem states that:
where the vertical lines denote the lengths of the line segments between the named vertices.
This relation may be verbally expressed as follows:
- If a quadrilateral is inscribable in a circle then the product of the measures of its diagonals is equal to the sum of the products of the measures of the pairs of opposite sides.
Moreover, the converse of Ptolemy's theorem is also true:
- In a quadrilateral, if the sum of the products of its two pairs of opposite sides is equal to the product of its diagonals, then the quadrilateral can be inscribed in a circle.
Equilateral triangle
Ptolemy's Theorem yields as a corollary a pretty theorem regarding an equilateral triangle inscribed in a circle.Given An equilateral triangle inscribed on a circle and a point on the circle.
The distance from the point to the most distant vertex of the triangle is the sum of the distances from the point to the two nearer vertices.
Proof: Follows immediately from Ptolemy's theorem:
Square
Any squareSquare (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
can be inscribed in a circle whose center is the barycenter of the square. If the common length of its four sides is equal to
then the length of the diagonal is equal to 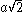according to the Pythagorean theoremPythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
and the relation obviously holds.
Rectangle
More generally, if the quadrilateral is a rectangleRectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
with sides a and b and diagonal d then Ptolemy's theorem reduces to the Pythagorean theorem. In this case the center of the circle coincides with the point of intersection of the diagonals. The product of the diagonals is then d2, the right hand side of Ptolemy's relation is the sum a2 + b2.
Copernicus − who used Ptolemy's theorem extensively in his trigonometrical work − refers to this result as a 'Porism' or self evident corollary:
- Furthermore it is clear (manifestum est) that when the chord subtending an arc has been given, that chord too can be found which subtends the rest of the semicircle.
De Revolutionibus Orbium Coelestium: Page 37. See last two lines of this page.
Nor for that matter does Copernicus refer to "Ptolemy's Theorem" but labels it more simply as "Theorema Secundum".
Pentagon
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
Side of decagon
If now diameter AF is drawn bisecting DC so that DF and CF are sides c of an inscribed decagon, Ptolemy's Theorem can again be applied – this time to cyclic quadrilateral ADFC with diameter d as one of its diagonals: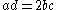 where is the golden ratio.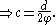whence the side of the inscribed decagon is obtained in terms of the circle diameter. Pythagoras' Theorem applied to right triangle AFD then yields "b" in terms of the diameter and "a" the side of the pentagon is thereafter calculated as
As Copernicus (following Ptolemy) wrote,
- "The diameter of a circle being given, the sides of the triangle, tetragon, pentagon, hexagon and decagon, which the same circle circumscribes, are also given." – De Revolutionibus Orbium Coelestium: Liber Primus: Theorema Primum
Complement of pentagon chord
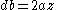
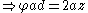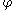The ancient geometers are not done yet, for if the fifth vertex of the pentagon is marked as E and FE and BF are joined (with FE=BF=z), then cyclic quadrilateral EFBA will be formed with diagonals length d (diameter) and b. Applying the 'Almagest' theorem yet again: where is the golden ratio.z subtends 540 at the circumference, c (the side of the decagon) subtends 180 at the circumference and thereby is established:
and 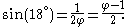And since angle ABF is subtended by the diameter and is therefore right, the side of the pentagon is calculated by an even simpler route:
Based on his circle of diameter 200000 units, Copernicus provides accurate numerical values for the four pentagon related chords corresponding to these angles:
- "Since the side of the decagon which subtends 360 has been shown to have 61803 parts, whereof the diameter has 200000 parts – the chord which subtends the remaining 1440 of the semicircle has 190211 parts. And in the case of side of the pentagon, which is equal to 117557 parts of the diameter and subtends an arc of 720, a straight line of 161803 parts is given, and it subtends the remaining 1080 of the circle".
Golden ratio aficionados will instantly recognize the digits 161803 and 61803 as corresponding to
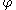and its reciprocal. The chords are of considerable historical importance because, along with the sides of the triangle and tetragon (square), they enable the generation of a table of half chords (effectively sine values) which in turn underpins many of the key astronomical measurements and calculations effected by Copernicus in the development of his helio-centric model:- "Because the proofs which we shall use in almost the entire work deal with straight lines and arcs, with plane and spherical triangles and because Euclid's Elements, although they clear up much of this, do not have what is here most required, namely, how to find the sides from angles and the angles from the sides ... there has accordingly been found a method whereby the lines subtending any arc may be known."
Euclid 13:10
Next our attention is drawn to point G midway between points B and C on the circumference. CG, FG and DG are joined forming cyclic quadrilateral DFCG in which three sides belong to the regular decagon (length c) and the fourth DG is of length z. Diagonals DC and FG are both of length a (side of the pentagon) Then:Therefore
where r is the radius of the circle and also the side of the inscribed hexagon.
Whence with relative ease is proved Proposition 10 in Book XIII of Euclid's Elements: The square on the side of the pentagon equals the sum of the squares on the sides of the hexagon and the decagon inscribed in the same circle.
In modern trigonometric notation this corresponds to the identity:
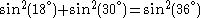
The Pythagorean nature of this relationship makes possible the construction of a regular pentagon as demonstrated here.
Theorema Tertium
A well documented classical application of the "Second Theorem" as illustrated in the diagram is the determination of chord BC subtending 12 degrees of arc. Referring to the diagram: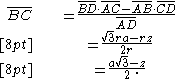- "When, for example, the sides of the pentagon and hexagon are given from the above, by this computation a line is given subtending 120 which is the difference between the arcs − and it is equal to 20905 parts of the diameter." De Revolutionibus Orbium Coelestium: Liber Primus: Theorema Tertium
Based on his circle of diameter 200000 units and already established chords of pentagon, hexagon and triangle the calculation effected by Copernicus would have been:
A small rounding error is evident in the result but the corresponding entry (in the Copernican table of half chords ) of 10453 units against 6 degrees is correct as may readily be verified on a calculator (sin 6).
In modern trigonometric notation, the above calculation corresponds to the following application of a compound angle formula:
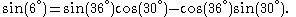
Theorema Quintum
The previous diagram demonstrated a general technique for calculating the chord subtending the difference between two arcs. The following diagram neatly reverses this procedure to obtain the chord subtending the sum of arcs: ie determination of chord AC given chords AB and BC.Compared with the previous we note that diameter BE has been swung across from point B to point E. EC and ED are joined. Since AEDB is a rectangle DE=AB. Thus in cyclic quadrilateral BEDC, sides BE, BC and ED are known along with diagonals CE and BD by application of the "Porism" (Pythagoras Thm). Then:
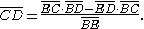
In the specific example illustrated in the diagram, calculation of chord CD in cyclic quadrilateral BEDC corresponds to the following application of a compound angle formula:
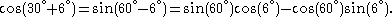
The required chord AC (in this example corresponding to sin(30+6)) is then calculated by application of the "Porism".
De Revolutionibus Orbium Coelestium: Liber Primus: Theorema Quintum
Other polygons
When applied repeatedly, Ptolemy's theorem allows one to compute the lengths of all diagonals for polygonPolygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s inscribed in a circle with vertices P1, ..., Pn, if the sides are given together with all the length values of the "next to sides" chords connecting two vertices Pi and Pi+2
(with indices taken modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
n).
Geometric proof
- Let ABCD be a cyclic quadrilateralCyclic quadrilateralIn Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
. - Note that on the chordChord (geometry)A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
BC, the inscribed angleInscribed angleIn geometry, an inscribed angle is formed when two secant lines of a circle intersect on the circle....
s ∠BAC = ∠BDC, and on AB, ∠ADB = ∠ACB. - Construct K on AC such that ∠ABK = ∠CBD;
- Note that since ∠ABK + ∠CBK = ∠ABC = ∠CBD + ∠ABD, ∠CBK = ∠ABD.
- Now, by common angles △ABK is similarSimilarity (geometry)Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
to △DBC, and likewise △ABD ∼ △KBC. - Thus AK/AB = CD/BD, and CK/BC = DA/BD;
- Thus AK·BD = AB·CD, and CK·BD = BC·DA;
- By adding equality: AK·BD + CK·BD = AB·CD + BC·DA;
- Thus by factorizing: (AK+CK)·BD = AB·CD + BC·DA;
- But AK+CK = AC, so AC·BD = AB·CD + BC·DA; Q.E.D.Q.E.D.Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
Note that the proof is clearly only valid for simple cyclic quadrilaterals; if the quadrilateral is complex then K will be located outside the line segment AC, so AK−CK=±AC, giving the expected result.
Trigonometric proof
It suffices to prove the theorem for the standard unit circle (the statement of the theorem is invariant under re-scaling and translation).Introducing polar coordinates one may represent the four vertices
in the form
After a possible renumbering of the Pi one can also assume that the four vertices appear in natural counterclockwise order which means that
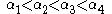.A basic result from trigonometry states that for two points
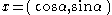and on the unit circle written in polar coordinates their Euclidean distanceDistance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
||x − y|| is given as
If
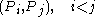is an (ordered) pair of vertices of the given quadrilateral this formula implies
Ptolemy's relation
-
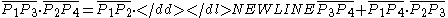
then follows from the quadratic addition relation
satisfied by the sineSineIn mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
-function which in turn can be deduced from the trigonometric identity (which is the products-to-sum identity for the sineSineIn mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
)
applied to each of the three products of sines (the resulting six terms cancel out in pairs).
Concluding remark (explaining the naming "addition relation"):
If one introduces the difference angles
for 
then the relation
turns into
Solving for
, this relation may be interpreted as a "triple" addition relation expressing the sine of a triple angle sum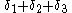 
as a rational expression in the sine values 
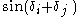and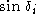 
.
Written out explicitly:
Proof using the law of sines
The proof which follows is substantively similar to the previous but adopts a different methodology and concludes with an interestingly symmetric formula for the product of diagonals and sum of products of opposite sides.
Preliminary observations and identities
In the diagram sides AB,BC,CD and DA are labelled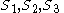
and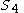 
and subtend angles 
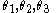and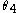 
respectively. Applying sum of angles in triangle ABC it should be noted that 
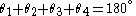. Therefore the sum of any two angles is supplementary with the sum of the other two and any single angle is supplementary with the sum of the other three. In general for supplementary angles x and y:
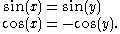
We will also need the identity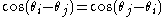
and the following product to sum identity:
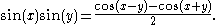
Proof
Apply the sine rule to triangles ABC, ADC and ABD within their common circumscribing circle ABCD with radius R:
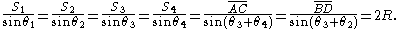
From this we obtain:
The product to sum identity has been applied twice and the middle two terms cancel out on account of being cosines of supplementary angles.
Similarly we can obtain an expression for the product of diagonals:
Once again the product to sum identity has been applied and the second term has been rewritten in terms of its supplementary angle.
We may now present Ptolemy's theorem with an addendum by way of the "marrying formula" for product of diagonals and sum of products of opposite sides:
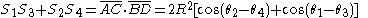
where R is the radius of the circumscribing circle and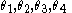
are the angles subtended by sides 
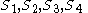respectively.
In the case of a circle of unit diameter, Ptolemy's theorem can be written in trigonometric form as follows:
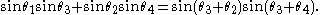
Algebraic proof
An alternative proof can be given using complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
calculus and projective analytic geometryAnalytic geometryAnalytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, introducing complex coordinates for the vertices of the quadrilateral. Again it suffices to prove the theorem for the standard unit circle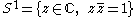
.
Ptolemy's Relation
can be reformulated as
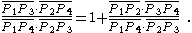
Written in this form Ptolemy's theorem is in fact a "disguised" form of the relation
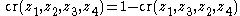
valid for the cross-ratioCross-ratioIn geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
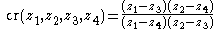of any four (pairwise different) complex numbers 
.
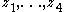To make this connection explicit one represents the four vertices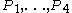
as four complex numbers 
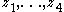of norm one, arranged in (counterclockwise) cyclic order on the unit circle. For two complex numbers 
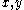on the unit circle their squared distance
equals
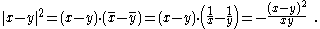
Therefore for any quadruple of (pairwise different) complex numbers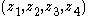
on the unit circle the square of the "length cross-ratio"
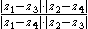
is equal to the square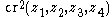
of the ordinary ("complex points" ) cross-ratio 
.
Taking square roots one first deduces
for any quadruple
of points on the unit circle. The sign factor 
depends on the relative position of the four points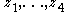 
on the unit circle and can be determined using the invariance of the cross-ratio under a linear fractional transformation 
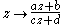. Assume that the quadruple 
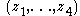on the unit circle is arranged in natural (counterclockwise) cyclic order. Then
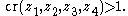
This property can be proved using the projective transformation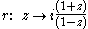
(which is the "inverse Cayley transformCayley transformIn mathematics, the Cayley transform, named after Arthur Cayley, has a cluster of related meanings. As originally described by , the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. In complex analysis, the Cayley transform is a conformal mapping in...
"). It maps
the punctured unit circle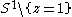
(continuously) to the real line 
(with the upper (resp. lower) arc of the unit circle mapping to the negative (resp. positive) half-line). In polar coordinates the map is given as 
which shows that it defines a monotone function in the "angle" coordinate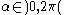 
. Therefore the sign of the cross-ratio can be read off from the mutual order of the image points on the real line. After multiplying the 
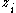with a suitable scalar 
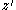of norm 1 one may in addition assume that 
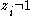for all 
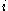. If the quadruple 
on the unit circle (punctured at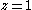 
) is arranged in natural (counterclockwise) cyclic order the image quadruple 
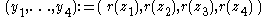satisfies 
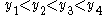. The relation
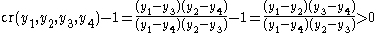
then shows that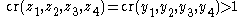
. On the other hand, if one interchanges the middle pair 
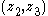in a cyclically ordered quadruple then the cross-ratio will become negative because
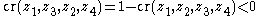, using the relation of cross-ratios
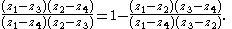
Summarizing the sign discussion one obtains that for a quadruple
of (pairwise different) points on the unit circle given in (counterclockwise) cyclic order one has
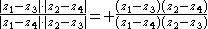
and
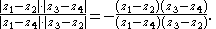
Ptolemy's relation
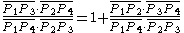
can now be interpreted as the algebraic relation (already used above) between cross-ratioCross-ratioIn geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
s
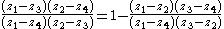
using the representation of the vertices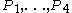
as the points 
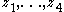on the unit circle.
Corollaries
In the case of a circle of unit diameter the sides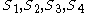
of any cyclic quadrilateral ABCD are numerically equal to the sines of the angles 
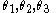and 
which they subtend. Similarly the diagonals are equal to the sine of the sum of whichever pair of angles they subtend. We may then write Ptolemy's Theorem in the following trigonometric form:
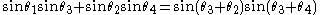
Applying certain conditions to the subtended angles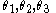
and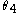 
it is possible to derive a number of important corollaries using the above as our starting point. In what follows it is important to bear in mind that the sum of angles 
.
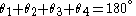Corollary 1. Pythagoras' theorem
Let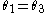
and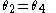 
. Then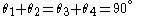 
(since opposite angles of a cyclic quadrilateral are supplementary). Then:
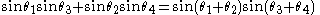
Corollary 2. The law of cosines
Let
. The rectangle of corollary 1 is now a symmetrical trapezium with equal diagonals and a pair of equal sides. The parallel sides differ in length by 2x units where:
It will be easier in this case to revert to the standard statement of Ptolemy's theorem:
The cosine rule for triangle ABC.
Corollary 3: Compound angle sine (+)
Let
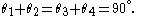
Then
Therefore
Formula for compound angle sine (+).
Corollary 4: Compound angle sine (−)
Let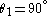
. Then 
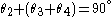. Hence,
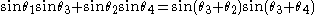
Formula for compound angle sine (−).
This derivation corresponds to the Third Theorem
as chronicled by Copernicus following PtolemyPtolemyClaudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
in AlmagestAlmagestThe Almagest is a 2nd-century mathematical and astronomical treatise on the apparent motions of the stars and planetary paths. Written in Greek by Claudius Ptolemy, a Roman era scholar of Egypt,...
. In particular if the sides of a pentagon (subtending 36° at the circumference) and of a hexagon (subtending 30° at the circumference) are given, a chord subtending 6° may be calculated. This was a critical step in the ancient method of calculating tables of chords.
Corollary 5: Compound angle cosine (+)
This corollary is the core of the Fifth Theorem as chronicled by Copernicus following Ptolemy in Almagest.
Let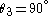
. Then 
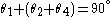. Hence
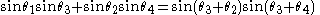
Formula for compound angle cosine (+)
Despite lacking the dexterity of our modern trigonometric notation, it should be clear from the above corollaries that in Ptolemy's theorem (or more simply the Second Theorem) the ancient world had at its disposal an extremely flexible and powerful trigonometric tool which enabled the cognoscenti of those times to draw up accurate tables of chords (corresponding to tables of sines) and to use these in their attempts to understand and map the cosmos as they saw it. Since tables of chords were drawn up by HipparchusHipparchusHipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
three centuries before Ptolemy, we must assume he knew of the 'Second Theorem' and its derivatives. Following the trail of ancient astronomers, history records the star catalogue of TimocharisTimocharisTimocharis of Alexandria was a Greek astronomer and philosopher. Likely born in Alexandria, he was a contemporary of Euclid....
of Alexandria. If, as seems likely, the compilation of such catalogues required an understanding of the 'Second Theorem' then the true origins of the latter disappear thereafter into the mists of antiquity but it cannot be unreasonable to presume that the astronomers, architects and construction engineers of ancient Egypt may have had some knowledge of it.
Ptolemy's inequality
The equation in Ptolemy's theorem is never true with non-cyclic quadrilaterals. Ptolemy's inequality is an extension of this fact, and it is a more general form of Ptolemy's theorem. It states that, given a quadrilateral ABCD, then
where equality holds if and only if the quadrilateral is cyclicCyclic quadrilateralIn Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
. This special case is equivalent to Ptolemy's theorem.
External links
- Proof of Ptolemy's Theorem for Cyclic Quadrilateral
- MathPages − On Ptolemy's Theorem
- Ptolemy's Theorem at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Compound angle proof at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Ptolemy's Theorem on PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
- Ptolemy Inequality on MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
- De Revolutionibus Orbium Coelestium at Harvard.
- Deep Secrets: The Great Pyramid, the Golden Ratio and the Royal Cubit
- Ptolemy's Theorem by Jay Warendorff, The Wolfram Demonstrations Project.
- Book XIII of Euclid's Elements
-
