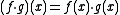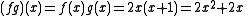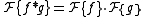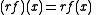Pointwise product
Encyclopedia
The pointwise product of two function
s is another function, obtained by multiplying the image of the two functions at each value in the domain. If f and g are both functions with domain
X and codomain
Y, and elements of Y can be multiplied (for instance, Y could be some set of numbers), then the pointwise product of f and g is another function from X to Y which maps x ∈ X to f(x)g(x).
be defined in Y—that is, for each y and z in Y let the product
be well-defined. Let f and g be function
s f, g : X → Y. Then the pointwise product (f • g) : X → Y is defined by
for each x in X. In the same manner in which the binary operator • is omitted from products, we say that f • g = fg.
(or field
), in which multiplication is well-defined.
for every real number x in R.
. Since addition
and multiplication
are defined in R, we can construct an algebraic structure known as an algebra out of the functions from X to R by defining addition, multiplication, and scalar multiplication of functions to be done pointwise.
If R X denotes the set of functions from X to R, then we say that if f, g are elements of R X, then f + g, fg, and rf, the last of which is defined by
for all r in R, are all elements of R X.
of both sets. The value of each assignment is calculated as the product of the values of both functions given to each one the subset of the assignment that is in its domain.
For example, given the function f1 for the boolean variables p and q, and f2 for the boolean variables q and r, both with the range
in R, the pointwise product of f1 and f2 is shown in the next table:
{| border=1 cellspacing=0 cellpadding=5
|- style="background:silver"
| p || q || r || f1(p, q) || f2(q, r) || pointwise product
|- align="center"
| T || T || T || 0.1 || 0.2 || 0.1 x 0.2
|- align="center"
| T || T || F || 0.1 || 0.4 || 0.1 x 0.4
|- align="center"
| T || F || T || 0.3 || 0.6 || 0.3 x 0.6
|- align="center"
| T || F || F || 0.3 || 0.8 || 0.3 x 0.8
|- align="center"
| F || T || T || 0.5 || 0.2 || 0.5 x 0.2
|- align="center"
| F || T || F || 0.5 || 0.4 || 0.5 x 0.4
|- align="center"
| F || F || T || 0.7 || 0.6 || 0.7 x 0.6
|- align="center"
| F || F || F || 0.7 || 0.8 || 0.7 x 0.8
|}
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s is another function, obtained by multiplying the image of the two functions at each value in the domain. If f and g are both functions with domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
X and codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
Y, and elements of Y can be multiplied (for instance, Y could be some set of numbers), then the pointwise product of f and g is another function from X to Y which maps x ∈ X to f(x)g(x).
Formal definition
Let X and Y be sets, and let multiplicationMultiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
be defined in Y—that is, for each y and z in Y let the product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
-
 given by
given by 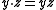
be well-defined. Let f and g be function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s f, g : X → Y. Then the pointwise product (f • g) : X → Y is defined by
for each x in X. In the same manner in which the binary operator • is omitted from products, we say that f • g = fg.
Examples
The most common case of the pointwise product of two functions is when the co-domain is a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
(or field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
), in which multiplication is well-defined.
- If Y is the set of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R, then the pointwise product of f, g : X → R is just normal multiplication of the images. For example, if we have f(x) = 2x and g(x) = x + 1 then
for every real number x in R.
- The convolution theoremConvolution theoremIn mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
states that the Fourier transform of a convolution is the pointwise product of Fourier transforms:
Algebraic application of pointwise products
Let X be a set and let R be a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. Since addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
are defined in R, we can construct an algebraic structure known as an algebra out of the functions from X to R by defining addition, multiplication, and scalar multiplication of functions to be done pointwise.
If R X denotes the set of functions from X to R, then we say that if f, g are elements of R X, then f + g, fg, and rf, the last of which is defined by
for all r in R, are all elements of R X.
Generalization
If both f and g have as their domain all possible assignments of a set of discrete variables, then their pointwise product is a function whose domain is constructed by all possible assignments of the unionUnion (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of both sets. The value of each assignment is calculated as the product of the values of both functions given to each one the subset of the assignment that is in its domain.
For example, given the function f1 for the boolean variables p and q, and f2 for the boolean variables q and r, both with the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
in R, the pointwise product of f1 and f2 is shown in the next table:
{| border=1 cellspacing=0 cellpadding=5
|- style="background:silver"
| p || q || r || f1(p, q) || f2(q, r) || pointwise product
|- align="center"
| T || T || T || 0.1 || 0.2 || 0.1 x 0.2
|- align="center"
| T || T || F || 0.1 || 0.4 || 0.1 x 0.4
|- align="center"
| T || F || T || 0.3 || 0.6 || 0.3 x 0.6
|- align="center"
| T || F || F || 0.3 || 0.8 || 0.3 x 0.8
|- align="center"
| F || T || T || 0.5 || 0.2 || 0.5 x 0.2
|- align="center"
| F || T || F || 0.5 || 0.4 || 0.5 x 0.4
|- align="center"
| F || F || T || 0.7 || 0.6 || 0.7 x 0.6
|- align="center"
| F || F || F || 0.7 || 0.8 || 0.7 x 0.8
|}