
Planck's law of black body radiation
Encyclopedia

Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Planck's law describes the amount of energy emitted by a black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
in radiation of a certain wavelength (i.e. the spectral radiance of a black body). The law is named after Max Planck
Max Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
, who originally proposed it in 1900. The law was the first to accurately describe black body radiation, and resolved the ultraviolet catastrophe
Ultraviolet catastrophe
The ultraviolet catastrophe, also called the Rayleigh–Jeans catastrophe, was a prediction of late 19th century/early 20th century classical physics that an ideal black body at thermal equilibrium will emit radiation with infinite power....
. It is a pioneer result of modern physics
Modern physics
The term modern physics refers to the post-Newtonian conception of physics. The term implies that classical descriptions of phenomena are lacking, and that an accurate, "modern", description of reality requires theories to incorporate elements of quantum mechanics or Einsteinian relativity, or both...
and quantum theory
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
In terms of frequency (
 ) or wavelength (λ), Planck's law is written:
) or wavelength (λ), Planck's law is written: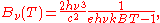

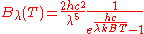
where B is the spectral radiance, T is the absolute temperature of the black body, kB is the Boltzmann constant, h is the Planck constant
Planck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
, and c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. However these are not the only ways to express the law; expressing it in terms of wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
rather than frequency or wavelength is also common, as are expression in terms of the number of photons emitted at a certain wavelength, rather than energy emitted. In the limit of low frequencies (i.e. long wavelengths), Planck's law becomes the Rayleigh–Jeans law, while in the limit of high frequencies (i.e. small wavelengths) it tends to the Wien approximation.
Max Planck
Max Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
developed the law in 1900, originally with only empirically determined constants, and later showed that, expressed as an energy distribution, it is the unique stable distribution for radiation in thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
. As an energy distribution, it is one of a family of thermal equilibrium distributions which include the Bose–Einstein distribution, the Fermi–Dirac distribution and the Maxwell–Boltzmann distribution.
Different forms
Planck's law can be encountered in several forms depending on the conventions and preferences of different scientific fields. The various forms of the law for spectral radiance are summarized in the table below. Forms on the left are most often encountered in experimental fieldsExperimental physics
Within the field of physics, experimental physics is the category of disciplines and sub-disciplines concerned with the observation of physical phenomena in order to gather data about the universe...
, while those on the right are most often encountered in theoretical fields
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
.
| with h | with ħ | ||
|---|---|---|---|
| variable | distribution | variable | distribution |
| Frequency Frequency Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...  |
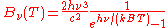 |
Angular frequency Angular frequency In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...  |
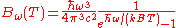 |
| Wavelength Wavelength In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a... 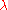 |
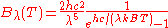 |
Angular wavelength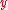 |
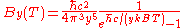 |
| Wavenumber Wavenumber In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...  |
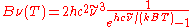 |
Angular wavenumber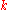 |
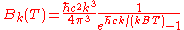 |
These distributions represent the spectral radiance of blackbodies—the power emitted from the emitting surface, per unit projected area of emitting surface, per unit solid angle
Solid angle
The solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point...
, per spectral unit (frequency, wavelength, wavenumber or their angular equivalents). Since the radiance is isotropic (i.e. independent of direction), the power emitted at an angle to the normal is proportional to the projected area, and therefore to the cosine of that angle as per Lambert's cosine law
Lambert's cosine law
In optics, Lambert's cosine law says that the radiant intensity observed from a Lambertian surface or a Lambertian radiator is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal. A Lambertian surface is also known as an ideal diffusely...
, and is unpolarized.
The relation between the spectral radiance expressed in terms of two different variables i and j with a one-to-one
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
relationship (frequency and wavelength, for example) is given by the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
of calculus, with the added assumption that the energy from any bandwidth is a positive number:
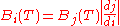
This means that the energy from an infinitesimal bandwidth di is equal to the energy from the corresponding infinitesimal bandwidth dj. This has two main implications. The first is that, in general, one may not convert between the various forms of Planck's law simply by substituting one variable for another. The second that the peak of the distributions depends on which variable is chosen for the expression of Planck's law.
Planck's law can also be written in terms of the spectral energy density
Energy density
Energy density is a term used for the amount of energy stored in a given system or region of space per unit volume. Often only the useful or extractable energy is quantified, which is to say that chemically inaccessible energy such as rest mass energy is ignored...
(u) by multiplying B by 4π/c:
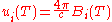
These distributions have units of energy per volume per spectral unit.
Peaks
The distributions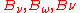 and
and  peak at
peak at
where W is the Lambert W function.
The distributions
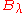 and
and 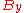 however, peak at a different energy
however, peak at a different energy
The reason for this is that, as mentioned above, one cannot go from (for example)
 to
to 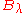 simply by substituting
simply by substituting  by
by  . In addition, one must also multiply the result of the substitution by
. In addition, one must also multiply the result of the substitution by 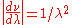 . This
. This 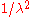 factor shifts the peak of the distribution to higher energies.
factor shifts the peak of the distribution to higher energies.Approximations
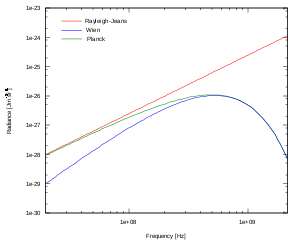
In the limit of low frequencies (i.e. long wavelengths), Planck's law becomes the Rayleigh–Jeans law
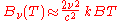 or
or 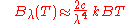
The radiance increases as the square of the frequency, illustrating the ultraviolet catastrophe
Ultraviolet catastrophe
The ultraviolet catastrophe, also called the Rayleigh–Jeans catastrophe, was a prediction of late 19th century/early 20th century classical physics that an ideal black body at thermal equilibrium will emit radiation with infinite power....
. In the limit of high frequencies (i.e. small wavelengths) Planck's law tends to the Wien approximation:
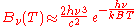 or
or 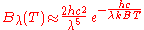
Both approximations were known to Planck before he developed his law. He was led by these two approximations to develop a law which incorporated both limits, which ultimately became Planck's law.
Percentiles
Wien's displacement law
Wien's displacement law states that the wavelength distribution of thermal radiation from a black body at any temperature has essentially the same shape as the distribution at any other temperature, except that each wavelength is displaced on the graph...
in its stronger form states that the shape of Planck's law is independent of temperature. It is therefore possible to list the percentile points of the total radiation as well as the peaks for wavelength and frequency, in a form which gives the wavelength λ when divided by temperature T. The second row of the following table lists the corresponding values of λT, that is, those values of x for which the wavelength λ is x/T micrometers at the radiance percentile point given by the corresponding entry in the first row.
| Percentile | 0.01% | 0.1% | 1% | 10% | 20% | 25.0% | 30% | 40% | 41.8% | 50% | 60% | 64.6% | 70% | 80% | 90% | 99% | 99.9% | 99.99% |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λT (μm·K) | 910 | 1110 | 1448 | 2195 | 2676 | 2898 | 3119 | 3582 | 3670 | 4107 | 4745 | 5099 | 5590 | 6864 | 9376 | 22884 | 51613 | 113374 |
That is, 0.01% of the radiation is at a wavelength below 910/T µm, 20% below 2676/T µm, etc. The wavelength and frequency peaks are in bold and occur at 25.0% and 64.6% respectively. The 41.8% point is the wavelength-frequency-neutral peak. These are the points at which the respective Planck-law functions 1/λ5,
 , and
, and 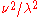 divided by attain their maxima. Also note the much smaller gap in ratio of wavelengths between 0.1% and 0.01% (1110 is 22% more than 910) than between 99.9% and 99.99% (113374 is 120% more than 51613), reflecting the exponential decay of energy at short wavelengths (left end) and polynomial decay at long.
divided by attain their maxima. Also note the much smaller gap in ratio of wavelengths between 0.1% and 0.01% (1110 is 22% more than 910) than between 99.9% and 99.99% (113374 is 120% more than 51613), reflecting the exponential decay of energy at short wavelengths (left end) and polynomial decay at long.Which peak to use depends on the application. The conventional choice is the wavelength peak at 25.0% given by Wien's displacement law
Wien's displacement law
Wien's displacement law states that the wavelength distribution of thermal radiation from a black body at any temperature has essentially the same shape as the distribution at any other temperature, except that each wavelength is displaced on the graph...
in its weak form. For some purposes the median or 50% point dividing the total radiation into two halves may be more suitable. The latter is closer to the frequency peak than to the wavelength peak because the radiance drops exponentially at short wavelengths and only polynomially at long. The neutral peak occurs at a shorter wavelength than the median for the same reason.
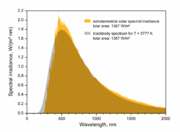
For the Sun, T is 5778 K, allowing the percentile points of the Sun's radiation, in nanometers, to be tabulated as follows when modeled as a black body radiator, to which the Sun is a fair approximation. For comparison a planet modeled as a black body radiating at a nominal 288 K (15 °C) as a representative value of the Earth's highly variable temperature has wavelengths more than twenty times that of the Sun, tabulated in the third row in micrometers (thousands of nanometers).
| Percentile | 0.01% | 0.1% | 1% | 10% | 20% | 25.0% | 30% | 40% | 41.8% | 50% | 60% | 64.6% | 70% | 80% | 90% | 99% | 99.9% | 99.99% |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sun λ (nm) | 157 | 192 | 251 | 380 | 463 | 502 | 540 | 620 | 635 | 711 | 821 | 882 | 967 | 1188 | 1623 | 3961 | 8933 | 19620 |
| 288 K planet λ (µm) | 3.16 | 3.85 | 5.03 | 7.62 | 9.29 | 10.1 | 10.8 | 12.4 | 12.7 | 14.3 | 16.5 | 17.7 | 19.4 | 23.8 | 32.6 | 79.5 | 179 | 394 |
That is, only 1% of the Sun's radiation is at wavelengths shorter than 251 nm, and only 1% at longer than 3961 nm. Expressed in micrometers this puts 98% of the Sun's radiation in the range from 0.251 to 3.961 µm. The corresponding 98% of energy radiated from a 288 K planet is from 5.03 to 79.5 µm, well above the range of solar radiation (or below if expressed in terms of frequencies
 instead of wavelengths λ).
instead of wavelengths λ).A consequence of this more-than-order-of-magnitude difference in wavelength between solar and planetary radiation is that filters designed to pass one and block the other are easy to construct. For example windows fabricated of ordinary glass or transparent plastic pass at least 80% of the incoming 5778 K solar radiation, which is below 1.2 µm in wavelength, while blocking over 99% of the outgoing 288 K thermal radiation from 5 µm upwards, wavelengths at which most kinds of glass and plastic of construction-grade thickness are effectively opaque.
The Sun's radiation is that arriving at the top of the atmosphere (TOA). As can be read from the table, radiation below 400 nm, or ultraviolet
Ultraviolet
Ultraviolet light is electromagnetic radiation with a wavelength shorter than that of visible light, but longer than X-rays, in the range 10 nm to 400 nm, and energies from 3 eV to 124 eV...
, is about 12%, while that above 700 nm, or infrared
Infrared
Infrared light is electromagnetic radiation with a wavelength longer than that of visible light, measured from the nominal edge of visible red light at 0.74 micrometres , and extending conventionally to 300 µm...
, starts at about the 49% point and so accounts for 51% of the total. Hence only 37% of the TOA insolation is visible to the human eye. The atmosphere shifts these percentages substantially in favor of visible light as it absorbs most of the ultraviolet and significant amounts of infrared.
Derivation
- The following derivation of Planck's law can be found in .
Consider a cube of side L with conducting walls filled with electromagnetic radiation. Let the cube contain a small particle of black material such as black carbon, so that the radiation will be transduced to black radiation in thermodynamic equilibrium. Planck noted that such a transducer between frequency components is needed because without it the free electromagnetic field in the cavity with perfectly conducting walls cannot exchange energy between frequency components and cannot achieve stable thermodynamic equilibrium. If there is a small hole in one of the walls, the radiation emitted from the hole will be characteristic of a perfect black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
. We will first calculate the spectral energy density within the cavity and then determine the spectral radiance of the emitted radiation.
At the walls of the cube, the parallel component of the electric field and the orthogonal component of the magnetic field must vanish. Analogous to the wave function of a particle in a box
Particle in a box
In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
, one finds that the fields are superpositions of periodic functions. The three wavelengths λ1, λ2, and λ3, in the three directions orthogonal to the walls can be:
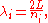
where the ni are integers. For each set of integers ni there are two linear independent solutions (modes). According to quantum theory, the energy levels of a mode are given by:
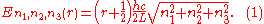
The quantum number r can be interpreted as the number of photons in the mode. The two modes for each set of ni correspond to the two polarization states of the photon which has a spin of 1. Note that for the energy of the mode is not zero. This vacuum energy of the electromagnetic field is responsible for the Casimir effect
Casimir effect
In quantum field theory, the Casimir effect and the Casimir–Polder force are physical forces arising from a quantized field. The typical example is of two uncharged metallic plates in a vacuum, like capacitors placed a few micrometers apart, without any external electromagnetic field...
. In the following we will calculate the internal energy of the box at temperature T relative to the vacuum energy.
According to statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the probability distribution over the energy levels of a particular mode is given by:

Here
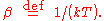
The denominator Z(β), is the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
of a single mode and makes Pr properly normalized:
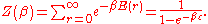
Here we have implicitly defined
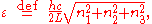
which is the energy of a single photon. As explained here, the average energy in a mode can be expressed in terms of the partition function:
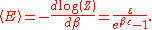
This formula is a special case of the general formula for particles obeying Bose–Einstein statistics
Bose–Einstein statistics
In statistical mechanics, Bose–Einstein statistics determines the statistical distribution of identical indistinguishable bosons over the energy states in thermal equilibrium.-Concept:...
. Since there is no restriction on the total number of photons, the chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
is zero.
The total energy in the box now follows by summing
 over all allowed single photon states. This can be done exactly in the thermodynamic limit as L approaches infinity. In this limit, ε becomes continuous and we can then integrate
over all allowed single photon states. This can be done exactly in the thermodynamic limit as L approaches infinity. In this limit, ε becomes continuous and we can then integrate  over this parameter. To calculate the energy in the box in this way, we need to evaluate how many photon states there are in a given energy range. If we write the total number of single photon states with energies between ε and ε + dε as g(ε)dε, where g(ε) is the density of states
over this parameter. To calculate the energy in the box in this way, we need to evaluate how many photon states there are in a given energy range. If we write the total number of single photon states with energies between ε and ε + dε as g(ε)dε, where g(ε) is the density of statesDensity of states
In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...
which we'll evaluate in a moment, then we can write:
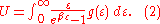
To calculate the density of states we rewrite equation (1) as follows:
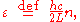
where n is the norm of the vector :

For every vector n with integer components larger than or equal to zero, there are two photon states. This means that the number of photon states in a certain region of n-space is twice the volume of that region. An energy range of dε corresponds to shell of thickness dn = (2L/hc)dε in n-space. Because the components of n have to be positive, this shell spans an octant of a sphere. The number of photon states g(ε)dε, in an energy range dε, is thus given by:

Inserting this in Eq. (2) gives:

From this equation one easily derives the spectral energy density as a function of frequency
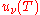 and as a function of wavelength uλ(T):
and as a function of wavelength uλ(T):
where:
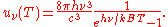
And:
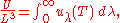
where

This is also a spectral energy density function with units of energy per unit wavelength per unit volume. Integrals of this type for Bose and Fermi gases can be expressed in terms of polylogarithms. In this case, however, it is possible to calculate the integral in closed form using only elementary functions. Substituting
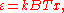
in Eq. (3), makes the integration variable dimensionless giving:
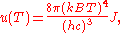
where J is a Bose–Einstein integral given by:
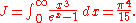
The total electromagnetic energy inside the box is thus given by:
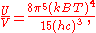
where V = L3 is the volume of the box.
This is not the Stefan–Boltzmann law (which provides the total energy radiated by a black body per unit surface area per unit time), but it can be written more compactly using the Stefan–Boltzmann constant σ, giving
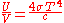
The constant 4σ/c is sometimes called the radiation constant.
Since the radiation is the same in all directions, and propagates at the speed of light (c), the spectral radiance of radiation exiting the small hole is

which yields
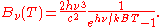
It can be converted to an expression for Bλ(T) in wavelength units by substituting
 by c/λ and evaluating
by c/λ and evaluating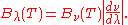
Note that dimensional analysis shows that the unit of steradians, shown in the denominator of left hand side of the equation above, is generated in and carried through the derivation but does not appear in any of the dimensions for any element on the left-hand-side of the equation.
Physics
The essential nature of black body (or Planckian) radiation is that it is the radiation resulting from thermal equilibrium. Thermal equilibrium is characterized by the absence of any net flow of energy. Just as a material body is characterized by a particular temperature and energy distribution (e.g. the Boltzmann distributionBoltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
) when it is in thermal equilibrium, so too, the electromagnetic field may be thought of as a photon gas
Photon gas
In physics, a photon gas is a gas-like collection of photons, which has many of the same properties of a conventional gas like hydrogen or neon - including pressure, temperature, and entropy...
, characterized by a particular temperature and energy distribution (expressed by Planck's law) when it is in thermal equilibrium.
Kirchhoff's law
If there is a material body in thermal equilibriumThermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
with the radiation field, then the radiation power falling upon a small area element of that body must be equal to the amount of radiation power leaving that element. There are two ways that radiation may leave such an area element – reflection or scattering and emission. This assumes that the material body is large enough to be opaque – there is no radiation leaving the element that has been transmitted through the body. At a particular frequency, the power directed into the area element at equilibrium will be equal to the equilibrium distribution
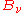 (without necessarily specifying what that distribution is). Defining
(without necessarily specifying what that distribution is). Defining  as the fraction of incident radiation absorbed at the surface, the rate at which this energy is absorbed will be
as the fraction of incident radiation absorbed at the surface, the rate at which this energy is absorbed will be 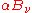 . By conservation of energy, the rest must be reflected or scattered, which will be proportional to
. By conservation of energy, the rest must be reflected or scattered, which will be proportional to 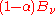 . The area element will also emit its own thermal radiation which may be expressed as a proportion of the equilibrium radiation:
. The area element will also emit its own thermal radiation which may be expressed as a proportion of the equilibrium radiation: 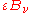 , where
, where  is the emissivity
is the emissivityEmissivity
The emissivity of a material is the relative ability of its surface to emit energy by radiation. It is the ratio of energy radiated by a particular material to energy radiated by a black body at the same temperature...
of the surface. Since, at equilibrium, the rate of energy arriving must equal the rate leaving, it follows that:

or, equivalently
 , which is just Kirchhoff's law
, which is just Kirchhoff's lawKirchhoff's law of thermal radiation
In thermodynamics, Kirchhoff's law of thermal radiation, or Kirchhoff's law for short, is a general statement equating emission and absorption in heated objects, proposed by Gustav Kirchhoff in 1859, following from general considerations of thermodynamic equilibrium and detailed balance.An object...
applied to that surface element. It is generally true that the emissivity and absorptivity are properties of the material only, so that this equivalence will hold even when the radiation field is not thermal radiation. Kirchhoff's law also implies that the equilibrium distribution is unique, and Planck's contribution was to determine the expression of that equilibrium distribution.
Black body
A black body completely absorbs all of the electromagnetic radiation falling upon it (hence the term "black"). This means that , and by Kirchhoff's law, the emissivity will be unity as well, so that the thermal radiation from a black body is always equal to the full amount specified by Planck's law. In addition, it follows that no other body can emit thermal radiation that exceeds that of a black body, since if it were in equilibrium with a radiation field, it would be emitting more energy than was incident upon it.
, and by Kirchhoff's law, the emissivity will be unity as well, so that the thermal radiation from a black body is always equal to the full amount specified by Planck's law. In addition, it follows that no other body can emit thermal radiation that exceeds that of a black body, since if it were in equilibrium with a radiation field, it would be emitting more energy than was incident upon it.Though perfectly black materials do not exist, in practice a black surface can be accurately approximated. As to its material interior, a body is completely black to a certain wavelength if it is completely opaque to that wavelength; that means that it absorbs all of the wavelength that penetrates the interface to enter the body; this is not too difficult to achieve in practice. On the other hand, a perfectly black interface is not found in nature. The best practical way to make an effectively black interface is to simulate an 'interface' by use of a small hole in the wall of a large cavity in a completely opaque body, with a controlled temperature. Radiation entering the hole has almost no possibility of escaping the cavity without being absorbed by multiple impacts with its walls.
Lambert's cosine law
As explained by Planck, a radiating body has an interior consisting of matter, and an interface with its contiguous neighbouring material medium, which is usually the medium from within which the radiation from the surface of the body is observed. The interface is not composed of physical matter but is a theoretical conception, a mathematical two-dimensional surface, a joint property of the two contiguous media, strictly speaking belonging to neither separately. Such an interface can neither absorb nor emit, because it is not composed of physical matter; but it is the site of reflection and transmission of radiation, because it is a surface of discontinuity of optical properties. The reflection and transmission of radiation at the interface obey the Stokes–Helmholtz reciprocity principleHelmholtz reciprocity
The Helmholtz reciprocity principle describes how a ray of light and its reverse ray encounter matched optical adventures, such as reflections, refractions, and absorptions in a passive medium, or at an interface....
.
At any point in the interior of a black body located inside a cavity in thermodynamic equilibrium at temperature
 the radiation is homogeneous, isotropic and unpolarized. A black body absorbs all and reflects none of the electromagnetic radiation incident upon it. According to the Helmholtz reciprocity principle, radiation from the interior of a black body is not reflected at its surface, but is fully transmitted to its exterior. Because of the isotropy of the radiation in the body's interior, the spectral radiance of radiation transmitted from its interior to its exterior through its surface is independent of direction.
the radiation is homogeneous, isotropic and unpolarized. A black body absorbs all and reflects none of the electromagnetic radiation incident upon it. According to the Helmholtz reciprocity principle, radiation from the interior of a black body is not reflected at its surface, but is fully transmitted to its exterior. Because of the isotropy of the radiation in the body's interior, the spectral radiance of radiation transmitted from its interior to its exterior through its surface is independent of direction.This is expressed by saying that radiation from the surface of a black body in thermodynamic equilibrium obeys Lambert's cosine law. This means that the spectral flux from a given infinitesimal element of area
 of the emitting surface of the black body, measured from a given direction that makes an angle with the normal to the surface at , per unit solid angle of detection
of the emitting surface of the black body, measured from a given direction that makes an angle with the normal to the surface at , per unit solid angle of detection  , can be represented as
, can be represented as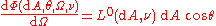
where denotes the spectral radiance that area would show if it were measured in its normal direction. For this equality, one is temporarily disregarding the fact that because the body is black the spectral radiance within it is the same in every direction.
But now taking into account the independence of direction of the spectral radiance of radiation from the surface of a black body in thermodynamic equilibrium, one has and so
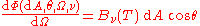 .
.This expresses the independence of direction of the spectral radiance of the surface of a black body in thermodynamic equilibrium.
Stefan–Boltzmann Law
The total power emitted per unit area at the surface of a black body (P) may be found by integrating the black body spectral flux found from Lambert's law over all frequencies, and over the solid angles corresponding to a hemisphere (h) above the surface.
The infinitesimal solid angle can be expressed in spherical polar coordinates:
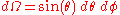
So that:
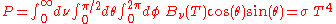
where
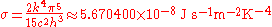
is known as the Stefan–Boltzmann constant.
Radiative transfer
The equation of radiative transfer describes the way in which radiation is affected as it travels through a material medium. For the special case in which the material medium is in thermodynamic equilibriumThermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
in the neighborhood of a point in the medium, Planck's law is of special importance.
For simplicity, we can consider the linear steady state, without scattering
Scattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
. The equation of radiative transfer states that for a beam of light going through a small distance ds, energy is conserved: The change in the (spectral) radiance
Radiance
Radiance and spectral radiance are radiometric measures that describe the amount of radiation such as light or radiant heat that passes through or is emitted from a particular area, and falls within a given solid angle in a specified direction. They are used to characterize both emission from...
of that beam (
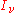 ) is equal to the amount removed by the material medium plus the amount gained from the material medium. If the radiation field is in equilibrium with the material medium, these two contributions will be equal. The material medium will have a certain emission coefficient and absorption coefficient.
) is equal to the amount removed by the material medium plus the amount gained from the material medium. If the radiation field is in equilibrium with the material medium, these two contributions will be equal. The material medium will have a certain emission coefficient and absorption coefficient.The absorption coefficient
 is the fractional change in the intensity of the light beam as it travels the distance ds, and has units of 1/length. It is composed of two parts, the decrease due to absorption and the increase due to stimulated emission
is the fractional change in the intensity of the light beam as it travels the distance ds, and has units of 1/length. It is composed of two parts, the decrease due to absorption and the increase due to stimulated emissionStimulated emission
In optics, stimulated emission is the process by which an atomic electron interacting with an electromagnetic wave of a certain frequency may drop to a lower energy level, transferring its energy to that field. A photon created in this manner has the same phase, frequency, polarization, and...
. Stimulated emission is emission by the material body which is caused by and is proportional to the incoming radiation. It is included in the absorption term because, like absorption, it is proportional to the intensity of the incoming radiation. Since the amount of absorption will generally vary linearly as the density
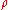 of the material, we may define a "mass absorption coefficient"
of the material, we may define a "mass absorption coefficient"  which is a property of the material itself. The change in intensity of a light beam due to absorption as it traverses a small distance ds will then be
which is a property of the material itself. The change in intensity of a light beam due to absorption as it traverses a small distance ds will then be 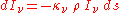
The "mass emission coefficient"
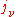 is equal to the radiance per unit volume of a small volume element divided by its mass (since, as for the mass absorption coefficient, the emission is proportional to the emitting mass) and has units of power/solid angle/frequency/density. Like the mass absorption coefficient, it too is a property of the material itself. The change in a light beam as it traverses a small distance ds will then be
is equal to the radiance per unit volume of a small volume element divided by its mass (since, as for the mass absorption coefficient, the emission is proportional to the emitting mass) and has units of power/solid angle/frequency/density. Like the mass absorption coefficient, it too is a property of the material itself. The change in a light beam as it traverses a small distance ds will then be 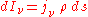
The equation of radiative transfer will then be the sum of these two contributions:
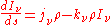
If the radiation field is in equilibrium with the material medium, then the radiation will be homogeneous (independent of position) so that
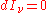 and:
and: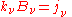
which is another statement of Kirchhoff's law, relating two material properties of the medium, and which yields the radiative transfer equation at a point around which the medium is in thermodynamic equilibrium:
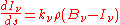
Einstein coefficients
The principle of detailed balanceDetailed balance
The principle of detailed balance is formulated for kinetic systems which are decomposed into elementary processes : At equilibrium, each elementary process should be equilibrated by its reverse process....
states that, at thermodynamic equilibrium, each elementary process is equilibrated by its reverse process.
In 1916, Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
applied this principle on an atomic level to the case of an atom radiating and absorbing radiation due to transitions between two particular energy levels, giving a deeper insight into the equation of radiative transfer and Kirchhoff's law for this type of radiation. If level 1 is the lower energy level with energy
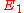 , and level 2 is the upper energy level with energy
, and level 2 is the upper energy level with energy 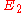 , then the frequency
, then the frequency  of the radiation radiated or absorbed will be determined by Bohr's frequency condition:
of the radiation radiated or absorbed will be determined by Bohr's frequency condition: 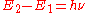 .
.If
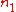 and
and  are the number densities of the atom in states 1 and 2 respectively, then the rate of change of these densities in time will be due to three processes:
are the number densities of the atom in states 1 and 2 respectively, then the rate of change of these densities in time will be due to three processes:  |
Spontaneous emission |
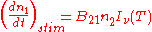 |
Stimulated emission |
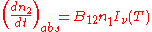 |
Photo-absorption |
where
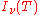 is the spectral radiance of the radiation field. The three parameters
is the spectral radiance of the radiation field. The three parameters 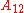 ,
, 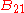 and
and 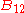 , known as the Einstein coefficients, are associated with the photon frequency
, known as the Einstein coefficients, are associated with the photon frequency  produced by the transition between two energy levels (states). As a result, each line in a spectra has it own set of associated coefficients. When the atoms and the radiation field are in equilibrium, the radiance will be given by Planck's law and, by the principle of detailed balance, the sum of these rates must be zero:
produced by the transition between two energy levels (states). As a result, each line in a spectra has it own set of associated coefficients. When the atoms and the radiation field are in equilibrium, the radiance will be given by Planck's law and, by the principle of detailed balance, the sum of these rates must be zero: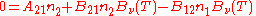
Since the atoms are also in equilibrium, the populations of the two levels are related by the Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
:
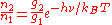
where
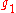 and
and 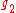 are the multiplicities of the respective energy levels. Combining the above two equations with the requirement that they be valid at any temperature yields two relationships between the Einstein coefficients:
are the multiplicities of the respective energy levels. Combining the above two equations with the requirement that they be valid at any temperature yields two relationships between the Einstein coefficients: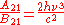
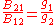
so that knowledge of one coefficient will yield the other two. For the case of isotropic absorption and emission, the emission coefficient (
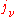 ) and absorption coefficient (
) and absorption coefficient (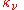 ) defined in the radiative transfer section above, can be expressed in terms of the Einstein coefficients. The relationships between the Einstein coefficients will yield the expression of Kirchhoff's law expressed in that section, namely that
) defined in the radiative transfer section above, can be expressed in terms of the Einstein coefficients. The relationships between the Einstein coefficients will yield the expression of Kirchhoff's law expressed in that section, namely that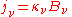
These coefficients apply to both atoms and molecules.
Limitations of Planck's Law
Planck's formula predicts that a black body will radiate energy at all frequencies, but its intensity rapidly tends to zero at both high and low frequencies (short and long wavelengths). For example, a black body at room temperature with one square meter of surface area will emit a photon in the visible range once every minute or so, meaning that for most practical purposes a black body at room temperature does not emit in the visible range.Balfour Stewart
In 1858, Balfour Stewart described his experiments on the thermal radiative emissive and absorptive powers of polished plates of various substances, compared with the powers of lamp-black surfaces, at the same temperature. Stewart chose lamp-black surfaces as his reference because of various previous experimental findings, especially those of Pierre PrevostPierre Prévost
Pierre Prévost was a Swiss philosopher and physicist. In he showed that all bodies radiate heat, no matter how hot or cold they are.-Life:...
and of John Leslie
John Leslie (physicist)
Sir John Leslie was a Scottish mathematician and physicist best remembered for his research into heat.Leslie gave the first modern account of capillary action in 1802 and froze water using an air-pump in 1810, the first artificial production of ice.In 1804, he experimented with radiant heat using...
. He wrote "Lamp-black, which absorbs all the rays that fall upon it, and therefore possesses the greatest possible absorbing power, will possess also the greatest possible radiating power." More an experimenter than a logician, Stewart failed to point out that his statement presupposed an abstract general principle, that there exist either ideally in theory or really in nature bodies or surfaces that respectively have one and the same unique universal greatest possible absorbing power, likewise for radiating power, for every wavelength and equilibrium temperature.
Stewart measured radiated power with a thermo-pile and sensitive galvanometer read with a microscope. He was concerned with selective thermal radiation, which he investigated with plates of substances that radiated and absorbed selectively for different qualities of radiation rather than maximally for all qualities of radiation. He discussed the experiments in terms of rays which could be reflected and refracted, and which obeyed the Stokes-Helmholtz reciprocity
Helmholtz reciprocity
The Helmholtz reciprocity principle describes how a ray of light and its reverse ray encounter matched optical adventures, such as reflections, refractions, and absorptions in a passive medium, or at an interface....
principle (though he did not use an eponym for it). He did not in this paper mention that the qualities of the rays might be described by their wavelengths, nor did he use spectrally resolving apparatus such as prisms or diffraction gratings. His work was quantitative within these constraints. He made his measurements in a room temperature environment, and quickly so as to catch his bodies in a condition near the thermal equilibrium in which they had been prepared by heating to equilibrium with boiling water. His measurements confirmed that substances that emit and absorb selectively respect the principle of selective equality of emission and absorption at thermal equilibrium.
Stewart offered a theoretical proof that this should be the case separately for every selected quality of thermal radiation, but his mathematics was not rigorously valid. He made no mention of thermodynamics in this paper, though he did refer to conservation of vis viva. He proposed that his measurements implied that radiation was both absorbed and emitted by particles of matter throughout depths of the media in which it propagated. He applied the Helmholtz reciprocity principle to account for the material interface processes as distinct from the processes in the interior material. He did not postulate unrealizable perfectly black surfaces. He concluded that his experiments showed that in a cavity in thermal equilibrium, the heat radiated from any part of the interior bounding surface, no matter of what material it might be composed, was the same as would have been emitted from a surface of the same shape and position that would have been composed of lamp-black. He did not state explicitly that the lamp-black-coated bodies that he used as reference must have had a unique common spectral emittance function that depended on temperature in a unique way.
Gustav Kirchhoff
In 1859, not knowing of Stewart's work, Gustav Robert Kirchhoff reported the coincidence of the wavelengths of spectrally resolved lines of absorption and of emission of visible light.Kirchhoff then went on to consider bodies that emit and absorb heat radiation, in an opaque enclosure or cavity, in equilibrium at temperature .
Here is used a notation different from Kirchhoff's. Here, the emitting power denotes a dimensioned quantity, the total radiation emitted by a body labeled by index at temperature . The total absorption ratio of that body is dimensionless, the ratio of absorbed to incident radiation in the cavity at temperature . (In contrast with Balfour Stewart's, Kirchhoff's definition of his absorption ratio did not refer in particular to a lamp-black surface as the source of the incident radiation.) Thus the ratio of emitting power to absorption ratio is a dimensioned quantity, with the dimensions of emitting power, because is dimensionless. Also here the wavelength-specific emitting power of the body at temperature is denoted by and the wavelength-specific absorption ratio by . Again, the ratio of emitting power to absorption ratio is a dimensioned quantity, with the dimensions of emitting power.
In a second report made in 1859, Kirchhoff announced a new general principle or law for which he offered a theoretical and mathematical proof, though he did not offer quantitative measurements of radiation powers. His theoretical proof was and still is considered by some writers to be invalid. His principle, however, has endured: it was that for heat rays of the same wavelength, in equilibrium at at a given temperature, the wavelength-specific ratio of emitting power to absorption ratio has one and the same common value for all bodies that emit and absorb at that wavelength. In symbols, the law stated that the wavelength-specific ratio has one and the same value for all bodies, that is for all values of index . In this report there was no mention of black bodies.
In 1860, still not knowing of Stewart's measurements for selected qualities of radiation, Kirchhoff pointed out that it was long established experimentally that for total heat radiation, of unselected quality, emitted and absorbed by a body in equilibrium, the dimensioned total radiation ratio , has one and the same value common to all bodies, that is, for every value of the material index . Again without measurements of radiative powers or other new experimental data, Kirchhoff then offered a fresh theoretical proof of his new principle of the universality of the value of the wavelength-specific ratio at thermal equilibrium. His fresh theoretical proof was and still is considered by some writers to be invalid.
But more importantly, it relied on a new theoretical postulate of "perfectly black bodies". Such black bodies showed complete absorption in their infinitely thin most superficial surface. They correspond to Balfour Stewart's reference bodies, with internal radiation, coated with lamp-black. They were not the more realistic perfectly black bodies later considered by Planck. Planck's black bodies radiated and absorbed only by the material in their interiors; their interfaces with contiguous media were only mathematical surfaces, capable neither of absorption nor emission, but only of reflecting and transmitting with refraction.
Kirchhoff's proof considered an arbitrary non-ideal body labeled as well as various perfect black bodies labeled . It required that the bodies be kept in a cavity in thermal equilibrium at temperature . His proof intended to show that the ratio was independent of the nature of the non-ideal body, however partly transparent or partly reflective it was.
His proof first argued that for wavelength and at temperature , at thermal equilibrium, all perfectly black bodies of the same size and shape have the one and the same common value of emissive power , with the dimensions of power. His proof noted that the dimensionless wavelength-specific absorption ratio of a perfectly black body is by definition exactly 1. Then for a perfectly black body, the wavelength-specific ratio of emissive power to absorption ratio is again just , with the dimensions of power. Kirchhoff considered, successively, thermal equilibrium with the arbitrary non-ideal body, and with a perfectly black body of the same size and shape, in place in his cavity in equilibrium at temperature . He argued that the flows of heat radiation must be the same in each case. Thus he argued that at thermal equilibrium the ratio was equal to , which may now be denoted , a continuous function, dependent only on at fixed temperature , and an increasing function of at fixed wavelength , at low temperatures vanishing for visible but not for longer wavelengths, with positive values for visible wavelengths at higher temperatures, which does not depend on the nature of the arbitrary non-ideal body. (Geometrical factors, taken into detailed account by Kirchhoff, have been ignored in the foregoing.)
Thus Kirchhoff's law of thermal radiation can be stated: "For any material at all , radiating and absorbing in thermodynamic equilibrium at any given temperature , for every wavelength , the ratio of emissive power to absorptive ratio has one universal value, which is characteristic of a perfect black body, and is an emissive power which we here represent by ." (For our notation , Kirchhoff's original notation was simply .)
Kirchhoff announced that the determination of the function was a problem of the highest importance, though he recognized that there would be experimental difficulties to be overcome. He supposed that like other functions that do not depend on the properties of individual bodies, it would be a simple function. That function has occasionally been called 'Kirchhoff's (emission, universal) function', though its precise mathematical form would not be known for another forty years, till it was discovered by Planck in 1900. The theoretical proof for Kirchhoff's universality principle was worked on and debated by various physicists over the same time, and later. Kirchhoff stated later in 1860 that his theoretical proof was better than Balfour Stewart's, and in some respects it was so. Kirchhoff's 1860 paper did not mention the second law of thermodynamics, and of course did not mention the concept of entropy which had not at that time been established. According to Helge Kragh, "Quantum theory owes its origin to the study of thermal radiation, in particular to the "blackbody" radiation the Robert Kirchhoff had first defined in 1859–1860."
Empirical sources of Planck's law
In 1860, Kirchhoff predicted experimental difficulties for the empirical determination of the function that described the dependence of the black-body spectrum as a function only of temperature and wavelength. And so it turned out. It took some forty years of development of improved methods of measurement of electromagnetic radiation to get a reliable result.In 1865, John Tyndall
John Tyndall
John Tyndall FRS was a prominent Irish 19th century physicist. His initial scientific fame arose in the 1850s from his study of diamagnetism. Later he studied thermal radiation, and produced a number of discoveries about processes in the atmosphere...
described radiation from electrically heated filaments and from carbon arcs as visible and invisible. Tyndall spectrally decomposed the radiation by use of a rock salt prism, which passed heat as well as visible rays, and measured the radiation intensity by means of a thermopile.
In 1880, André-Prosper-Paul Crova published a diagram of the three-dimensional appearance of the graph of the strength of thermal radiation as a function of wavelength and temperature.
Finding the empirical law
Max PlanckMax Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
originally produced his law on 19 October 1900 as an improvement upon the Wien approximation, published in 1896 by Wilhelm Wien
Wilhelm Wien
Wilhelm Carl Werner Otto Fritz Franz Wien was a German physicist who, in 1893, used theories about heat and electromagnetism to deduce Wien's displacement law, which calculates the emission of a blackbody at any temperature from the emission at any one reference temperature.He also formulated an...
, which fit the experimental data at short wavelengths (high frequencies) but deviated from it at long wavelengths (low frequencies). In June 1900, based on heuristic theoretical considerations, Rayleigh had suggested a formula that he proposed might be checked experimentally. The suggestion was that the Stewart–Kirchhoff universal function might be of the form
 . This was not the celebrated Rayleigh–Jeans formula
. This was not the celebrated Rayleigh–Jeans formula 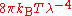 , which did not emerge until 1905, though it did reduce to the latter for long wavelengths, which are the relevant ones here. According to Klein, one may speculate that it is likely that Planck had seen this suggestion though he did not mention it in his papers of 1900 and 1901. Planck would have been aware of various other proposed formulas which had been offered. On 7 October 1900, Rubens told Planck that in the complementary domain (long wavelength, low frequency), and only there, Rayleigh's 1900 formula fitted the observed data well.
, which did not emerge until 1905, though it did reduce to the latter for long wavelengths, which are the relevant ones here. According to Klein, one may speculate that it is likely that Planck had seen this suggestion though he did not mention it in his papers of 1900 and 1901. Planck would have been aware of various other proposed formulas which had been offered. On 7 October 1900, Rubens told Planck that in the complementary domain (long wavelength, low frequency), and only there, Rayleigh's 1900 formula fitted the observed data well.For long wavelengths, Rayleigh's 1900 heuristic formula approximately meant that energy was proportional to temperature, . It is known that
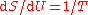 and this leads to
and this leads to 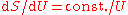 and thence to for long wavelengths. But for short wavelengths, the Wien formula leads to and thence to for short wavelengths. Planck perhaps patched together these two heuristic formulas, for long and for short wavelengths, to produce a formula
and thence to for long wavelengths. But for short wavelengths, the Wien formula leads to and thence to for short wavelengths. Planck perhaps patched together these two heuristic formulas, for long and for short wavelengths, to produce a formula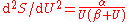
This led Planck to the formula
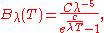
where Planck used the symbols
 and
and  to denote empirical fitting constants.
to denote empirical fitting constants.Planck sent this result to Rubens, who compared it with his and Kurlbaum's observational data and found that it fitted for all wavelengths remarkably well. On 19 October 1900, Rubens and Kurlbaum briefly reported the fit to the data, and Planck added a short presentation to give a theoretical sketch to account for his formula. Within a week, Rubens and Kurlbaum gave a fuller report of their measurements confirming Planck's law. Their technique for spectral resolution of the longer wavelength radiation was called the residual ray method. The rays were repeatedly reflected from polished crystal surfaces, and the rays that made it all the way through the process were 'residual', and were of wavelengths preferentially reflected by crystals of suitably specific materials.
Trying to find a physical explanation of the law
Once Planck had discovered the empirically fitting function, he constructed a physical derivation of this law. His thinking revolved around entropy rather than being directly about temperature. Planck's logic started by postulating a universal finite element of hypervolume of statistical phase space. Consequent on this, he considered a cavity with perfectly reflective walls; the cavity contained finitely many hypothetical well separated resonant oscillatory bodies, several such oscillators at each of finitely many characteristic frequencies. The hypothetical oscillators were for Planck purely imaginary theoretical investigative probes, and he said of them that such oscillators do not need to "really exist somewhere in nature, provided their existence and their properties are consistent with the laws of thermodynamics and electrodynamics.". Beyond their occupation of the universal hypervolume elements of statistical phase space, Planck did not attribute any definite physical significance to his hypothesis of resonant oscillators, but rather proposed it as a mathematical device that enabled him to derive a single expression for the black body spectrum that matched the empirical data at all wavelengths. He tentatively mentioned the possible connection of such oscillators with atoms. In a sense, the oscillators corresponded to Planck's speck of carbon; the size of the speck could be small regardless of the size of the cavity, provided the speck effectively transduced energy between radiative wavelength modes.Partly following a heuristic method of calculation pioneered by Boltzmann for gas molecules, Planck considered the possible ways of distributing electromagnetic energy over the different modes of his hypothetical charged material oscillators, heuristically distributing the energy in arbitrary merely mathematical quanta ϵ, which Boltzmann would have proceeded to make tend to zero in magnitude. Referring to a new universal constant of nature, h, Planck supposed that, in the several oscillators of each of the finitely many characteristic frequencies, the total energy was distributed to each in an integer multiple of a definite physical unit of energy, ϵ, not arbitrary as in Boltzmann's method, but now for Planck characteristic of the respective characteristic frequency. His new universal constant of nature, h, is now known as Planck's constant.
Planck explained further that the respective definite unit, ϵ, of energy should be proportional to the respective characteristic oscillation frequency
 of the hypothetical oscillator, and in 1901 he expressed this with the constant of proportionality h:
of the hypothetical oscillator, and in 1901 he expressed this with the constant of proportionality h: .
.This is known as Planck's relation.
Planck made no assumption that light propagates in free space as particles; he did not quantize light as it propagated. This may be seen by reading his 1901 paper. He plainly explains in his book "Theory of Heat Radiation" that his constant refers to hypothetical material Hertzian oscillators. The idea of quantization of the free electromagnetic radiative field was developed by others and was eventually incorporated into what we now know as quantum mechanics.
In 1906, Planck acknowledged that his imaginary resonators, having linear dynamics, did not provide a physical explanation for energy transduction between frequencies. Planck was careful to point out that, in a cavity with perfectly reflecting walls and containing no ponderable matter to transduce energy between frequency components, the free electromagnetic field cannot exchange energy between frequency components. This is because of the linearity of Maxwell's laws. Such a field is not within the scope of the classical principle of equipartition of energy, which it accordingly neither obeys nor violates. That is to say, Planck believed that the classical equipartition theorem does not refer to such a field, which remains whatever was introduced and does not evolve into a black body field. Thus, the linearity of his mechanical assumptions precluded Planck from having a mechanical explanation of the maximization of the entropy of the thermodynamic equilibrium thermal radiation field. This is why he had to resort to Boltzmann's probabilistic arguments.
Planck's law may be regarded as fulfulling the prediction of Gustav Kirchhoff
Gustav Kirchhoff
Gustav Robert Kirchhoff was a German physicist who contributed to the fundamental understanding of electrical circuits, spectroscopy, and the emission of black-body radiation by heated objects...
that his law of thermal radiation
Kirchhoff's law of thermal radiation
In thermodynamics, Kirchhoff's law of thermal radiation, or Kirchhoff's law for short, is a general statement equating emission and absorption in heated objects, proposed by Gustav Kirchhoff in 1859, following from general considerations of thermodynamic equilibrium and detailed balance.An object...
was of the highest importance. In his mature presentation of his own law, Planck offered a thorough and detailed theoretical proof for Kirchhoff's law, theoretical proof of which until then had been sometimes debated, partly because it was said to rely on unphysical theoretical objects, such as Kirchhoff's perfectly absorbing infinitely thin black surface.
Subsequent events
It was not till five years after Planck made his heuristic assumption of abstract elements of energy or of action that Albert EinsteinAlbert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
conceived of really existing quanta
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
of light in 1905 as a revolutionary explanation of black-body radiation, of photoluminescence, of the photoelectric effect
Photoelectric effect
In the photoelectric effect, electrons are emitted from matter as a consequence of their absorption of energy from electromagnetic radiation of very short wavelength, such as visible or ultraviolet light. Electrons emitted in this manner may be referred to as photoelectrons...
, and of the ionization of gases by ultraviolet light. In 1905, "Einstein believed that Planck's theory could not be made to agree with the idea of light quanta, a mistake he corrected in 1906." Contrary to Planck's beliefs of the time, Einstein proposed a model and formula whereby light was emitted, absorbed, and propagated in free space in energy quanta localized in points of space. As an introduction to his reasoning, Einstein recapitulated Planck's model of hypothetical resonant material electric oscillators as sources and sinks of radiation, but then he offered a new argument, disconnected from that model, but partly based on a thermodynamic argument of Wien, in which Planck's formula ϵ =
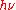 played no role. Einstein gave the energy content of such quanta in the form
played no role. Einstein gave the energy content of such quanta in the form 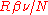 . Thus Einstein was contradicting the undulatory theory of light held by Planck. In 1910, criticizing a manuscript sent to him by Planck, knowing that Planck was a steady supporter of Einstein's theory of special relativity, Einstein wrote to Planck: "To me it seems absurd to have energy continuously distributed in space without assuming an aether."
. Thus Einstein was contradicting the undulatory theory of light held by Planck. In 1910, criticizing a manuscript sent to him by Planck, knowing that Planck was a steady supporter of Einstein's theory of special relativity, Einstein wrote to Planck: "To me it seems absurd to have energy continuously distributed in space without assuming an aether."According to Thomas Kuhn, it was not till 1908 that Planck more or less accepted part of Einstein's arguments for physical as distinct from abstract mathematical discreteness in thermal radiation physics. Still in 1908, considering Einstein's proposal of quantal propagation, Planck opined that such a revolutionary step was perhaps unnecessary. Until then, Planck had been consistent in thinking that discreteness of action quanta was to be found neither in his resonant oscillators nor in the propagation of thermal radiation. Kuhn wrote that, in Planck's earlier papers and in his 1906 monograph, there is no "mention of discontinuity, [nor] of talk of a restriction on oscillator energy, [nor of] any formula like ." Kuhn pointed out that his study of Planck's papers of 1900 and 1901, and of his monograph of 1906, had led him to "heretical" conclusions, contrary to the widespread assumptions of others who saw Planck's writing only from the perspective of later, anachronistic, viewpoints. Kuhn's conclusions, finding a period till 1908, when Planck consistently held his 'first theory', have been accepted by other historians.
In the second edition of his monograph, in 1912, Planck sustained his dissent from Einstein's proposal of light quanta. He proposed in some detail that absorption of light by his virtual material resonators might be continuous, occurring at a constant rate in equilibrium, as distinct from quantal absorption. Only emission was quantal. This has at times been called Planck's "second theory".
It was not till 1919 that Planck in the third edition of his monograph more or less accepted his 'third theory', that both emission and absorption of light were quantal.
The colourful term "ultraviolet catastrophe
Ultraviolet catastrophe
The ultraviolet catastrophe, also called the Rayleigh–Jeans catastrophe, was a prediction of late 19th century/early 20th century classical physics that an ideal black body at thermal equilibrium will emit radiation with infinite power....
" was given by Paul Ehrenfest
Paul Ehrenfest
Paul Ehrenfest was an Austrian and Dutch physicist, who made major contributions to the field of statistical mechanics and its relations with quantum mechanics, including the theory of phase transition and the Ehrenfest theorem.- Biography :Paul Ehrenfest was born and grew up in Vienna in a Jewish...
in 1911 to the paradoxical result that the total energy in the cavity tends to infinity when the equipartition theorem
Equipartition theorem
In classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition...
of classical statistical mechanics is (mistakenly) applied to black body radiation. But this had not been part of Planck's thinking, because he had not tried to apply the doctrine of equipartition: he had not noticed any sort of "catastrophe"—it was noted by Lord Rayleigh in 1900, and in 1901 by Sir James Jeans; and later, in 1905, by Einstein when he wanted to support the idea that light propagates as discrete packets, later called 'photons', and by Rayleigh and by Jeans.
In 1913, Bohr gave another formula with a further different physical meaning to the quantity
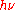 . In contrast to Planck's and Einstein's formulas, Bohr's formula referred explicitly and categorically to energy levels of atoms. Bohr's formula was
. In contrast to Planck's and Einstein's formulas, Bohr's formula referred explicitly and categorically to energy levels of atoms. Bohr's formula was  where
where 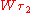 and
and  denote the energy levels of quantum states of an atom, with quantum numbers
denote the energy levels of quantum states of an atom, with quantum numbers 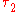 and
and 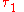 . The symbol
. The symbol  denotes the frequency of a quantum of radiation that can be emitted or absorbed as the atom passes between those two quantum states. In contrast to Planck's model, the frequency
denotes the frequency of a quantum of radiation that can be emitted or absorbed as the atom passes between those two quantum states. In contrast to Planck's model, the frequency  has no immediate relation to frequencies that might describe those quantum states themselves.
has no immediate relation to frequencies that might describe those quantum states themselves.Later, in 1924, Satyendra Nath Bose
Satyendra Nath Bose
Satyendra Nath Bose FRS was an Indian mathematician and physicist noted for his collaboration with Albert Einstein in developing a theory regarding the gaslike qualities of electromagnetic radiation. He is best known for his work on quantum mechanics in the early 1920s, providing the foundation...
developed the theory of the statistical mechanics of photons, which allowed a theoretical derivation
Gas in a box
In quantum mechanics, the results of the quantum particle in a box can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions...
of Planck's law. The actual word 'photon' was invented still later, by G.N. Lewis in 1926, who mistakenly believed that photons were conserved, contrary to Bose–Einstein statistics; nevertheless the word 'photon' was adopted to express the Einstein postulate of the packet nature of light propagation. In an electromagnetic field isolated in a vacuum in a vessel with perfectly reflective walls, such as was considered by Planck, indeed the photons would be conserved according to Einstein's 1905 model, but Lewis was referring to a field of photons considered as a system closed with respect to ponderable matter but open to exchange of electromagnetic energy with a surrounding system of ponderable matter, and he mistakenly imagined that still the photons were conserved, being stored inside atoms.
Ultimately, Planck's law of black-body radiation contributed to Einstein's concept of quanta of light carrying linear momentum, which became the fundamental basis for the development of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
The above-mentioned linearity of Planck's mechanical assumptions, not allowing for energetic interactions between frequency components, was superseded in 1925 by Heisenberg's original quantum mechanics. In his paper submitted on 29 July 1925, Heisenberg's theory accounted for Bohr's above-mentioned formula of 1913. It admitted non-linear oscillators as models of atomic quantum states, allowing energetic interaction between their own multiple internal discrete Fourier frequency components, on the occasions of emission or absorption of quanta of radiation. The frequency of a quantum of radiation was that of a definite coupling between internal atomic meta-stable oscillatory quantum states. At that time, Heisenberg knew nothing of matrix albegra, but Max Born
Max Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
read the manuscript of Heisenberg's paper and recognized the matrix character of Heisenberg's theory. Then Born and Jordan
Pascual Jordan
-Further reading:...
published an explicitly matrix theory of quantum mechanics, based on, but in form distinctly different from, Heisenberg's original quantum mechanics; it is the Born and Jordan matrix theory that is today called matrix mechanics.
Nowadays, as a statement of the energy of a light quantum, often one finds the formula E = ħω, where ħ = h/2π, and ω =
 denotes angular frequency, and less often the equivalent formula E =
denotes angular frequency, and less often the equivalent formula E = 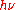 . This statement about a really existing and propagating light quantum, based on Einstein's, has a physical meaning different from that of Planck's above statement ϵ =
. This statement about a really existing and propagating light quantum, based on Einstein's, has a physical meaning different from that of Planck's above statement ϵ = 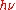 about the abstract energy units to be distributed amongst his hypothetical resonant material oscillators.
about the abstract energy units to be distributed amongst his hypothetical resonant material oscillators.An article by Helge Kragh published in Physics World
Physics World
Physics World is the membership magazine of the Institute of Physics, one of the largest physical societies in the world. It is an international monthly magazine covering all areas of physics, both pure and applied, and is aimed at physicists in research, industry and education worldwide...
gives an account of this history.
External links
- Summary of Radiation
- Radiation of a Blackbody – interactive simulation to play with Planck's law
- Scienceworld entry on Planck's Law
- Dimensionless Constants and Blackbody Radiation Laws

