
Pati-Salam model
Encyclopedia
In physics
, the Pati–Salam model is a Grand Unification Theory
(GUT) was proposed in 1974 by nobel laureate Abdus Salam
and Jogesh Pati
. The unification is based on there being four quark
color charge
s, dubbed red, green, blue and violet (or lilac), instead of the conventional three, with the new "violet" quark being identified with the lepton
s. The model also has Left–right symmetry and predicts the existence of a high energy right handed weak interaction
with heavy W' and Z' bosons
.
Originally the fourth color was labelled "lilac" to alliterate with "lepton" Pati-Salam is a mainstream theory and a viable alternative to the Georgi–Glashow SU(5) unification. It can be embedded within an SO(10) unification model
(as can SU(5)).
or ( SU(4) × SU(2)L× SU(2)R ) / Z2
and the fermions form three families, each consisting of the representations (4,2,1) and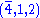 . This needs some explanation. The center
. This needs some explanation. The center
of SU(4)× SU(2)L× SU(2)R is Z4× Z2L× Z2R. The Z2 in the quotient refers to the two element subgroup generated by the element of the center corresponding to the 2 element of Z4 and the 1 elements of Z2L and Z2R. This includes the right-handed neutrino, which is now likely believed to exist. See neutrino oscillation
s. There is also a (4,1,2) and/or a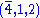 scalar field
scalar field
called the Higgs field which acquires a VEV. This results in a spontaneous symmetry breaking
from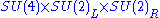 to
to 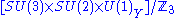 or from
or from 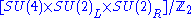 to
to 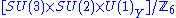 and also,
and also,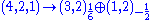 (q and l),
(q and l),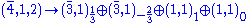 (dc, uc, ec and νc),
(dc, uc, ec and νc),
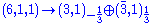 ,
,  and
and 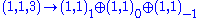 . See restricted representation
. See restricted representation
. Of course, calling the representations things like and (6,1,1) is purely a physicist's convention, not a mathematician's convention, where representations are either labelled by Young tableau
and (6,1,1) is purely a physicist's convention, not a mathematician's convention, where representations are either labelled by Young tableau
x or Dynkin diagrams with numbers on their vertices, but still, it is standard among GUT theorists.
The weak hypercharge
, Y, is the sum of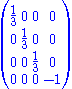 of SU(4) and
of SU(4) and 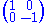 of SU(2)R
of SU(2)R
Actually, it is possible to extend the Pati-Salam group so that it has two connected component
s. The relevant group is now the semidirect product
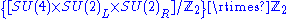 . The last Z2 also needs explaining. It corresponds to an automorphism
. The last Z2 also needs explaining. It corresponds to an automorphism
of the (unextended) Pati-Salam group which is the composition
of an involutive outer automorphism of SU(4) which isn't an inner automorphism
with interchanging the left and right copies of SU(2). This explains the name left and right and is one of the main motivations for originally studying this model. This extra "left-right symmetry
" restores the concept of parity
which had been shown not to hold at low energy scales for the weak interaction
. In this extended model, is an irrep and so is
is an irrep and so is 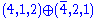 . This is the simplest extension of the minimal left-right model unifying QCD
. This is the simplest extension of the minimal left-right model unifying QCD
with B−L.
Since the homotopy group
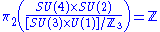 , this model predicts monopoles. See 't Hooft-Polyakov monopole
, this model predicts monopoles. See 't Hooft-Polyakov monopole
.
This model was invented by Jogesh Pati
and Abdus Salam
.
This model doesn't predict gauge mediated proton decay
(unless it is embedded within an even larger GUT group).
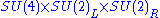 and U(1)R invariant cubic polynomial in the superfields. It is a linear combination of the following terms:
and U(1)R invariant cubic polynomial in the superfields. It is a linear combination of the following terms:
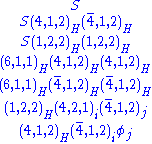
 and
and  are the generation indices.
are the generation indices.
. For that, we need the additional chiral multiplets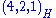 and
and 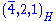
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Pati–Salam model is a Grand Unification Theory
Grand unification theory
The term Grand Unified Theory, often abbreviated as GUT, refers to any of several similar candidate models in particle physics in which at high-energy, the three gauge interactions of the Standard Model which define the electromagnetic, weak, and strong interactions, are merged into one single...
(GUT) was proposed in 1974 by nobel laureate Abdus Salam
Abdus Salam
Mohammad Abdus Salam, NI, SPk Mohammad Abdus Salam, NI, SPk Mohammad Abdus Salam, NI, SPk (Urdu: محمد عبد السلام, pronounced , (January 29, 1926– November 21, 1996) was a Pakistani theoretical physicist and Nobel laureate in Physics for his work on the electroweak unification of the...
and Jogesh Pati
Jogesh Pati
Jogesh C. Pati is an Indian American theoretical physicist at the University of Maryland, College Park.-Biography:...
. The unification is based on there being four quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
color charge
Color charge
In particle physics, color charge is a property of quarks and gluons that is related to the particles' strong interactions in the theory of quantum chromodynamics . Color charge has analogies with the notion of electric charge of particles, but because of the mathematical complications of QCD,...
s, dubbed red, green, blue and violet (or lilac), instead of the conventional three, with the new "violet" quark being identified with the lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
s. The model also has Left–right symmetry and predicts the existence of a high energy right handed weak interaction
Weak interaction
Weak interaction , is one of the four fundamental forces of nature, alongside the strong nuclear force, electromagnetism, and gravity. It is responsible for the radioactive decay of subatomic particles and initiates the process known as hydrogen fusion in stars...
with heavy W' and Z' bosons
W' and Z' bosons
In particle physics, W' and Z' bosons refer to hypothetical new gauge bosons that arise from extensions of the electroweak symmetry of the Standard Model. They are named in analogy with the Standard Model W and Z bosons....
.
Originally the fourth color was labelled "lilac" to alliterate with "lepton" Pati-Salam is a mainstream theory and a viable alternative to the Georgi–Glashow SU(5) unification. It can be embedded within an SO(10) unification model
SO(10) (physics)
In particle physics, one of the grand unified theories is based on the SO Lie group....
(as can SU(5)).
Core theory
The Pati–Salam model states that the gauge group is either SU(4) × SU(2)L× SU(2)RSpecial unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
or ( SU(4) × SU(2)L× SU(2)R ) / Z2
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
and the fermions form three families, each consisting of the representations (4,2,1) and
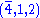 . This needs some explanation. The center
. This needs some explanation. The centerCenter (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of SU(4)× SU(2)L× SU(2)R is Z4× Z2L× Z2R. The Z2 in the quotient refers to the two element subgroup generated by the element of the center corresponding to the 2 element of Z4 and the 1 elements of Z2L and Z2R. This includes the right-handed neutrino, which is now likely believed to exist. See neutrino oscillation
Neutrino oscillation
Neutrino oscillation is a quantum mechanical phenomenon predicted by Bruno Pontecorvowhereby a neutrino created with a specific lepton flavor can later be measured to have a different flavor. The probability of measuring a particular flavor for a neutrino varies periodically as it propagates...
s. There is also a (4,1,2) and/or a
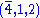 scalar field
scalar fieldScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
called the Higgs field which acquires a VEV. This results in a spontaneous symmetry breaking
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
from
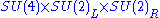 to
to 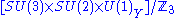 or from
or from 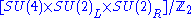 to
to 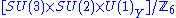 and also,
and also,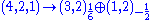 (q and l),
(q and l),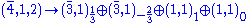 (dc, uc, ec and νc),
(dc, uc, ec and νc),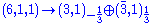 ,
,  and
and 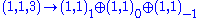 . See restricted representation
. See restricted representationRestricted representation
In mathematics, restriction is a fundamental construction in representation theory of groups. Restriction forms a representation of a subgroup from a representation of the whole group. Often the restricted representation is simpler to understand...
. Of course, calling the representations things like
 and (6,1,1) is purely a physicist's convention, not a mathematician's convention, where representations are either labelled by Young tableau
and (6,1,1) is purely a physicist's convention, not a mathematician's convention, where representations are either labelled by Young tableauYoung tableau
In mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at...
x or Dynkin diagrams with numbers on their vertices, but still, it is standard among GUT theorists.
The weak hypercharge
Weak hypercharge
The weak hypercharge in particle physics is a conserved quantum number relating the electrical charge and the third component of weak isospin, and is similar to the Gell-Mann–Nishijima formula for the hypercharge of strong interactions...
, Y, is the sum of
 of SU(4) and
of SU(4) and 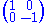 of SU(2)R
of SU(2)RActually, it is possible to extend the Pati-Salam group so that it has two connected component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
s. The relevant group is now the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
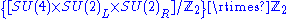 . The last Z2 also needs explaining. It corresponds to an automorphism
. The last Z2 also needs explaining. It corresponds to an automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of the (unextended) Pati-Salam group which is the composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of an involutive outer automorphism of SU(4) which isn't an inner automorphism
Inner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
with interchanging the left and right copies of SU(2). This explains the name left and right and is one of the main motivations for originally studying this model. This extra "left-right symmetry
Left-right symmetry
Left–right symmetry is a general principle in physics which holds that valid physical laws must not produce a different result for a motion that is left-handed than motion that is right-handed...
" restores the concept of parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
which had been shown not to hold at low energy scales for the weak interaction
Weak interaction
Weak interaction , is one of the four fundamental forces of nature, alongside the strong nuclear force, electromagnetism, and gravity. It is responsible for the radioactive decay of subatomic particles and initiates the process known as hydrogen fusion in stars...
. In this extended model,
 is an irrep and so is
is an irrep and so is 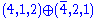 . This is the simplest extension of the minimal left-right model unifying QCD
. This is the simplest extension of the minimal left-right model unifying QCDQuantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
with B−L.
Since the homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
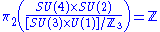 , this model predicts monopoles. See 't Hooft-Polyakov monopole
, this model predicts monopoles. See 't Hooft-Polyakov monopole't Hooft-Polyakov monopole
In theoretical physics, the t Hooft–Polyakov monopole is a topological soliton similar to the Dirac monopole but without any singularities. It arises in the case of a Yang–Mills theory with a gauge group G, coupled to a Higgs field which spontaneously breaks it down to a smaller group H via the...
.
This model was invented by Jogesh Pati
Jogesh Pati
Jogesh C. Pati is an Indian American theoretical physicist at the University of Maryland, College Park.-Biography:...
and Abdus Salam
Abdus Salam
Mohammad Abdus Salam, NI, SPk Mohammad Abdus Salam, NI, SPk Mohammad Abdus Salam, NI, SPk (Urdu: محمد عبد السلام, pronounced , (January 29, 1926– November 21, 1996) was a Pakistani theoretical physicist and Nobel laureate in Physics for his work on the electroweak unification of the...
.
This model doesn't predict gauge mediated proton decay
Proton decay
In particle physics, proton decay is a hypothetical form of radioactive decay in which the proton decays into lighter subatomic particles, such as a neutral pion and a positron...
(unless it is embedded within an even larger GUT group).
Gauge symmetry group
[SU(4)× SU(2)L × SU(2)R]/Z2Vector superfields
Those associated with the SU(4)× SU(2)L × SU(2)R gauge symmetryChiral superfields
As complex representations:| label | description | multiplicity | SU(4)×SU(2)L× SU(2)R rep | R | A |
|---|---|---|---|---|---|
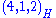 |
GUT Higgs field | 1 | 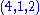 |
0 | 0 |
 |
GUT Higgs field | 1 | 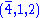 |
0 | 0 |
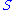 |
singlet | 1 | 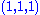 |
2 | 0 |
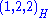 |
electroweak Higgs field | 1 | 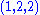 |
0 | 0 |
 |
no name | 1 | 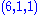 |
2 | 0 |
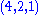 |
matter field | 3 | 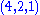 |
1 | 1 |
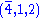 |
matter field | 3 | 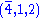 |
1 | |
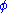 |
sterile neutrino | 3 | 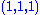 |
1 | 1 |
Superpotential
A generic invariant renormalizable superpotential is a (complex)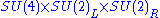 and U(1)R invariant cubic polynomial in the superfields. It is a linear combination of the following terms:
and U(1)R invariant cubic polynomial in the superfields. It is a linear combination of the following terms: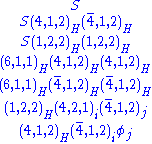
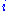 and
and 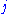 are the generation indices.
are the generation indices.Left-right extension
We can extend this model to include left-right symmetryLeft-right symmetry
Left–right symmetry is a general principle in physics which holds that valid physical laws must not produce a different result for a motion that is left-handed than motion that is right-handed...
. For that, we need the additional chiral multiplets
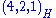 and
and 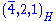
Sources
- Graham G. Ross, Grand Unified Theories, Benjamin/Cummings, 1985, ISBN 0-8053-6968-6
- Anthony Zee, Quantum Field Theory in a Nutshell, Princeton U. Press, Princeton, 2003, ISBN 0-691-01019-6
External links
- Pati-Salam model on Scholarpedia
- Proton decay, annihilation or fusion? by Wu, Dan-Di; Li, Tie-Zhong, Zeitschrift für Physik C, Volume 27, Issue 2, pp. 321–323 preview Fusion of all three quarks is the only decay mechanism mediated by the Higgs particle, not the gauge bosons, in the Pati-Salam modelPati-Salam modelIn physics, the Pati–Salam model is a Grand Unification Theory was proposed in 1974 by nobel laureate Abdus Salam and Jogesh Pati. The unification is based on there being four quark color charges, dubbed red, green, blue and violet , instead of the conventional three, with the new "violet" quark...
- The Algebra of Grand Unified Theories John Huerta. Slide show: contains an overview of Pati-Salam
- the Pati-Salam model Motivation for the Pati–Salam model

