
Definite bilinear form
Encyclopedia
In mathematics
, a definite bilinear form is a bilinear form B over some vector space
V (with real
or complex
scalar
field
) such that the associated quadratic form

is definite
, that is, has a real
value with the same sign
(positive or negative) for all non-zero x. According to that sign, B is called positive definite or negative definite. If Q takes both positive and negative values, the bilinear form B is called indefinite.
If B(x, x) ≥ 0 for all x, B is said to be positive semidefinite. Negative semidefinite bilinear forms are defined similarly.
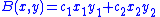
where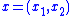 ,
, 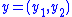 , and
, and 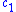 and
and 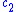 are constants. If
are constants. If 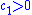 and
and  , the bilinear form
, the bilinear form  is positive definite. If one of the constants is positive and the other is zero, then
is positive definite. If one of the constants is positive and the other is zero, then  is positive semidefinite. If
is positive semidefinite. If 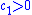 and
and  , then
, then  is indefinite.
is indefinite.
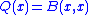 is real-valued only if B is Hermitian, that is, if B(x, y) is always the complex conjugate
is real-valued only if B is Hermitian, that is, if B(x, y) is always the complex conjugate
of B(y, x).
A self-adjoint operator
A on an inner product space
is positive definite if
> 0 for every nonzero vector x.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a definite bilinear form is a bilinear form B over some vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V (with real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
) such that the associated quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....

is definite
Definite quadratic form
In mathematics, a definite quadratic form is a real-valued quadratic form over some vector space V that has the same sign for every nonzero vector of V...
, that is, has a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
value with the same sign
Sign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
(positive or negative) for all non-zero x. According to that sign, B is called positive definite or negative definite. If Q takes both positive and negative values, the bilinear form B is called indefinite.
If B(x, x) ≥ 0 for all x, B is said to be positive semidefinite. Negative semidefinite bilinear forms are defined similarly.
Example
As an example, let V=R2, and consider the bilinear form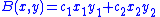
where
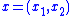 ,
, 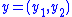 , and
, and 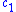 and
and 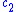 are constants. If
are constants. If 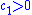 and
and  , the bilinear form
, the bilinear form  is positive definite. If one of the constants is positive and the other is zero, then
is positive definite. If one of the constants is positive and the other is zero, then  is positive semidefinite. If
is positive semidefinite. If 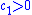 and
and  , then
, then  is indefinite.
is indefinite.Properties
When the scalar field of V is the complex numbers, the function Q defined by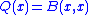 is real-valued only if B is Hermitian, that is, if B(x, y) is always the complex conjugate
is real-valued only if B is Hermitian, that is, if B(x, y) is always the complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of B(y, x).
A self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
A on an inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
is positive definite if
> 0 for every nonzero vector x.
See also
- Positive definite function
- Positive definite matrix

