
Paradoxes of set theory
Encyclopedia
This article contains a discussion of paradoxes of set theory. As with most mathematical paradox
es, they generally reveal surprising and counter-intuitive mathematical results, rather than actual logical contradiction
s within modern axiomatic set theory.
as conceived by Georg Cantor
assumes the existence of infinite sets. As this assumption cannot be proved from first principles it has been introduced into axiomatic set theory by the axiom of infinity
, which asserts the existence of the set N of natural numbers. Every infinite set which can be enumerated by natural numbers is the same size (cardinality) as N, and is said to be countable. Examples of countably infinite sets are the natural numbers, the even numbers, the prime number
s, and also all the rational number
s, i.e., the fractions. These sets have in common the cardinal number
|N| =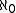 (aleph-nought), a number greater than every natural number.
(aleph-nought), a number greater than every natural number.
Cardinal numbers can be defined as follows. Define two sets to have the same size by: there exists a bijection
between the two sets (a one-to-one correspondence between the elements). Then a cardinal number is, by definition, a class consisting of all sets of the same size. To have the same size is an equivalence relation
, and the cardinal numbers are the equivalence classes.
. For instance, 3 is the ordinal number of the set {0, 1, 2} with the usual order 0 < 1 < 2; and ω is the ordinal number of the set of all natural numbers ordered the usual way. Neglecting the order, we are left with the cardinal number |N| = |ω| =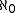 .
.
Ordinal numbers can be defined with the same method used for cardinal numbers. Define two well-ordered sets to have the same order type by: there exists a bijection
between the two sets respecting the order: smaller elements are mapped to smaller elements. Then an ordinal number is, by definition, a class consisting of all well-ordered sets of the same order type. To have the same order type is an equivalence relation
on the class of well-ordered sets, and the ordinal numbers are the equivalence classes.
Two sets of the same order type have the same cardinality. The converse is not true in general for infinite sets: it is possible to impose different well-orderings on the set of natural numbers that give rise to different ordinal numbers.
There is a natural ordering on the ordinals, which is itself a well-ordering. Given any ordinal α, one can consider the set of all ordinals less than α. This set turns out to have ordinal number α. This observation is used for a different way of introducing the ordinals, in which an ordinal is equated with the set of all smaller ordinals. This form of ordinal number is thus a canonical representative of the earlier form of equivalence class.
s of a set S (all possible choices of its elements), we obtain the power set P(S). Georg Cantor proved that the power set is always larger than the set, i.e., |P(S)| > |S|. A special case of Cantor's theorem proves that the set of all real numbers R cannot be enumerated by natural numbers. R is uncountable: |R| > |N|.
and Bernard Bolzano
, among others. Are there as many natural numbers as squares of natural numbers when measured by the method of enumeration?
By defining the notion of the size of a set in terms of its cardinality, the issue can be settled. Since there is a bijection
between the two sets involved, this follows in fact directly from the definition of the cardinality of a set.
See Hilbert's paradox of the Grand Hotel
for more on paradoxes of enumeration.
, after proving that the set of points of a square has the same cardinality as that of the points on just a side of the square: the cardinality of the continuum
.
This demonstrates that the "size" of sets as defined by cardinality alone is not the only useful way of comparing sets. Measure theory provides a more nuanced theory of size that conforms to our intuition that length and area are incompatible measures of size.
proved by means of the axiom of choice (which was introduced for this reason) that every set can be well-ordered. In 1963 Paul J. Cohen showed that using the axiom of choice is essential to well-ordering the real numbers; no weaker assumption suffices.
However, the ability to well order any set allows certain constructions to be performed that have been called paradoxical. One example is the Banach–Tarski paradox
, a theorem widely considered to be nonintuitive. It states that it is possible to decompose a ball of a fixed radius into a finite number of pieces and then move and reassemble those pieces by ordinary translations and rotations
(with no scaling) to obtain two copies from the one original copy. The construction of these pieces requires the axiom of choice; the pieces are not simple regions of the ball, but complicated subsets
.
s) is said to already exist, "by fiat", as an assumption or an axiom. Given this infinite set, other infinite sets are then proven to exist as well, as a logical consequence. But it is still a natural philosophical question to contemplate some physical action that actually completes after an infinite number of discrete steps; and the interpretation of this question using set theory gives rise to the paradoxes of the supertask.
, writes his autobiography so conscientiously that it takes him one year to lay down the events of one day. If he is mortal he can never terminate; but if he lived forever then no part of his diary would remain unwritten, for to each day of his life a year devoted to that day's description would correspond.
The paradox is further increased by the significance of the removal sequence. If the balls are not removed in the sequence 1, 2, 3, ... but in the sequence 1, 11, 21, ... after one hour infinitely many balls populate the reservoir, although the same amount of material as before has been moved.
. The discovery of these paradoxes revealed that not all sets which can be described in the language of naive set theory can actually be said to exist without creating a contradiction. The 20th century saw a resolution to these paradoxes in the development of the various axiomatizations of set theories such as ZFC and NBG
in common use today. However, the gap between the very formalized and symbolic language of these theories and our typical informal use of mathematical language results in various paradoxical situations, as well as the philosophical question of exactly what it is that such formal system
s actually propose to be talking about.
discovered that there is no set containing all ordinal numbers. As every ordinal number is defined by a set of smaller ordinal numbers, the well-ordered set of all ordinal numbers should define an ordinal number Ω which does not belong to the set. On the other hand, Ω must belong to the set of all ordinal numbers. Therefore, the set of all ordinal numbers cannot exist.
By the end of the 19th century Cantor was aware of the non-existence of the set of all cardinal numbers and the set of all ordinal numbers. In letters to David Hilbert
and Richard Dedekind
he wrote about inconsistent sets, the elements of which cannot be thought of as being all together, and he used this result to prove that every consistent set has a cardinal number.
After all this, the version of the "set of all sets" paradox conceived by Bertrand Russell
in 1903 led to a serious crisis in set theory. Russell recognized that the statement x = x is true for every set, and thus the set of all sets is defined by {x | x = x}. In 1906 he constructed several paradox sets, the most famous of which is the set of all sets which do not contain themselves. Russell himself explained this abstract idea by means of some very concrete pictures. One example, known as the Barber paradox
, states: The male barber who shaves all and only men who don't shave themselves has to shave himself only if he does not shave himself.
There are close similarities between Russell's paradox in set theory and the Grelling–Nelson paradox, which demonstrates a paradox in natural language.
published a paradox based on the fact that there are only countably many finite definitions. If we imagine the real numbers as a well-ordered set, those real numbers which can be finitely defined form a subset. Hence in this well-order there should be a first real number that is not finitely definable. This is paradoxical, because this real number has just been finitely defined by the last sentence. This leads to a contradiction in naive set theory
.
This paradox is avoided in axiomatic set theory. Although it is possible to represent a proposition about a set as a set, by a system of codes known as Gödel number
s, there is no formula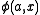 in the language of set theory which holds exactly when a is a code for a finite description of a set and this description is a true description of the set x. This result is known as Tarski's indefinability theorem
in the language of set theory which holds exactly when a is a code for a finite description of a set and this description is a true description of the set x. This result is known as Tarski's indefinability theorem
; it applies to a wide class of formal systems including all commonly studied axiomatizations of set theory.
used a variant of Cantor's diagonal method
to obtain another contradiction in naive set theory. Consider the set A of all finite agglomerations of words. The set E of all finite definitions of real numbers is a subset of A. As A is countable, so is E. Let p be the nth decimal of the nth real number defined by the set E; we form a number N having zero for the integral part and p + 1 for the nth decimal if p is not equal either to 8 or 9, and unity if p is equal to 8 or 9. This number N is not defined by the set E because it differs from any finitely defined real number, namely from the nth number by the nth digit. But N has been defined by a finite number of words in this paragraph. It should therefore be in the set E. That is a contradiction.
As with König's paradox, this paradox cannot be formalized in axiomatic set theory because it requires the ability to tell whether a description applies to a particular set (or, equivalently, to tell whether a formula is actually the definition of a single set).
(1915) the Norwegian logician Thoralf Skolem
showed in 1922 that every consistent theory of first-order predicate calculus, such as set theory, has an at most countable model
. However, Cantor's theorem
proves that there are uncountable sets. The root of this seeming paradox is that the countability or noncountability of a set is not always absolute
, but can depend on the model in which the cardinality is measured. It is possible for a set to be uncountable in one model of set theory but countable in a larger model (because the bijections that establish countability are in the larger model but not the smaller one).
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
es, they generally reveal surprising and counter-intuitive mathematical results, rather than actual logical contradiction
Contradiction
In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other...
s within modern axiomatic set theory.
Cardinal numbers
Set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
as conceived by Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
assumes the existence of infinite sets. As this assumption cannot be proved from first principles it has been introduced into axiomatic set theory by the axiom of infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
, which asserts the existence of the set N of natural numbers. Every infinite set which can be enumerated by natural numbers is the same size (cardinality) as N, and is said to be countable. Examples of countably infinite sets are the natural numbers, the even numbers, the prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s, and also all the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, i.e., the fractions. These sets have in common the cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
|N| =
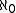 (aleph-nought), a number greater than every natural number.
(aleph-nought), a number greater than every natural number.Cardinal numbers can be defined as follows. Define two sets to have the same size by: there exists a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the two sets (a one-to-one correspondence between the elements). Then a cardinal number is, by definition, a class consisting of all sets of the same size. To have the same size is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, and the cardinal numbers are the equivalence classes.
Ordinal numbers
Besides the cardinality, which describes the size of a set, ordered sets also form a subject of set theory. The axiom of choice guarantees that every set can be well-ordered, which means that a total order can be imposed on its elements such that every nonempty subset has a first element with respect to that order. The order of a well-ordered set is described by an ordinal numberOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
. For instance, 3 is the ordinal number of the set {0, 1, 2} with the usual order 0 < 1 < 2; and ω is the ordinal number of the set of all natural numbers ordered the usual way. Neglecting the order, we are left with the cardinal number |N| = |ω| =
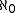 .
.Ordinal numbers can be defined with the same method used for cardinal numbers. Define two well-ordered sets to have the same order type by: there exists a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the two sets respecting the order: smaller elements are mapped to smaller elements. Then an ordinal number is, by definition, a class consisting of all well-ordered sets of the same order type. To have the same order type is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the class of well-ordered sets, and the ordinal numbers are the equivalence classes.
Two sets of the same order type have the same cardinality. The converse is not true in general for infinite sets: it is possible to impose different well-orderings on the set of natural numbers that give rise to different ordinal numbers.
There is a natural ordering on the ordinals, which is itself a well-ordering. Given any ordinal α, one can consider the set of all ordinals less than α. This set turns out to have ordinal number α. This observation is used for a different way of introducing the ordinals, in which an ordinal is equated with the set of all smaller ordinals. This form of ordinal number is thus a canonical representative of the earlier form of equivalence class.
Power sets
By forming all subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of a set S (all possible choices of its elements), we obtain the power set P(S). Georg Cantor proved that the power set is always larger than the set, i.e., |P(S)| > |S|. A special case of Cantor's theorem proves that the set of all real numbers R cannot be enumerated by natural numbers. R is uncountable: |R| > |N|.
Paradoxes of the infinite set
Instead of relying on ambiguous descriptions such as "that which cannot be enlarged" or "increasing without bound", set theory provides definitions for the term infinite set to give an unambiguous meaning to phrases such as "the set of all natural numbers is infinite". Just as for finite sets, the theory makes further definitions which allow us to consistently compare two infinite sets as regards whether one set is "larger than", "smaller than", or "the same size as" the other. But not every intuition regarding the size of finite sets applies to the size of infinite sets, leading to various apparently paradoxical results regarding enumeration, size, measure and order.Paradoxes of enumeration
Before set theory was introduced, the notion of the size of a set had been problematic. It had been discussed by Galileo GalileiGalileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
and Bernard Bolzano
Bernard Bolzano
Bernhard Placidus Johann Nepomuk Bolzano , Bernard Bolzano in English, was a Bohemian mathematician, logician, philosopher, theologian, Catholic priest and antimilitarist of German mother tongue.-Family:Bolzano was the son of two pious Catholics...
, among others. Are there as many natural numbers as squares of natural numbers when measured by the method of enumeration?
- The answer is yes, because for every natural number n there is a square number n2, and likewise the other way around.
- The answer is no, because the squares are a proper subset of the naturals: every square is a natural number but there are natural numbers, like 2, which are not squares of natural numbers.
By defining the notion of the size of a set in terms of its cardinality, the issue can be settled. Since there is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the two sets involved, this follows in fact directly from the definition of the cardinality of a set.
See Hilbert's paradox of the Grand Hotel
Hilbert's paradox of the Grand Hotel
Hilbert's paradox of the Grand Hotel is a mathematical veridical paradox about infinite sets presented by German mathematician David Hilbert .-The paradox:...
for more on paradoxes of enumeration.
Je le vois, mais je ne crois pas
"I see it but I can't believe it", Cantor wrote to Richard DedekindRichard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
, after proving that the set of points of a square has the same cardinality as that of the points on just a side of the square: the cardinality of the continuum
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
.
This demonstrates that the "size" of sets as defined by cardinality alone is not the only useful way of comparing sets. Measure theory provides a more nuanced theory of size that conforms to our intuition that length and area are incompatible measures of size.
Paradoxes of well-ordering
In 1904 Ernst ZermeloErnst Zermelo
Ernst Friedrich Ferdinand Zermelo was a German mathematician, whose work has major implications for the foundations of mathematics and hence on philosophy. He is known for his role in developing Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem.-Life:He graduated...
proved by means of the axiom of choice (which was introduced for this reason) that every set can be well-ordered. In 1963 Paul J. Cohen showed that using the axiom of choice is essential to well-ordering the real numbers; no weaker assumption suffices.
However, the ability to well order any set allows certain constructions to be performed that have been called paradoxical. One example is the Banach–Tarski paradox
Banach–Tarski paradox
The Banach–Tarski paradox is a theorem in set theoretic geometry which states the following: Given a solid ball in 3-dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces , which can then be put back together in a different way to yield two...
, a theorem widely considered to be nonintuitive. It states that it is possible to decompose a ball of a fixed radius into a finite number of pieces and then move and reassemble those pieces by ordinary translations and rotations
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
(with no scaling) to obtain two copies from the one original copy. The construction of these pieces requires the axiom of choice; the pieces are not simple regions of the ball, but complicated subsets
Non-measurable set
In mathematics, a non-measurable set is a set whose structure is so complicated that it cannot be assigned any meaningful measure. Such sets are constructed to shed light on the notions of length, area and volume in formal set theory....
.
Paradoxes of the Supertask
In set theory, an infinite set is not considered to be created by some mathematical process such as "adding one element" that is then carried out "an infinite number of times". Instead, a particular infinite set (such as the set of all natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s) is said to already exist, "by fiat", as an assumption or an axiom. Given this infinite set, other infinite sets are then proven to exist as well, as a logical consequence. But it is still a natural philosophical question to contemplate some physical action that actually completes after an infinite number of discrete steps; and the interpretation of this question using set theory gives rise to the paradoxes of the supertask.
The diary of Tristram Shandy
Tristram Shandy, the hero of a novel by Laurence SterneLaurence Sterne
Laurence Sterne was an Irish novelist and an Anglican clergyman. He is best known for his novels The Life and Opinions of Tristram Shandy, Gentleman, and A Sentimental Journey Through France and Italy; but he also published many sermons, wrote memoirs, and was involved in local politics...
, writes his autobiography so conscientiously that it takes him one year to lay down the events of one day. If he is mortal he can never terminate; but if he lived forever then no part of his diary would remain unwritten, for to each day of his life a year devoted to that day's description would correspond.
The Ross-Littlewood paradox
An increased version of this type of paradox shifts the infinitely remote finish to a finite time. Fill a huge reservoir with balls enumerated by numbers 1 to 10 and take off ball number 1. Then add the balls enumerated by numbers 11 to 20 and take off number 2. Continue to add balls enumerated by numbers 10n - 9 to 10n and to remove ball number n for all natural numbers n = 3, 4, 5, .... Let the first transaction last half an hour, let the second transaction last quarter an hour, and so on, so that all transactions are finished after one hour. Obviously the set of balls in the reservoir increases without bound. Nevertheless, after one hour the reservoir is empty because for every ball the time of removal is known.The paradox is further increased by the significance of the removal sequence. If the balls are not removed in the sequence 1, 2, 3, ... but in the sequence 1, 11, 21, ... after one hour infinitely many balls populate the reservoir, although the same amount of material as before has been moved.
Paradoxes of proof and definability
For all its usefulness in resolving questions regarding infinite sets, naive set theory has some fatal flaws. In particular, it is prey to logical paradoxes such as those exposed by Russell's paradoxRussell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
. The discovery of these paradoxes revealed that not all sets which can be described in the language of naive set theory can actually be said to exist without creating a contradiction. The 20th century saw a resolution to these paradoxes in the development of the various axiomatizations of set theories such as ZFC and NBG
Von Neumann–Bernays–Gödel set theory
In the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
in common use today. However, the gap between the very formalized and symbolic language of these theories and our typical informal use of mathematical language results in various paradoxical situations, as well as the philosophical question of exactly what it is that such formal system
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
s actually propose to be talking about.
Early paradoxes: the set of all sets
In 1897 the Italian mathematician Cesare Burali-FortiCesare Burali-Forti
Cesare Burali-Forti was an Italian mathematician.He was born in Arezzo, and was an assistant of Giuseppe Peano in Turin from 1894 to 1896, during which time he discovered what came to be called the Burali-Forti paradox of Cantorian set theory. He died in Turin.-Books by C. Burali-Forti:* with R....
discovered that there is no set containing all ordinal numbers. As every ordinal number is defined by a set of smaller ordinal numbers, the well-ordered set of all ordinal numbers should define an ordinal number Ω which does not belong to the set. On the other hand, Ω must belong to the set of all ordinal numbers. Therefore, the set of all ordinal numbers cannot exist.
By the end of the 19th century Cantor was aware of the non-existence of the set of all cardinal numbers and the set of all ordinal numbers. In letters to David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
and Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
he wrote about inconsistent sets, the elements of which cannot be thought of as being all together, and he used this result to prove that every consistent set has a cardinal number.
After all this, the version of the "set of all sets" paradox conceived by Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
in 1903 led to a serious crisis in set theory. Russell recognized that the statement x = x is true for every set, and thus the set of all sets is defined by {x | x = x}. In 1906 he constructed several paradox sets, the most famous of which is the set of all sets which do not contain themselves. Russell himself explained this abstract idea by means of some very concrete pictures. One example, known as the Barber paradox
Barber paradox
The Barber paradox is a puzzle derived from Russell's paradox. It was used by Bertrand Russell himself as an illustration of the paradox, though he attributes it to an unnamed person who suggested it to him. It shows that an apparently plausible scenario is logically impossible.- The Paradox...
, states: The male barber who shaves all and only men who don't shave themselves has to shave himself only if he does not shave himself.
There are close similarities between Russell's paradox in set theory and the Grelling–Nelson paradox, which demonstrates a paradox in natural language.
König's paradox
In 1905, the Hungarian mathematician Julius KönigJulius König
Gyula Kőnig was a Hungarian mathematician. He was born in Győr, Hungary and died in Budapest. His mathematical publications in foreign languages appeared under the name Julius König...
published a paradox based on the fact that there are only countably many finite definitions. If we imagine the real numbers as a well-ordered set, those real numbers which can be finitely defined form a subset. Hence in this well-order there should be a first real number that is not finitely definable. This is paradoxical, because this real number has just been finitely defined by the last sentence. This leads to a contradiction in naive set theory
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
.
This paradox is avoided in axiomatic set theory. Although it is possible to represent a proposition about a set as a set, by a system of codes known as Gödel number
Gödel number
In mathematical logic, a Gödel numbering is a function that assigns to each symbol and well-formed formula of some formal language a unique natural number, called its Gödel number. The concept was famously used by Kurt Gödel for the proof of his incompleteness theorems...
s, there is no formula
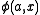 in the language of set theory which holds exactly when a is a code for a finite description of a set and this description is a true description of the set x. This result is known as Tarski's indefinability theorem
in the language of set theory which holds exactly when a is a code for a finite description of a set and this description is a true description of the set x. This result is known as Tarski's indefinability theoremTarski's indefinability theorem
Tarski's undefinability theorem, stated and proved by Alfred Tarski in 1936, is an important limitative result in mathematical logic, the foundations of mathematics, and in formal semantics...
; it applies to a wide class of formal systems including all commonly studied axiomatizations of set theory.
Richard's paradox
In the same year the French mathematician Jules RichardJules Richard
Jules Richard was a French mathematician.- Life and Works:...
used a variant of Cantor's diagonal method
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
to obtain another contradiction in naive set theory. Consider the set A of all finite agglomerations of words. The set E of all finite definitions of real numbers is a subset of A. As A is countable, so is E. Let p be the nth decimal of the nth real number defined by the set E; we form a number N having zero for the integral part and p + 1 for the nth decimal if p is not equal either to 8 or 9, and unity if p is equal to 8 or 9. This number N is not defined by the set E because it differs from any finitely defined real number, namely from the nth number by the nth digit. But N has been defined by a finite number of words in this paragraph. It should therefore be in the set E. That is a contradiction.
As with König's paradox, this paradox cannot be formalized in axiomatic set theory because it requires the ability to tell whether a description applies to a particular set (or, equivalently, to tell whether a formula is actually the definition of a single set).
Paradox of Löwenheim and Skolem
Based upon work of the German mathematician Leopold LöwenheimLeopold Löwenheim
Leopold Löwenheim was a German mathematician, known for his work in mathematical logic. The Nazi regime forced him to retire because under the Nuremberg Laws he was considered only three quarters Aryan. In 1943 much of his work was destroyed during a bombing raid on Berlin...
(1915) the Norwegian logician Thoralf Skolem
Thoralf Skolem
Thoralf Albert Skolem was a Norwegian mathematician known mainly for his work on mathematical logic and set theory.-Life:...
showed in 1922 that every consistent theory of first-order predicate calculus, such as set theory, has an at most countable model
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
. However, Cantor's theorem
Cantor's theorem
In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...
proves that there are uncountable sets. The root of this seeming paradox is that the countability or noncountability of a set is not always absolute
Absoluteness (mathematical logic)
In mathematical logic, a formula is said to be absolute if it has the same truth value in each of some class of structures . Theorems about absoluteness typically establish relationships between the absoluteness of formulas and their syntactic form.There are two weaker forms of partial absoluteness...
, but can depend on the model in which the cardinality is measured. It is possible for a set to be uncountable in one model of set theory but countable in a larger model (because the bijections that establish countability are in the larger model but not the smaller one).

