Absoluteness (mathematical logic)
Encyclopedia
In mathematical logic
, a formula is said to be absolute if it has the same truth value in each of some class of structures
(also called models). Theorems about absoluteness typically establish relationships between the absoluteness of formulas and their syntactic form.
There are two weaker forms of partial absoluteness. If the truth of a formula in each substructure
N of a structure M follows from its truth in M, the formula is downward absolute. If the truth of a formula in a structure N implies its truth in each structure M extending N, the formula is upward absolute.
Issues of absoluteness are particularly important in set theory
and model theory
, fields where multiple structures are considered simultaneously. In model theory, several basic results and definitions are motivated by absoluteness. In set theory, the issue of which properties of sets are absolute is well studied. The Shoenfield absoluteness theorem, due to Joseph Shoenfield (1961), establishes the absoluteness of a large class of formulas between a model of set theory and its constructible universe
, with important methodological consequences. The absoluteness of large cardinal axioms is also studied, with positive and negative results known.
, there are several general results and definitions related to absoluteness. A fundamental example of downward absoluteness is that universal sentences (those with only universal quantifiers) that are true in a structure are also true in every substructure of the original structure. Conversely, existential sentences are upward absolute from a structure to any structure containing it.
Two structures are defined to be elementarily equivalent if they agree about the truth value of all sentences in their shared language, that is, if all sentences in their language are absolute between the two structures. A theory is defined to be model complete if whenever M and N are models of the theory and M is a submodel of N, then M and N are elementarily equivalent.
involves the study of different models of ZF and ZFC. It is crucial for the study of such models to know which properties of a set are absolute to different models. It is common to begin with a fixed model of set theory and only consider other transitive
models containing the same ordinals as the fixed model.
Certain properties are absolute to all transitive models of set theory, including the following (see Jech (2003 sec. I.12) and Kunen (1980 sec. IV.3)).
Other properties, such as countability, are not absolute.
is that although it is a theorem of ZF that the set of real numbers is uncountable, it is consistent that there are countable models of ZF, and the set of real numbers in such a model will be a countable set. The paradox can be resolved by noting that countability is not absolute to submodels of a particular model of ZF. It is possible that a set X is countable in a model of set theory but uncountable in a submodel containing X, because the submodel may contain no bijection between X and ω, while the definition of countability is the existence of such a bijection. The Löwenheim-Skolem theorem, when applied to ZF, shows that this situation does occur.
and 
sentences in the analytical hierarchy
are absolute between a model V of ZFC and the constructible universe
L of the model, when interpreted as statements about the natural numbers in each model. The theorem can be relativized to allow the sentence to use sets of natural numbers from V as parameters, in which case L must be replaced by the smallest submodel containing those parameters and all the ordinals. The theorem has corollaries that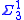
sentences are upward absolute (if such a sentence holds in L then it holds in V) and 
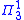sentences are downward absolute (if they hold in V then they hold in L). Because any two transitive models of set theory with the same ordinals have the same constructible universe, Shoenfield's theorem shows that two such models must agree about the truth of all 
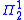sentences.
One consequence of Shoenfield's theorem relates to the axiom of choice. Gödel proved that the constructible universe L always satisfies ZFC, including the axiom of choice, even when V is only assumed to satisfy ZF. Shoenfield's theorem shows that if there is a model ZF in which a given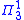
statement φ is false, then φ is also false in the constructible universe of that model. In contrapositive, this means that if ZFC proves a 
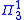sentence then that sentence is also provable in ZF. The same argument can be applied to any other principle which always holds in the constructible universe, such as the combinatorial principle ◊. Even if these principles are independent of ZF, each of their 
consequences is already provable in ZF. In particular, this includes any of their consequences that can be expressed in the language of Peano arithmetic.
Shoenfield's theorem also shows that there are limits to the independence results that can be obtained by forcing
. In particular, any sentence of Peano arithmetic is absolute to transitive models of set theory with the same ordinals. Thus it is not possible to use forcing to change the truth value of arithmetical sentences, as forcing does not change the ordinals of the model to which it is applied. Many famous open problems, such as the Riemann hypothesis
and the P = NP problem, can be expressed as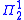
sentences (or sentences of lower complexity), and thus cannot be proven independent of ZFC by forcing.
(L) of any model of set theory. Nevertheless, the constructible universe contains all the ordinal numbers that the original model of set theory contains. This "paradox" can be resolved by noting that the defining properties of some large cardinals are not absolute to submodels.
One example of such a nonabsolute large cardinal axiom is for measurable cardinal
s; for an ordinal to be a measurable cardinal there must exist another set (the measure) satisfying certain properties. It can be shown that no such measure is constructible.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a formula is said to be absolute if it has the same truth value in each of some class of structures
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
(also called models). Theorems about absoluteness typically establish relationships between the absoluteness of formulas and their syntactic form.
There are two weaker forms of partial absoluteness. If the truth of a formula in each substructure
Substructure
In mathematical logic, an substructure or subalgebra is a structure whose domain is a subset of that of a bigger structure, and whose functions and relations are the traces of the functions and relations of the bigger structure...
N of a structure M follows from its truth in M, the formula is downward absolute. If the truth of a formula in a structure N implies its truth in each structure M extending N, the formula is upward absolute.
Issues of absoluteness are particularly important in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
and model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, fields where multiple structures are considered simultaneously. In model theory, several basic results and definitions are motivated by absoluteness. In set theory, the issue of which properties of sets are absolute is well studied. The Shoenfield absoluteness theorem, due to Joseph Shoenfield (1961), establishes the absoluteness of a large class of formulas between a model of set theory and its constructible universe
Constructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
, with important methodological consequences. The absoluteness of large cardinal axioms is also studied, with positive and negative results known.
In model theory
In model theoryModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, there are several general results and definitions related to absoluteness. A fundamental example of downward absoluteness is that universal sentences (those with only universal quantifiers) that are true in a structure are also true in every substructure of the original structure. Conversely, existential sentences are upward absolute from a structure to any structure containing it.
Two structures are defined to be elementarily equivalent if they agree about the truth value of all sentences in their shared language, that is, if all sentences in their language are absolute between the two structures. A theory is defined to be model complete if whenever M and N are models of the theory and M is a submodel of N, then M and N are elementarily equivalent.
In set theory
A major part of modern set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
involves the study of different models of ZF and ZFC. It is crucial for the study of such models to know which properties of a set are absolute to different models. It is common to begin with a fixed model of set theory and only consider other transitive
Transitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
models containing the same ordinals as the fixed model.
Certain properties are absolute to all transitive models of set theory, including the following (see Jech (2003 sec. I.12) and Kunen (1980 sec. IV.3)).
- x is the empty set.
- x is an ordinal.
- X is a finite ordinal.
- x = ω.
- x is (the graph of) a function.
Other properties, such as countability, are not absolute.
Failure of absoluteness for countability
Skolem's paradoxSkolem's paradox
In mathematical logic and philosophy, Skolem's paradox is a seeming contradiction that arises from the downward Löwenheim–Skolem theorem. Thoralf Skolem was the first to discuss the seemingly contradictory aspects of the theorem, and to discover the relativity of set-theoretic notions now known as...
is that although it is a theorem of ZF that the set of real numbers is uncountable, it is consistent that there are countable models of ZF, and the set of real numbers in such a model will be a countable set. The paradox can be resolved by noting that countability is not absolute to submodels of a particular model of ZF. It is possible that a set X is countable in a model of set theory but uncountable in a submodel containing X, because the submodel may contain no bijection between X and ω, while the definition of countability is the existence of such a bijection. The Löwenheim-Skolem theorem, when applied to ZF, shows that this situation does occur.
Shoenfield's absoluteness theorem
Shoenfield's absoluteness theorem shows that and sentences in the analytical hierarchyAnalytical hierarchy
In mathematical logic and descriptive set theory, the analytical hierarchy is a higher type analogue of the arithmetical hierarchy. It thus continues the classification of sets by the formulas that define them.-The analytical hierarchy of formulas:...
are absolute between a model V of ZFC and the constructible universe
Constructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
L of the model, when interpreted as statements about the natural numbers in each model. The theorem can be relativized to allow the sentence to use sets of natural numbers from V as parameters, in which case L must be replaced by the smallest submodel containing those parameters and all the ordinals. The theorem has corollaries that
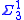sentences are upward absolute (if such a sentence holds in L then it holds in V) and 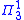sentences are downward absolute (if they hold in V then they hold in L). Because any two transitive models of set theory with the same ordinals have the same constructible universe, Shoenfield's theorem shows that two such models must agree about the truth of all 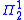sentences.One consequence of Shoenfield's theorem relates to the axiom of choice. Gödel proved that the constructible universe L always satisfies ZFC, including the axiom of choice, even when V is only assumed to satisfy ZF. Shoenfield's theorem shows that if there is a model ZF in which a given
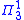statement φ is false, then φ is also false in the constructible universe of that model. In contrapositive, this means that if ZFC proves a 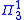sentence then that sentence is also provable in ZF. The same argument can be applied to any other principle which always holds in the constructible universe, such as the combinatorial principle ◊. Even if these principles are independent of ZF, each of their consequences is already provable in ZF. In particular, this includes any of their consequences that can be expressed in the language of Peano arithmetic.Shoenfield's theorem also shows that there are limits to the independence results that can be obtained by forcing
Forcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
. In particular, any sentence of Peano arithmetic is absolute to transitive models of set theory with the same ordinals. Thus it is not possible to use forcing to change the truth value of arithmetical sentences, as forcing does not change the ordinals of the model to which it is applied. Many famous open problems, such as the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
and the P = NP problem, can be expressed as
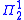sentences (or sentences of lower complexity), and thus cannot be proven independent of ZFC by forcing.Large cardinals
There are certain large cardinals that cannot exist in the constructible universeConstructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
(L) of any model of set theory. Nevertheless, the constructible universe contains all the ordinal numbers that the original model of set theory contains. This "paradox" can be resolved by noting that the defining properties of some large cardinals are not absolute to submodels.
One example of such a nonabsolute large cardinal axiom is for measurable cardinal
Measurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
s; for an ordinal to be a measurable cardinal there must exist another set (the measure) satisfying certain properties. It can be shown that no such measure is constructible.