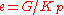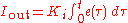
PID controller
Encyclopedia
Controller (control theory)
In control theory, a controller is a device which monitors and affects the operational conditions of a given dynamical system. The operational conditions are typically referred to as output variables of the system which can be affected by adjusting certain input variables...
) widely used in industrial control system
Control system
A control system is a device, or set of devices to manage, command, direct or regulate the behavior of other devices or system.There are two common classes of control systems, with many variations and combinations: logic or sequential controls, and feedback or linear controls...
s – a PID is the most commonly used feedback controller. A PID controller calculates an "error" value as the difference between a measured process variable
Process variable
A process variable, process value or process parameter is the current status of a process under control. An example of this would be the temperature of a furnace. The current temperature is called the process variable, while the desired temperature is known as the set-point.Measurement of process...
and a desired setpoint. The controller attempts to minimize the error by adjusting the process control inputs.
The PID controller calculation (algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
) involves three separate constant parameters, and is accordingly sometimes called three-term control: the proportional
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
, the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
and derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
values, denoted P, I, and D. Heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
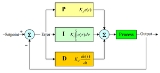
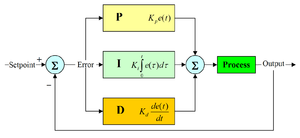
ally, these values can be interpreted in terms of time: P depends on the present error, I on the accumulation of past errors, and D is a prediction of future errors, based on current rate of change. The weighted sum of these three actions is used to adjust the process via a control element such as the position of a control valve, or the power supplied to a heating element.
In the absence of knowledge of the underlying process, a PID controller is the best controller. By tuning the three parameters in the PID controller algorithm, the controller can provide control action designed for specific process requirements. The response of the controller can be described in terms of the responsiveness of the controller to an error, the degree to which the controller overshoots
Overshoot (signal)
In signal processing, control theory, electronics, and mathematics, overshoot is when a signal or function exceeds its target. It arises especially in the step response of bandlimited systems such as low-pass filters...
the setpoint and the degree of system oscillation. Note that the use of the PID algorithm for control does not guarantee optimal control
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
of the system or system stability.
Some applications may require using only one or two actions to provide the appropriate system control. This is achieved by setting the other parameters to zero. A PID controller will be called a PI, PD, P or I controller in the absence of the respective control actions. PI controllers are fairly common, since derivative action is sensitive to measurement noise, whereas the absence of an integral term may prevent the system from reaching its target value due to the control action.
Control loop basics
A familiar example of a control loop is the action taken when adjusting hot and cold faucets (valves) to maintain the water at a desired temperature. This typically involves the mixing of two process streams, the hot and cold water. The person touches the water to sense or measure its temperature. Based on this feedback they perform a control action to adjust the hot and cold water valves until the process temperature stabilizes at the desired value.The sensed water temperature is the process variable
Process variable
A process variable, process value or process parameter is the current status of a process under control. An example of this would be the temperature of a furnace. The current temperature is called the process variable, while the desired temperature is known as the set-point.Measurement of process...
or process value (PV). The desired temperature is called the setpoint (SP). The input to the process (the water valve position) is called the manipulated variable (MV). The difference between the temperature measurement and the set point is the error (e) and quantifies whether the water is too hot or too cold and by how much.
After measuring the temperature (PV), and then calculating the error, the controller decides when to change the tap position (MV) and by how much. When the controller first turns the valve on, it may turn the hot valve only slightly if warm water is desired, or it may open the valve all the way if very hot water is desired. This is an example of a simple proportional control. In the event that hot water does not arrive quickly, the controller may try to speed-up the process by opening up the hot water valve more-and-more as time goes by. This is an example of an integral control.
Making a change that is too large when the error is small is equivalent to a high gain controller and will lead to overshoot. If the controller were to repeatedly make changes that were too large and repeatedly overshoot the target, the output would oscillate around the setpoint in either a constant, growing, or decaying sinusoid. If the oscillations increase with time then the system is unstable, whereas if they decrease the system is stable. If the oscillations remain at a constant magnitude the system is marginally stable
Marginal stability
In the theory of dynamical systems, and control theory, a continuous linear time-invariant system is marginally stable if and only if the real part of every eigenvalue in the system's transfer-function is non-positive, and all eigenvalues with zero real value are simple roots...
.
In the interest of achieving a gradual convergence at the desired temperature (SP), the controller may wish to damp
Damping
In physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect...
the anticipated future oscillations. So in order to compensate for this effect, the controller may elect to temper its adjustments. This can be thought of as a derivative control method.
If a controller starts from a stable state at zero error (PV = SP), then further changes by the controller will be in response to changes in other measured or unmeasured inputs to the process that impact on the process, and hence on the PV. Variables that impact on the process other than the MV are known as disturbances. Generally controllers are used to reject disturbances and/or implement setpoint changes. Changes in feedwater temperature constitute a disturbance to the faucet temperature control process.
In theory, a controller can be used to control any process which has a measurable output (PV), a known ideal value for that output (SP) and an input to the process (MV) that will affect the relevant PV. Controllers are used in industry to regulate temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, flow rate, chemical composition, speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
and practically every other variable for which a measurement exists.
PID controller theory
- This section describes the parallel or non-interacting form of the PID controller. For other forms please see the section Alternative nomenclature and PID forms.
The PID control scheme is named after its three correcting terms, whose sum constitutes the manipulated variable (MV). The proportional, integral, and derivative terms are summed to calculate the output of the PID controller. Defining
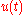 as the controller output, the final form of the PID algorithm is:
as the controller output, the final form of the PID algorithm is: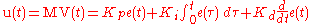
where
-
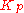 : Proportional gain, a tuning parameter
: Proportional gain, a tuning parameter -
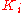 : Integral gain, a tuning parameter
: Integral gain, a tuning parameter -
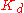 : Derivative gain, a tuning parameter
: Derivative gain, a tuning parameter -
 : Error
: Error 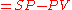
-
 : Time or instantaneous time (the present)
: Time or instantaneous time (the present)
Proportional term
The proportional term is given by:
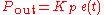
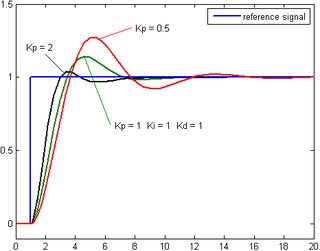
A high proportional gain results in a large change in the output for a given change in the error. If the proportional gain is too high, the system can become unstable (see the section on loop tuning). In contrast, a small gain results in a small output response to a large input error, and a less responsive or less sensitive controller. If the proportional gain is too low, the control action may be too small when responding to system disturbances. Tuning theory and industrial practice indicate that the proportional term should contribute the bulk of the output change.
Droop
A pure proportional controller will not always settle at its target value, but may retain a steady-state error. Specifically, drift in the absence of control, such as cooling of a furnace towards room temperature, biases a pure proportional controller. If the drift is downwards, as in cooling, then the bias will be below the set point, hence the term "droop".Droop is proportional to the process gain and inversely proportional to proportional gain. Specifically the steady-state error is given by:
Droop is an inherent defect of purely proportional control. Droop may be mitigated by adding a compensating bias term (setting the setpoint above the true desired value), or corrected by adding an integral term.
Integral term
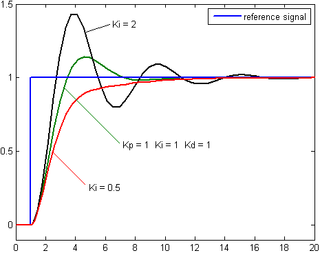
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
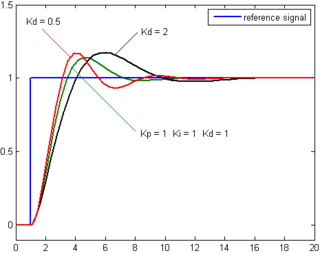
in a PID controller is the sum of the instantaneous error over time and gives the accumulated offset that should have been corrected previously. The accumulated error is then multiplied by the integral gain (
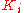 ) and added to the controller output.
) and added to the controller output.The integral term is given by:
The integral term accelerates the movement of the process towards setpoint and eliminates the residual steady-state error that occurs with a pure proportional controller. However, since the integral term responds to accumulated errors from the past, it can cause the present value to overshoot
Overshoot (signal)
In signal processing, control theory, electronics, and mathematics, overshoot is when a signal or function exceeds its target. It arises especially in the step response of bandlimited systems such as low-pass filters...
the setpoint value (see the section on loop tuning).
Derivative term
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the process error is calculated by determining the slope of the error over time and multiplying this rate of change by the derivative gain
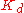 . The magnitude of the contribution of the derivative term to the overall control action is termed the derivative gain,
. The magnitude of the contribution of the derivative term to the overall control action is termed the derivative gain, 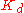 .
.The derivative term is given by:
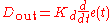
The derivative term slows the rate of change of the controller output. Derivative control is used to reduce the magnitude of the overshoot produced by the integral component and improve the combined controller-process stability. However, the derivative term slows the transient response
Transient response
In electrical engineering and mechanical engineering, a transient response or natural response is the response of a system to a change from equilibrium. The transient response is not necessarily tied to "on/off" events but to any event that affects the equilibrium of the system...
of the controller. Also, differentiation of a signal amplifies noise and thus this term in the controller is highly sensitive to noise in the error term, and can cause a process to become unstable if the noise and the derivative gain are sufficiently large. Hence an approximation to a differentiator with a limited bandwidth is more commonly used. Such a circuit is known as a phase-lead compensator.
Loop tuning
Tuning a control loop is the adjustment of its control parameters (gain/proportional band, integral gain/reset, derivative gain/rate) to the optimum values for the desired control response. Stability (bounded oscillation) is a basic requirement, but beyond that, different systems have different behavior, different applications have different requirements, and requirements may conflict with one another.PID tuning is a difficult problem, even though there are only three parameters and in principle is simple to describe, because it must satisfy complex criteria within the limitations of PID control. There are accordingly various methods for loop tuning, and more sophisticated techniques are the subject of patents; this section describes some traditional manual methods for loop tuning.
Designing and tuning a PID controller appears to be conceptually intuitive, but can be hard in practice, if multiple (and often conflicting) objectives such as short transient and high stability are to be achieved. Usually, initial designs need to be adjusted repeatedly through computer simulations until the closed-loop system performs or compromises as desired.
Some processes have a degree of non-linearity and so parameters that work well at full-load conditions don't work when the process is starting up from no-load; this can be corrected by gain scheduling
Gain scheduling
In control theory, gain scheduling is an approach to control of non-linear systems that uses a family of linear controllers, each of which provides satisfactory control for a different operating point of the system....
(using different parameters in different operating regions). PID controllers often provide acceptable control using default tunings, but performance can generally be improved by careful tuning, and performance may be unacceptable with poor tuning.
Stability
If the PID controller parameters (the gains of the proportional, integral and derivative terms) are chosen incorrectly, the controlled process input can be unstable, i.e. its output divergesDivergence (computer science)
In computer science, a computation is said to diverge if it does not terminate or terminates in an exceptional state. Otherwise it is said to converge...
, with or without oscillation
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
, and is limited only by saturation or mechanical breakage. Instability is caused by excess gain, particularly in the presence of significant lag
Lag
Lag is a common word meaning to fail to keep up or to fall behind. In real-time applications, the term is used when the application fails to respond in a timely fashion to inputs...
.
Generally, stability of response is required and the process must not oscillate for any combination of process conditions and setpoints, though sometimes marginal stability
Marginal stability
In the theory of dynamical systems, and control theory, a continuous linear time-invariant system is marginally stable if and only if the real part of every eigenvalue in the system's transfer-function is non-positive, and all eigenvalues with zero real value are simple roots...
(bounded oscillation) is acceptable or desired.
Optimum behavior
The optimum behavior on a process change or setpoint change varies depending on the application.Two basic requirements are regulation (disturbance rejection – staying at a given setpoint) and command tracking (implementing setpoint changes) – these refer to how well the controlled variable tracks the desired value. Specific criteria for command tracking include rise time
Rise time
In electronics, when describing a voltage or current step function, rise time refers to the time required for a signal to change from a specified low value to a specified high value...
and settling time
Settling time
The settling time of an amplifier or other output device is the time elapsed from the application of an ideal instantaneous step input to the time at which the amplifier output has entered and remained within a specified error band, usually symmetrical about the final value.Settling time includes a...
. Some processes must not allow an overshoot of the process variable beyond the setpoint if, for example, this would be unsafe. Other processes must minimize the energy expended in reaching a new setpoint.
Overview of methods
There are several methods for tuning a PID loop. The most effective methods generally involve the development of some form of process model, then choosing P, I, and D based on the dynamic model parameters. Manual tuning methods can be relatively inefficient, particularly if the loops have response times on the order of minutes or longer.The choice of method will depend largely on whether or not the loop can be taken "offline" for tuning, and the response time of the system. If the system can be taken offline, the best tuning method often involves subjecting the system to a step change in input, measuring the output as a function of time, and using this response to determine the control parameters.
| Method | Advantages | Disadvantages |
|---|---|---|
| Manual Tuning | No math required. Online method. | Requires experienced personnel. |
| Ziegler–Nichols | Proven Method. Online method. | Process upset, some trial-and-error, very aggressive tuning. |
| Software Tools | Consistent tuning. Online or offline method. May include valve and sensor analysis. Allow simulation before downloading. Can support Non-Steady State (NSS) Tuning. | Some cost and training involved. |
| Cohen-Coon | Good process models. | Some math. Offline method. Only good for first-order processes. |
Manual tuning
If the system must remain online, one tuning method is to first set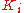 and
and 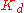 values to zero. Increase the
values to zero. Increase the 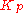 until the output of the loop oscillates, then the
until the output of the loop oscillates, then the 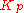 should be set to approximately half of that value for a "quarter amplitude decay" type response. Then increase
should be set to approximately half of that value for a "quarter amplitude decay" type response. Then increase 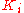 until any offset is corrected in sufficient time for the process. However, too much
until any offset is corrected in sufficient time for the process. However, too much 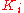 will cause instability. Finally, increase
will cause instability. Finally, increase 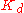 , if required, until the loop is acceptably quick to reach its reference after a load disturbance. However, too much
, if required, until the loop is acceptably quick to reach its reference after a load disturbance. However, too much 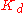 will cause excessive response and overshoot. A fast PID loop tuning usually overshoots slightly to reach the setpoint more quickly; however, some systems cannot accept overshoot, in which case an over-damped closed-loop system is required, which will require a
will cause excessive response and overshoot. A fast PID loop tuning usually overshoots slightly to reach the setpoint more quickly; however, some systems cannot accept overshoot, in which case an over-damped closed-loop system is required, which will require a 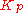 setting significantly less than half that of the
setting significantly less than half that of the 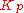 setting causing oscillation.
setting causing oscillation.| Parameter | Rise time | Overshoot | Settling time | Steady-state error | Stability |
|---|---|---|---|---|---|
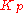 |
Decrease | Increase | Small change | Decrease | Degrade |
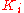 |
Decrease | Increase | Increase | Decrease significantly | Degrade |
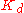 |
Minor decrease | Minor decrease | Minor decrease | No effect in theory | Improve if 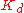 small small |
Ziegler–Nichols method
Another heuristic tuning method is formally known as the Ziegler–Nichols methodZiegler–Nichols method
The Ziegler–Nichols tuning method is a heuristic method of tuning a PID controller. It was developed by John G. Ziegler and Nathaniel B. Nichols. It is performed by setting the I and D gains to zero...
, introduced by John G. Ziegler and Nathaniel B. Nichols
Nathaniel B. Nichols
Nathaniel B. Nichols was an American control engineer who made significant contributions to the field of control theory. He is well-known for his book Theory of Servomechanism, one of the most widely read books in control engineering....
in the 1940s. As in the method above, the
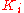 and
and 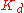 gains are first set to zero. The P gain is increased until it reaches the ultimate gain,
gains are first set to zero. The P gain is increased until it reaches the ultimate gain, 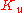 , at which the output of the loop starts to oscillate.
, at which the output of the loop starts to oscillate. 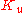 and the oscillation period
and the oscillation period 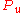 are used to set the gains as shown:
are used to set the gains as shown:| Control Type | 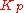 |
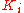 |
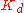 |
|---|---|---|---|
| P | 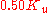 |
- | - |
| PI | 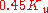 |
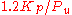 |
- |
| PID | 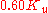 |
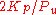 |
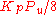 |
These gains apply to the ideal, parallel form of the PID controller. When applied to the standard PID form, the integral and derivative time parameters
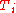 and
and 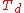 are only dependent on the oscillation period
are only dependent on the oscillation period 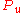 . Please see the section "Alternative nomenclature and PID forms".
. Please see the section "Alternative nomenclature and PID forms".PID tuning software
Most modern industrial facilities no longer tune loops using the manual calculation methods shown above. Instead, PID tuning and loop optimization software are used to ensure consistent results. These software packages will gather the data, develop process models, and suggest optimal tuning. Some software packages can even develop tuning by gathering data from reference changes.Mathematical PID loop tuning induces an impulse in the system, and then uses the controlled system's frequency response to design the PID loop values. In loops with response times of several minutes, mathematical loop tuning is recommended, because trial and error can literally take days just to find a stable set of loop values. Optimal values are harder to find. Some digital loop controllers offer a self-tuning feature in which very small setpoint changes are sent to the process, allowing the controller itself to calculate optimal tuning values.
Other formulas are available to tune the loop according to different performance criteria. Many patented formulas are now embedded within PID tuning software and hardware modules.
Advances in automated PID Loop Tuning software also deliver algorithms for tuning PID Loops in a dynamic or Non-Steady State (NSS) scenario. The software will model the dynamics of a process, through a disturbance, and calculate PID control parameters in response.
Modifications to the PID algorithm
The basic PID algorithm presents some challenges in control applications that have been addressed by minor modifications to the PID form.Integral windup:
One common problem resulting from the ideal PID implementations is integral windup
Integral windup
Integral windup refers to the situation in a PID controller where a large change in setpoint occurs and the integral terms accumulates a significant error during the rise , thus overshooting and continuing to increase as this accumulated error is unwound...
, where a large change in setpoint occurs (say a positive change) and the integral term accumulates an error larger than the maximal value for the regulation variable (windup), thus the system overshoots and continues to increase as this accumulated error is unwound. This problem can be addressed by:
- Initializing the controller integral to a desired value
- Increasing the setpoint in a suitable ramp
- Disabling the integral function until the PV has entered the controllable region
- Limiting the time period over which the integral error is calculated
- Preventing the integral term from accumulating above or below pre-determined bounds
Overshooting from known disturbances: For example, a PID loop is used to control the temperature of an electric resistance furnace, the system has stabilized. Now the door is opened and something cold is put into the furnace the temperature drops below the setpoint. The integral function of the controller tends to compensate this error by introducing another error in the positive direction. This overshoot can be avoided by freezing of the integral function after the opening of the door for the time the control loop typically needs to reheat the furnace.
Replacing the integral function by a model based part: Often the time-response of the system is approximately known. Then it is an advantage to simulate this time-response with a model and to calculate some unknown parameter from the actual response of the system. If for instance the system is an electrical furnace the response of the difference between furnace temperature and ambient temperature to changes of the electrical power will be similar to that of a simple RC low-pass filter multiplied by an unknown proportional coefficient. The actual electrical power supplied to the furnace is delayed by a low-pass filter to simulate the response of the temperature of the furnace and then the actual temperature minus the ambient temperature is divided by this low-pass filtered electrical power. Then, the result is stabilized by another low-pass filter leading to an estimation of the proportional coefficient. With this estimation, it is possible to calculate the required electrical power by dividing the set-point of the temperature minus the ambient temperature by this coefficient. The result can then be used instead of the integral function. This also achieves a control error of zero in the steady-state, but avoids integral windup and can give a significantly improved control action compared to an optimized PID controller. This type of controller does work properly in an open loop situation which causes integral windup with an integral function. This is an advantage if, for example, the heating of a furnace has to be reduced for some time because of the failure of a heating element, or if the controller is used as an advisory system to a human operator who may not switch it to closed-loop operation. It may also be useful if the controller is inside a branch of a complex control system that may be temporarily inactive.
Many PID loops control a mechanical device (for example, a valve). Mechanical maintenance can be a major cost and wear leads to control degradation in the form of either stiction
Stiction
Stiction is the static friction that needs to be overcome to enable relative motion of stationary objects in contact. The term is a portmanteau of the term "static friction", perhaps also influenced by the verb "stick"....
or a deadband
Deadband
A deadband is an area of a signal range or band where no action occurs . Deadband is used in voltage regulators and other controllers...
in the mechanical response to an input signal. The rate of mechanical wear is mainly a function of how often a device is activated to make a change. Where wear is a significant concern, the PID loop may have an output deadband
Deadband
A deadband is an area of a signal range or band where no action occurs . Deadband is used in voltage regulators and other controllers...
to reduce the frequency of activation of the output (valve). This is accomplished by modifying the controller to hold its output steady if the change would be small (within the defined deadband range). The calculated output must leave the deadband before the actual output will change.
The proportional and derivative terms can produce excessive movement in the output when a system is subjected to an instantaneous step increase in the error, such as a large setpoint change. In the case of the derivative term, this is due to taking the derivative of the error, which is very large in the case of an instantaneous step change. As a result, some PID algorithms incorporate the following modifications:
Derivative of the Process Variable: In this case the PID controller measures the derivative of the measured process variable
Process variable
A process variable, process value or process parameter is the current status of a process under control. An example of this would be the temperature of a furnace. The current temperature is called the process variable, while the desired temperature is known as the set-point.Measurement of process...
(PV), rather than the derivative of the error. This quantity is always continuous (i.e., never has a step change as a result of changed setpoint). For this technique to be effective, the derivative of the PV must have the same sign as the derivative of the error.
Setpoint ramping: In this modification, the setpoint is gradually moved from its old value to a newly specified value using a linear or first order differential ramp function. This avoids the discontinuity present in a simple step change.
Setpoint weighting: Setpoint weighting uses different multipliers for the error depending on which element of the controller it is used in. The error in the integral term must be the true control error to avoid steady-state control errors. This affects the controller's setpoint response. These parameters do not affect the response to load disturbances and measurement noise.
History

Russian American
Russian Americans are primarily Americans who traces their ancestry to Russia. The definition can be applied to recent Russian immigrants to the United States, as well as to settlers of 19th century Russian settlements in northwestern America which includes today's California, Alaska and...
engineer Nicolas Minorsky, in . Minorsky was designing automatic steering systems for the US Navy, and based his analysis on observations of a helmsman
Helmsman
A helmsman is a person who steers a ship, sailboat, submarine, or other type of maritime vessel. On small vessels, particularly privately-owned noncommercial vessels, the functions of skipper and helmsman may be combined in one person. On larger vessels, there is a separate officer of the watch,...
, observing that the helmsman controlled the ship not only based on the current error, but also on past error and current rate of change; this was then made mathematical by Minorsky. His goal was stability, not general control, which significantly simplified the problem. While proportional control provides stability against small disturbances, it was insufficient for dealing with a steady disturbance, notably a stiff gale (due to droop), which required adding the integral term. Finally, the derivative term was added to improve control.
Trials were carried out on the USS New Mexico
USS New Mexico (BB-40)
USS New Mexico was a battleship in service with the United States Navy from 1918 to 1946. She was the lead ship of a class of three battleships. New Mexico was extensively modernized between 1931 and 1933 and saw service during World War II both in the Atlantic and Pacific theatres. After her...
, with the controller controlling the angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
(not angle) of the rudder. PI control yielded sustained yaw (angular error) of ±2°, while adding D yielded yaw of ±1/6°, better than most helmsmen could achieve.
The Navy ultimately did not adopt the system, due to resistance by personnel. Similar work was carried out and published by several others in the 1930s.
Limitations of PID control
While PID controllers are applicable to many control problems, and often perform satisfactorily without any improvements or even tuning, they can perform poorly in some applications, and do not in general provide optimal controlOptimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
. The fundamental difficulty with PID control is that it is a feedback system, with constant parameters, and no direct knowledge of the process, and thus overall performance is reactive and a compromise – while PID control is the best controller with no model of the process, better performance can be obtained by incorporating a model of the process.
The most significant improvement is to incorporate feed-forward control with knowledge about the system, and using the PID only to control error. Alternatively, PIDs can be modified in more minor ways, such as by changing the parameters (either gain scheduling
Gain scheduling
In control theory, gain scheduling is an approach to control of non-linear systems that uses a family of linear controllers, each of which provides satisfactory control for a different operating point of the system....
in different use cases or adaptively modifying them based on performance), improving measurement (higher sampling rate, precision, and accuracy, and low-pass filtering if necessary), or cascading multiple PID controllers.
PID controllers, when used alone, can give poor performance when the PID loop gains must be reduced so that the control system does not overshoot, oscillate or hunt about the control setpoint value. They also have difficulties in the presence of non-linearities, may trade-off regulation versus response time, do not react to changing process behavior (say, the process changes after it has warmed up), and have lag in responding to large disturbances.
Linearity
Another problem faced with PID controllers is that they are linear, and in particular symmetric. Thus, performance of PID controllers in non-linear systems (such as HVAC systemsHVAC control system
-Direct digital control:Central controllers and most terminal unit controllers are programmable, meaning the direct digital control program code may be customized for the intended use. The program features include time schedules, setpoints, controllers, logic, timers, trend logs, and alarms...
) is variable. For example, in temperature control, a common use case is active heating (via a heating element) but passive cooling (heating off, but no cooling), so overshoot can only be corrected slowly – it cannot be forced downward. In this case the PID should be tuned to be overdamped, to prevent or reduce overshoot, though this reduces performance (it increases settling time).
Noise in derivative
A problem with the derivative term is that small amounts of measurement or process noiseNoise
In common use, the word noise means any unwanted sound. In both analog and digital electronics, noise is random unwanted perturbation to a wanted signal; it is called noise as a generalisation of the acoustic noise heard when listening to a weak radio transmission with significant electrical noise...
can cause large amounts of change in the output. It is often helpful to filter the measurements with a low-pass filter
Low-pass filter
A low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
in order to remove higher-frequency noise components. However, low-pass filtering and derivative control can cancel each other out, so reducing noise by instrumentation means is a much better choice. Alternatively, a nonlinear median filter
Median filter
In signal processing, it is often desirable to be able to perform some kind of noise reduction on an image or signal. The median filter is a nonlinear digital filtering technique, often used to remove noise. Such noise reduction is a typical pre-processing step to improve the results of later...
may be used, which improves the filtering efficiency and practical performance. In some case, the differential band can be turned off in many systems with little loss of control. This is equivalent to using the PID controller as a PI controller.
Feed-forward
The control system performance can be improved by combining the feedbackFeedback
Feedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
(or closed-loop) control of a PID controller with feed-forward
Feed-forward
Feed-forward is a term describing an element or pathway within a control system which passes a controlling signal from a source in the control system's external environment, often a command signal from an external operator, to a load elsewhere in its external environment...
(or open-loop) control. Knowledge about the system (such as the desired acceleration and inertia) can be fed forward and combined with the PID output to improve the overall system performance. The feed-forward value alone can often provide the major portion of the controller output. The PID controller can be used primarily to respond to whatever difference or error remains between the setpoint (SP) and the actual value of the process variable (PV). Since the feed-forward output is not affected by the process feedback, it can never cause the control system to oscillate, thus improving the system response and stability.
For example, in most motion control systems, in order to accelerate a mechanical load under control, more force or torque is required from the prime mover, motor, or actuator. If a velocity loop PID controller is being used to control the speed of the load and command the force or torque being applied by the prime mover, then it is beneficial to take the instantaneous acceleration desired for the load, scale that value appropriately and add it to the output of the PID velocity loop controller. This means that whenever the load is being accelerated or decelerated, a proportional amount of force is commanded from the prime mover regardless of the feedback value. The PID loop in this situation uses the feedback information to change the combined output to reduce the remaining difference between the process setpoint and the feedback value. Working together, the combined open-loop feed-forward controller and closed-loop PID controller can provide a more responsive, stable and reliable control system.
Other improvements
In addition to feed-forward, PID controllers are often enhanced through methods such as PID gain schedulingGain scheduling
In control theory, gain scheduling is an approach to control of non-linear systems that uses a family of linear controllers, each of which provides satisfactory control for a different operating point of the system....
(changing parameters in different operating conditions), fuzzy logic
Fuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
or computational verb logic.
Further practical application issues can arise from instrumentation connected to the controller. A high enough sampling rate, measurement precision, and measurement accuracy are required to achieve adequate control performance. Another new method for improvement of PID controller is to increase the degree of freedom by using fractional order. The order of the integrator and differentiator add increased flexibility to the controller.
Cascade control
One distinctive advantage of PID controllers is that two PID controllers can be used together to yield better dynamic performance. This is called cascaded PID control. In cascade control there are two PIDs arranged with one PID controlling the set point of another. A PID controller acts as outer loop controller, which controls the primary physical parameter, such as fluid level or velocity. The other controller acts as inner loop controller, which reads the output of outer loop controller as set point, usually controlling a more rapid changing parameter, flowrate or acceleration. It can be mathematically proven that the working frequency of the controller is increased and the time constant of the object is reduced by using cascaded PID controller..Physical implementation of PID control
In the early history of automatic process control the PID controller was implemented as a mechanical device. These mechanical controllers used a leverLever
In physics, a lever is a rigid object that is used with an appropriate fulcrum or pivot point to either multiply the mechanical force that can be applied to another object or resistance force , or multiply the distance and speed at which the opposite end of the rigid object travels.This leverage...
, spring
Spring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...
and a mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
and were often energized by compressed air. These pneumatic controllers were once the industry standard.
Electronic analog controllers can be made from a solid-state
Transistor
A transistor is a semiconductor device used to amplify and switch electronic signals and power. It is composed of a semiconductor material with at least three terminals for connection to an external circuit. A voltage or current applied to one pair of the transistor's terminals changes the current...
or tube
Vacuum tube
In electronics, a vacuum tube, electron tube , or thermionic valve , reduced to simply "tube" or "valve" in everyday parlance, is a device that relies on the flow of electric current through a vacuum...
amplifier
Operational amplifier
An operational amplifier is a DC-coupled high-gain electronic voltage amplifier with a differential input and, usually, a single-ended output...
, a capacitor
Capacitor
A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
and a resistance
Electrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
. Electronic analog PID control loops were often found within more complex electronic systems, for example, the head positioning of a disk drive, the power conditioning of a power supply
Power supply
A power supply is a device that supplies electrical energy to one or more electric loads. The term is most commonly applied to devices that convert one form of electrical energy to another, though it may also refer to devices that convert another form of energy to electrical energy...
, or even the movement-detection circuit of a modern seismometer
Seismometer
Seismometers are instruments that measure motions of the ground, including those of seismic waves generated by earthquakes, volcanic eruptions, and other seismic sources...
. Nowadays, electronic controllers have largely been replaced by digital controllers implemented with microcontrollers or FPGAs.
Most modern PID controllers in industry are implemented in programmable logic controller
Programmable logic controller
A programmable logic controller or programmable controller is a digital computer used for automation of electromechanical processes, such as control of machinery on factory assembly lines, amusement rides, or light fixtures. PLCs are used in many industries and machines...
s (PLCs) or as a panel-mounted digital controller. Software implementations have the advantages that they are relatively cheap and are flexible with respect to the implementation of the PID algorithm.
Variable voltages may be applied by the time proportioning form of Pulse-width modulation
Pulse-width modulation
Pulse-width modulation , or pulse-duration modulation , is a commonly used technique for controlling power to inertial electrical devices, made practical by modern electronic power switches....
(PWM) – a cycle time is fixed, and variation is achieved by varying the proportion of the time during this cycle that the controller outputs +1 (or −1) instead of 0. On a digital system the possible proportions are discrete – e.g., increments of .1 second within a 2 second cycle time yields 20 possible steps: percentage increments of 5% – so there is a discretization error
Discretization error
In numerical analysis, computational physics, and simulation, discretization error is error resulting from the fact that a function of a continuous variable is represented in the computer by a finite number of evaluations, for example, on a lattice...
, but for high enough time resolution this yields satisfactory performance.
Ideal versus standard PID form
The form of the PID controller most often encountered in industry, and the one most relevant to tuning algorithms is the standard form. In this form the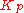 gain is applied to the
gain is applied to the  , and
, and  terms, yielding:
terms, yielding: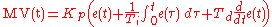
where
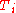 is the integral time
is the integral time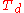 is the derivative time
is the derivative timeIn this standard form, the parameters have a clear physical meaning. In particular, the inner summation produces a new single error value which is compensated for future and past errors. The addition of the proportional and derivative components effectively predicts the error value at
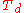 seconds (or samples) in the future, assuming that the loop control remains unchanged. The integral component adjusts the error value to compensate for the sum of all past errors, with the intention of completely eliminating them in
seconds (or samples) in the future, assuming that the loop control remains unchanged. The integral component adjusts the error value to compensate for the sum of all past errors, with the intention of completely eliminating them in 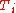 seconds (or samples). The resulting compensated single error value is scaled by the single gain
seconds (or samples). The resulting compensated single error value is scaled by the single gain 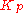 .
.In the ideal parallel form, shown in the controller theory section
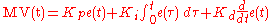
the gain parameters are related to the parameters of the standard form through
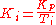 and
and 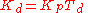 . This parallel form, where the parameters are treated as simple gains, is the most general and flexible form. However, it is also the form where the parameters have the least physical interpretation and is generally reserved for theoretical treatment of the PID controller. The standard form, despite being slightly more complex mathematically, is more common in industry.
. This parallel form, where the parameters are treated as simple gains, is the most general and flexible form. However, it is also the form where the parameters have the least physical interpretation and is generally reserved for theoretical treatment of the PID controller. The standard form, despite being slightly more complex mathematically, is more common in industry.Basing derivative action on PV
In most commercial control systems, derivative action is based on PV rather than error. This is because the digitised version of the algorithm produces a large unwanted spike when the SP is changed. If the SP is constant then changes in PV will be the same as changes in error. Therefore this modification makes no difference to the way the controller responds to process disturbances.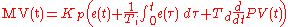
Basing proportional action on PV
Most commercial control systems offer the option of also basing the proportional action on PV. This means that only the integral action responds to changes in SP. While at first this might seem to adversely affect the time that the process will take to respond to the change, the controller may be retuned to give almost the same response - largely by increasing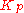 . The modification to the algorithm does not affect the way the controller responds to process disturbances, but the change in tuning has a beneficial effect. Often the magnitude and duration of the disturbance will be more than halved. Since most controllers have to deal frequently with process disturbances and relatively rarely with SP changes, properly tuned the modified algorithm can dramatically improve process performance.
. The modification to the algorithm does not affect the way the controller responds to process disturbances, but the change in tuning has a beneficial effect. Often the magnitude and duration of the disturbance will be more than halved. Since most controllers have to deal frequently with process disturbances and relatively rarely with SP changes, properly tuned the modified algorithm can dramatically improve process performance.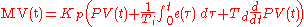
Tuning methods such as Ziegler-Nichols and Cohen-Coon will not be reliable when used with this algorithm. King describes an effective chart-based method.
Laplace form of the PID controller
Sometimes it is useful to write the PID regulator in Laplace transform form: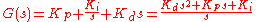
Having the PID controller written in Laplace form and having the transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
of the controlled system makes it easy to determine the closed-loop transfer function of the system.
PID Pole Zero Cancellation
The PID equation can be written in this form: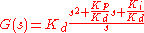
When this form is used it is easy to determine the closed loop transfer function.
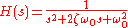
If
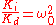
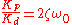
Then
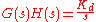
This can be very useful to remove unstable poles
Series/interacting form
Another representation of the PID controller is the series, or interacting form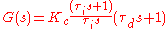
where the parameters are related to the parameters of the standard form through
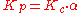 ,
, 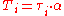 , and
, and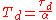
with
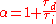 .
.This form essentially consists of a PD and PI controller in series, and it made early (analog) controllers easier to build. When the controllers later became digital, many kept using the interacting form.
Discrete implementation
The analysis for designing a digital implementation of a PID controller in a MicrocontrollerMicrocontroller
A microcontroller is a small computer on a single integrated circuit containing a processor core, memory, and programmable input/output peripherals. Program memory in the form of NOR flash or OTP ROM is also often included on chip, as well as a typically small amount of RAM...
(MCU) or FPGA device requires the standard form of the PID controller to be discretised. Approximations for first-order derivatives are made by backward finite difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
s. The integral term is discretised, with a sampling time
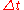 ,as follows,
,as follows,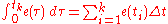
The derivative term is approximated as,
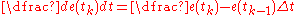
Thus, a velocity algorithm for implementation of the discretised PID controller in a MCU is obtained by differentiating
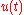 , using the numerical definitions of the first and second derivative and solving for
, using the numerical definitions of the first and second derivative and solving for 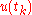 and finally obtaining:
and finally obtaining:
Pseudocode
Here is a simple software loop that implements the PID algorithmin its 'ideal, parallel' form:
previous_error = setpoint - process_feedback
integral = 0
start:
wait(dt)
error = setpoint - process_feedback
integral = integral + (error*dt)
derivative = (error - previous_error)/dt
output = (Kp*error) + (Ki*integral) + (Kd*derivative)
previous_error = error
goto start
PI controller
A PI Controller (proportional-integral controller) is a special case of the PID controller in which the derivative (D) of the error is not used.The controller output is given by
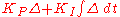
where
 is the error or deviation of actual measured value (PV) from the set-point (SP).
is the error or deviation of actual measured value (PV) from the set-point (SP).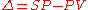 .
.A PI controller can be modelled easily in software such as Simulink
Simulink
Simulink, developed by MathWorks, is a commercial tool for modeling, simulating and analyzing multidomain dynamic systems. Its primary interface is a graphical block diagramming tool and a customizable set of block libraries. It offers tight integration with the rest of the MATLAB environment and...
using a "flow chart" box involving Laplace operators:
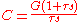
where
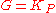 = proportional gain
= proportional gain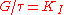 = integral gain
= integral gainSetting a value for
 is often a trade off between decreasing overshoot and increasing settling time.
is often a trade off between decreasing overshoot and increasing settling time.The lack of derivative action may make the system more steady in the steady state in the case of noisy data. This is because derivative action is more sensitive to higher-frequency terms in the inputs.
Without derivative action, a PI-controlled system is less responsive to real (non-noise) and relatively fast alterations in state and so the system will be slower to reach setpoint and slower to respond to perturbations than a well-tuned PID system may be.
PID tutorials
- PID Tutorial
- P.I.D. Without a PhD: a beginner's guide to PID loop theory with sample programming code
- What's All This P-I-D Stuff, Anyhow? Article in Electronic Design
- Shows how to build a PID controller with basic electronic components (pg. 22)
- Virtual PID Controller Laboratory
- Online PID Tuning applet from University of Texas Control Group
- example PID implementation in 16F887 microchip
- PID Control with MATLAB and Simulink
- Improving the Beginner’s PID – Introduction
Special topics and PID control applications
- Proven Methods and Best Practices for PID Control
- PID Control Primer Article in Embedded Systems Programming