
Energy operator
Encyclopedia
In quantum mechanics
, energy
is defined in terms of the energy operator, acting on the wavefunction
of the system.
It is often expressed as:
acting on the wavefunction (the probability amplitude
for different configurations
of the system)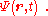
It corresponds to the second term of the left side of the Schrödinger equation
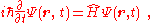
where i is the imaginary unit
, ħ is the reduced Planck constant, and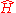 is the Hamiltonian
is the Hamiltonian
operator
.
The energy operator corresponds
to the full energy of a system. The Schrödinger equation describes the space- and time-dependence of slow changing (non-relativistic
) wavefunction of quantum systems. The solution of this equation for bound system is discrete (a set of permitted states, each characterized by an energy level
) which results in the concept of quanta
.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
is defined in terms of the energy operator, acting on the wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
of the system.
It is often expressed as:

acting on the wavefunction (the probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
for different configurations
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
of the system)
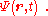
It corresponds to the second term of the left side of the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
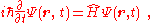
where i is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
, ħ is the reduced Planck constant, and
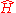 is the Hamiltonian
is the HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
operator
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
.
The energy operator corresponds
Correspondence principle
In physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics reproduces classical physics in the limit of large quantum numbers....
to the full energy of a system. The Schrödinger equation describes the space- and time-dependence of slow changing (non-relativistic
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
) wavefunction of quantum systems. The solution of this equation for bound system is discrete (a set of permitted states, each characterized by an energy level
Energy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
) which results in the concept of quanta
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
.

