
Twelfth root of two
Encyclopedia
The twelfth root of two or 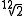 is an algebraic
is an algebraic
irrational number
. It is most important in music theory
, where it represents the frequency
ratio
of a semitone
in equal temperament
.
(which has a ratio of 2:1) into twelve
equal parts.
Applying this value successively to the tones of a chromatic scale, starting from A above middle C
with a frequency of 440 Hz, produces the following sequence of pitch
es:
The final A (880 Hz) is twice the frequency of the lower A (440 Hz), that is, one octave higher.
typically have pitch adjustments of up to ±6%, generally used to match the playback or recording pitch to other music sources having slightly different tunings. Modern recording studios utilize digital pitch shift
ing to achieve the same results, ranging from cents
up to several half-steps.
, historian
, physicist
and mathematician
Zhu Zaiyu, Prince of Zheng of the Ming Dynasty
. In 1584, Zhu published a work 律呂精義 A clear explanation of that which concerns the 律 [equal temperament]. Prince Zhu made note of the difference between his ideal mathematically-tuned 呂 (ancient music instrument), which gave the theoretical music instrument lengths for 12-tone equal temperament correct to 25 places, implemented with an 81-column abacus and calculated the cubic root of the square root of the square root of 2, obtaining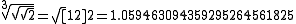 , which coincidentally applied a form of Pythagorean tuning
, which coincidentally applied a form of Pythagorean tuning
.
Calculated again in 1636 by the French mathematician Marin Mersenne
, and as the techniques for calculating logarithm
s develop, the original approach for calculation would eventually become trivial.
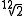 is an algebraic
is an algebraicAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
. It is most important in music theory
Music theory
Music theory is the study of how music works. It examines the language and notation of music. It seeks to identify patterns and structures in composers' techniques across or within genres, styles, or historical periods...
, where it represents the frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
of a semitone
Semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
in equal temperament
Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
.
Numerical value
Its value is 1.05946309435929..., which is slightly more than ≈ 1.0588. Better approximations are ≈ 1.059459 or ≈ 1.0594630948.The equal-tempered chromatic scale
Since a musical interval is a ratio of frequencies, the equal-tempered chromatic scale divides the octaveOctave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
(which has a ratio of 2:1) into twelve
12 (number)
12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten...
equal parts.
Applying this value successively to the tones of a chromatic scale, starting from A above middle C
Middle C
C or Do is the first note of the fixed-Do solfège scale. Its enharmonic is B.-Middle C:Middle C is designated C4 in scientific pitch notation because of the note's position as the fourth C key on a standard 88-key piano keyboard...
with a frequency of 440 Hz, produces the following sequence of pitch
Pitch (music)
Pitch is an auditory perceptual property that allows the ordering of sounds on a frequency-related scale.Pitches are compared as "higher" and "lower" in the sense associated with musical melodies,...
es:
| Note |
Frequency Hz |
Multiplier |
Coefficient (to six places) |
|---|---|---|---|
| A | 440.00 | 2 | 1.000000 |
| A B | 466.16 | 2 | 1.059463 |
| B | 493.88 | 2 | 1.122462 |
| C | 523.25 | 2 | 1.189207 |
| C D | 554.37 | 2 | 1.259921 |
| D | 587.33 | 2 | 1.334839 |
| D E | 622.25 | 2 | 1.414213 |
| E | 659.26 | 2 | 1.498307 |
| F | 698.46 | 2 | 1.587401 |
| F G | 739.99 | 2 | 1.681792 |
| G | 783.99 | 2 | 1.781797 |
| G A | 830.61 | 2 | 1.887748 |
| A | 880.00 | 2 | 2.000000 |
The final A (880 Hz) is twice the frequency of the lower A (440 Hz), that is, one octave higher.
Pitch adjustment
Since the frequency ratio of a semitone is close to 106%, increasing or decreasing the playback speed of a recording by 6% will shift the pitch up or down one semitone, or "half-step". Upscale reel-to-reel magnetic tape recordersReel-to-reel audio tape recording
Reel-to-reel, open reel tape recording is the form of magnetic tape audio recording in which the recording medium is held on a reel, rather than being securely contained within a cassette....
typically have pitch adjustments of up to ±6%, generally used to match the playback or recording pitch to other music sources having slightly different tunings. Modern recording studios utilize digital pitch shift
Pitch shift
Pitch shifting is a sound recording technique in which the original pitch of a sound is raised or lowered. Effects units that raise or lower pitch by a pre-designated musical interval are called "pitch shifters" or "pitch benders".-Pitch/time shifting:...
ing to achieve the same results, ranging from cents
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each...
up to several half-steps.
History
The twelfth root of two was calculated accurately by the Chinese court astronomerAstronomer
An astronomer is a scientist who studies celestial bodies such as planets, stars and galaxies.Historically, astronomy was more concerned with the classification and description of phenomena in the sky, while astrophysics attempted to explain these phenomena and the differences between them using...
, historian
Historian
A historian is a person who studies and writes about the past and is regarded as an authority on it. Historians are concerned with the continuous, methodical narrative and research of past events as relating to the human race; as well as the study of all history in time. If the individual is...
, physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
and mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Zhu Zaiyu, Prince of Zheng of the Ming Dynasty
Ming Dynasty
The Ming Dynasty, also Empire of the Great Ming, was the ruling dynasty of China from 1368 to 1644, following the collapse of the Mongol-led Yuan Dynasty. The Ming, "one of the greatest eras of orderly government and social stability in human history", was the last dynasty in China ruled by ethnic...
. In 1584, Zhu published a work 律呂精義 A clear explanation of that which concerns the 律 [equal temperament]. Prince Zhu made note of the difference between his ideal mathematically-tuned 呂 (ancient music instrument), which gave the theoretical music instrument lengths for 12-tone equal temperament correct to 25 places, implemented with an 81-column abacus and calculated the cubic root of the square root of the square root of 2, obtaining
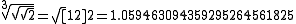 , which coincidentally applied a form of Pythagorean tuning
, which coincidentally applied a form of Pythagorean tuningPythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
.
Calculated again in 1636 by the French mathematician Marin Mersenne
Marin Mersenne
Marin Mersenne, Marin Mersennus or le Père Mersenne was a French theologian, philosopher, mathematician and music theorist, often referred to as the "father of acoustics"...
, and as the techniques for calculating logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s develop, the original approach for calculation would eventually become trivial.
See also
- Just Intonation's history of temperaments.
- Music and mathematicsMusic and mathematicsMusic theorists often use mathematics to understand music. Indeed, mathematics is "the basis of sound" and sound itself "in its musical aspects... exhibits a remarkable array of number properties", simply because nature itself "is amazingly mathematical"...
- Piano key frequenciesPiano key frequenciesThis is a virtual keyboard showing the absolute frequencies in hertz of the notes on a modern piano in twelve-tone equal temperament, with the 49th key, the fifth A , tuned to 440 Hz...
- Scientific pitch notationScientific pitch notationScientific pitch notation is one of several methods that name the notes of the standard Western chromatic scale by combining a letter-name, accidentals, and a number identifying the pitch's octave...
- Well-Tempered Clavier
- Musical tuningMusical tuningIn music, there are two common meanings for tuning:* Tuning practice, the act of tuning an instrument or voice.* Tuning systems, the various systems of pitches used to tune an instrument, and their theoretical bases.-Tuning practice:...
- Nth rootNth rootIn mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...

