Central series
Encyclopedia
In mathematics
, especially in the fields of group theory
and Lie theory
, a central series is a kind of normal series
of subgroup
s or Lie subalgebras, expressing the idea that the commutator is nearly trivial. For groups
, this is an explicit expression that the group is a nilpotent group
, and for matrix ring
s, this is an explicit expression that in some basis the matrix ring consists entirely of upper triangular matrices with constant diagonal.
This article uses the language of group theory; analogous terms are used for Lie algebras.
The lower central series and upper central series (also called the descending central series and ascending central series, respectively), are characteristic series, which, despite the names, are central series if and only if a group is nilpotent
.
such that the successive quotients are central, in the sense that [ G, Ai+1 ] ≤ Ai, where [ G, H ] denotes the commutator subgroup
generated by all g−1h−1gh for g in G and h in H. The subgroups in a central series are always normal subgroup
s of G, so it makes sense to talk about G/Ai. A sequence Ai (as above) of normal subgroups of G is a central series if and only if Ai+1/Ai ≤ Z(G/Ai), where Z(H) = { z in H : zh = hz for all h in H } denotes the center
of a group H.
A central series is analogous in Lie theory
to a flag that is strictly preserved by the adjoint action (more prosaically, a basis in which each element is represented by a strictly upper triangular matrix); compare Engel's theorem.
A group need not have a central series. In fact, a group has a central series if and only if it is a nilpotent group
. If a group has a central series, then there are two central series whose terms are extremal in certain senses. Since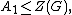
the largest choice for 
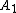is precisely 
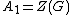. Continuing in this way to choose the largest possible 
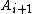given 
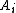produces what is called the upper central series. Dually, one can choose 
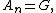and then 
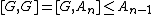. Choosing 
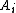minimally given 
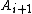such that 
produces what is called the lower central series. These series can be constructed for any group, and if a group has a central series (is a nilpotent group), these procedures will yield central series.
where each Gn+1 = [Gn, G], the subgroup
of G generated
by all commutators [x,y] with x in Gn and y in G. Thus, G2 = [G,G] = G(1), the derived subgroup of G; G3 =[ [ G,G],G], etc. The lower central series is often denoted γn(G) = Gn.
This should not be confused with the derived series, whose terms are G(n) := [G(n−1),G(n−1)], not Gn := [Gn−1,G]. The series are related by G(n) ≤ Gn. In particular, a nilpotent group is a solvable group
, and its derived length is logarithmic in its nilpotency class .
For infinite groups, one can continue the lower central series to infinite ordinal numbers via transfinite recursion: for a limit ordinal λ, define Gλ = ∩ { Gα : α < λ }. If Gλ = 1 for some ordinal λ, then G is said to be a hypocentral group. For every ordinal λ, there is a group G such that Gλ = 1, but Gα ≠ 1 for all α < λ, .
If ω is the first infinite ordinal, then Gω is the smallest normal subgroup of G such that the quotient is residually nilpotent, that is, such that every non-identity element has a non-identity homomorphic image in a nilpotent group . In the field of combinatorial group theory
, it is an important and early result that free group
s are residually nilpotent. In fact the quotients of the lower central series are free abelian groups with a natural basis defined by basic commutators, .
If Gω = Gn for some finite n, then Gω is the smallest normal subgroup of G with nilpotent quotient, and Gω is called the nilpotent residual of G. This is always the case for a finite group, and defines the F1(G) term in the lower Fitting series for G.
If Gω ≠ Gn for all finite n, then G/Gω is not nilpotent, but it is residually nilpotent.
There is no general term for the intersection of all terms of the transfinite lower central series, analogous to the hypercenter (below).
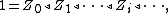
where each successive group is defined by: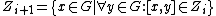
and is called the ith center of G (respectively, second center, third center, etc.). In this case, Z1 is the center
of G, and for each successive group, the factor group Zi+1/Zi is the center of G/Zi, and is called an upper central series quotient.
For infinite groups, one can continue the upper central series to infinite ordinal numbers via transfinite recursion: for a limit ordinal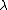
, define 
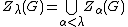. The limit of this process (the union of the higher centers) is called the hypercenter of the group.
If the transfinite upper central series stabilizes at the whole group, then the group is called hypercentral. Hypercentral groups enjoy many properties of nilpotent groups, such as the normalizer condition (the normalizer of a proper subgroup properly contains the subgroup), elements of coprime order commute, and periodic
hypercentral groups are the direct product
of their Sylow p-subgroups . For every ordinal λ there is a group G with Zλ(G) = G, but Zα(G) ≠ G for α < λ, and .
s.
Most simply, a group is abelian if and only if the LCS terminates at the first step (the commutator subgroup is trivial) if and only if the UCS stabilizes at the first step (the center is the entire group). More generally, for a nilpotent group, the length of the LCS and the length of the UCS agree (and is called the nilpotency class of the group).
However, the LCS stabilizes at the zeroth step if and only if it is perfect
, while the UCS stabilizes at the zeroth step if and only if it is centerless, which are distinct concepts, and show that the lengths of the LCS and UCS need not agree in general.
For a perfect group, the UCS always stabilizes by the first step, a fact called Grün's lemma. However, a centerless group may have a very long lower central series: a noncyclic free group
is centerless, but its lower central series does not stabilize until the first infinite ordinal.
s, it is often important to use longer central series. An important class of such central series are the exponent-p central series; that is, a central series whose quotients are elementary abelian group
s, or what is the same, have exponent p. There is a unique most quickly descending such series, the lower exponent-p central series λ defined by:
The second term, λ2(G), is equal to [G, G]Gp = Φ(G), the Frattini subgroup
. The lower exponent-p central series is sometimes simply called the p-central series.
There is a unique most quickly ascending such series, the upper exponent-p central series S defined by:
where Ω(Z(H)) denotes the subgroup generated by (and equal to) the set of central elements of H of order dividing p. The first term, S1(G), is the subgroup generated by the minimal normal subgroups and so is equal to the socle
of G. For this reason the upper exponent-p central series is sometimes known as the socle series or even the Loewy series, though the latter is usually used to indicate a descending series.
Sometimes other refinements of the central series are useful, such as the Jennings series κ defined by:
The Jennings series is named after S. A. Jennings who used the series to describe the Loewy series of the modular group ring
of a p-group.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the fields of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
and Lie theory
Lie theory
Lie theory is an area of mathematics, developed initially by Sophus Lie.Early expressions of Lie theory are found in books composed by Lie with Friedrich Engel and Georg Scheffers from 1888 to 1896....
, a central series is a kind of normal series
Normal series
In mathematics, a subgroup series is a chain of subgroups:1 = A_0 \leq A_1 \leq \cdots \leq A_n = G.Subgroup series can simplify the study of a group to the study of simpler subgroups and their relations, and several subgroup series can be invariantly defined and are important invariants of groups...
of subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s or Lie subalgebras, expressing the idea that the commutator is nearly trivial. For groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, this is an explicit expression that the group is a nilpotent group
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
, and for matrix ring
Matrix ring
In abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
s, this is an explicit expression that in some basis the matrix ring consists entirely of upper triangular matrices with constant diagonal.
This article uses the language of group theory; analogous terms are used for Lie algebras.
The lower central series and upper central series (also called the descending central series and ascending central series, respectively), are characteristic series, which, despite the names, are central series if and only if a group is nilpotent
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
.
Definition
A central series is a sequence of subgroups- {1} = A0 ≤ A1 ≤ … ≤ An = G
such that the successive quotients are central, in the sense that [ G, Ai+1 ] ≤ Ai, where [ G, H ] denotes the commutator subgroup
Commutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
generated by all g−1h−1gh for g in G and h in H. The subgroups in a central series are always normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s of G, so it makes sense to talk about G/Ai. A sequence Ai (as above) of normal subgroups of G is a central series if and only if Ai+1/Ai ≤ Z(G/Ai), where Z(H) = { z in H : zh = hz for all h in H } denotes the center
Center (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of a group H.
A central series is analogous in Lie theory
Lie theory
Lie theory is an area of mathematics, developed initially by Sophus Lie.Early expressions of Lie theory are found in books composed by Lie with Friedrich Engel and Georg Scheffers from 1888 to 1896....
to a flag that is strictly preserved by the adjoint action (more prosaically, a basis in which each element is represented by a strictly upper triangular matrix); compare Engel's theorem.
A group need not have a central series. In fact, a group has a central series if and only if it is a nilpotent group
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
. If a group has a central series, then there are two central series whose terms are extremal in certain senses. Since
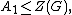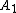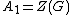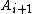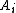the largest choice for is precisely . Continuing in this way to choose the largest possible given produces what is called the upper central series. Dually, one can choose 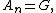and then 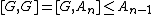. Choosing 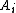minimally given 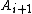such that produces what is called the lower central series. These series can be constructed for any group, and if a group has a central series (is a nilpotent group), these procedures will yield central series.Lower central series
The lower central series (or descending central series) of a group G is the descending series of subgroups- G = G1 ⊵ G2 ⊵ ⋯ ⊵ Gn ⊵ ⋯,
where each Gn+1 = [Gn, G], the subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
by all commutators [x,y] with x in Gn and y in G. Thus, G2 = [G,G] = G(1), the derived subgroup of G; G3 =
This should not be confused with the derived series, whose terms are G(n) := [G(n−1),G(n−1)], not Gn := [Gn−1,G]. The series are related by G(n) ≤ Gn. In particular, a nilpotent group is a solvable group
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
, and its derived length is logarithmic in its nilpotency class .
For infinite groups, one can continue the lower central series to infinite ordinal numbers via transfinite recursion: for a limit ordinal λ, define Gλ = ∩ { Gα : α < λ }. If Gλ = 1 for some ordinal λ, then G is said to be a hypocentral group. For every ordinal λ, there is a group G such that Gλ = 1, but Gα ≠ 1 for all α < λ, .
If ω is the first infinite ordinal, then Gω is the smallest normal subgroup of G such that the quotient is residually nilpotent, that is, such that every non-identity element has a non-identity homomorphic image in a nilpotent group . In the field of combinatorial group theory
Combinatorial group theory
In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations...
, it is an important and early result that free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s are residually nilpotent. In fact the quotients of the lower central series are free abelian groups with a natural basis defined by basic commutators, .
If Gω = Gn for some finite n, then Gω is the smallest normal subgroup of G with nilpotent quotient, and Gω is called the nilpotent residual of G. This is always the case for a finite group, and defines the F1(G) term in the lower Fitting series for G.
If Gω ≠ Gn for all finite n, then G/Gω is not nilpotent, but it is residually nilpotent.
There is no general term for the intersection of all terms of the transfinite lower central series, analogous to the hypercenter (below).
Upper central series
The upper central series (or ascending central series) of a group G is the sequence of subgroups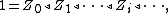where each successive group is defined by:
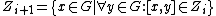
and is called the ith center of G (respectively, second center, third center, etc.). In this case, Z1 is the center
Center (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of G, and for each successive group, the factor group Zi+1/Zi is the center of G/Zi, and is called an upper central series quotient.
For infinite groups, one can continue the upper central series to infinite ordinal numbers via transfinite recursion: for a limit ordinal
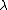, define 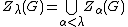. The limit of this process (the union of the higher centers) is called the hypercenter of the group.If the transfinite upper central series stabilizes at the whole group, then the group is called hypercentral. Hypercentral groups enjoy many properties of nilpotent groups, such as the normalizer condition (the normalizer of a proper subgroup properly contains the subgroup), elements of coprime order commute, and periodic
Periodic group
In group theory, a periodic group or a torsion group is a group in which each element has finite order. All finite groups are periodic. The concept of a periodic group should not be confused with that of a cyclic group, although all finite cyclic groups are periodic.The exponent of a periodic group...
hypercentral groups are the direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of their Sylow p-subgroups . For every ordinal λ there is a group G with Zλ(G) = G, but Zα(G) ≠ G for α < λ, and .
Connection between lower and upper central series
There are various connections between the lower central series and upper central series , particularly for nilpotent groupNilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
s.
Most simply, a group is abelian if and only if the LCS terminates at the first step (the commutator subgroup is trivial) if and only if the UCS stabilizes at the first step (the center is the entire group). More generally, for a nilpotent group, the length of the LCS and the length of the UCS agree (and is called the nilpotency class of the group).
However, the LCS stabilizes at the zeroth step if and only if it is perfect
Perfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
, while the UCS stabilizes at the zeroth step if and only if it is centerless, which are distinct concepts, and show that the lengths of the LCS and UCS need not agree in general.
For a perfect group, the UCS always stabilizes by the first step, a fact called Grün's lemma. However, a centerless group may have a very long lower central series: a noncyclic free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
is centerless, but its lower central series does not stabilize until the first infinite ordinal.
Refined central series
In the study of p-groupP-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
s, it is often important to use longer central series. An important class of such central series are the exponent-p central series; that is, a central series whose quotients are elementary abelian group
Elementary Abelian group
In group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; in particular it is a p-group....
s, or what is the same, have exponent p. There is a unique most quickly descending such series, the lower exponent-p central series λ defined by:
- λ1(G) = G, and
- λn+1(G) = [G, λn(G)] (λn(G))p
The second term, λ2(G), is equal to [G, G]Gp = Φ(G), the Frattini subgroup
Frattini subgroup
In mathematics, the Frattini subgroup Φ of a group G is the intersection of all maximal subgroups of G. For the case that G is the trivial group e, which has no maximal subgroups, it is defined by Φ = e...
. The lower exponent-p central series is sometimes simply called the p-central series.
There is a unique most quickly ascending such series, the upper exponent-p central series S defined by:
- S0(G) = 1
- Sn+1(G)/Sn(G) = Ω(Z(G/Sn(G)))
where Ω(Z(H)) denotes the subgroup generated by (and equal to) the set of central elements of H of order dividing p. The first term, S1(G), is the subgroup generated by the minimal normal subgroups and so is equal to the socle
Socle (mathematics)
-Socle of a group:In the context of group theory, the socle of a group G, denoted Soc, is the subgroup generated by the minimal non-trivial normal subgroups of G. The socle is a direct product of minimal normal subgroups...
of G. For this reason the upper exponent-p central series is sometimes known as the socle series or even the Loewy series, though the latter is usually used to indicate a descending series.
Sometimes other refinements of the central series are useful, such as the Jennings series κ defined by:
- κ1(G) = G, and
- κn+1(G) = [G,κn(G)] (κi(G))p, where i is the smallest integer larger than or equal to n/p.
The Jennings series is named after S. A. Jennings who used the series to describe the Loewy series of the modular group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
of a p-group.