
Supersolvable group
Encyclopedia
In mathematics
, a group
is supersolvable (or supersoluble) if it has an invariant normal series
where all the factors are cyclic groups. Supersolvability is stronger than the notion of solvability
.
. G is supersolvable if there exists a normal series

such that each quotient group
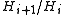 is cyclic and each
is cyclic and each 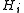 is normal in
is normal in 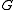 .
.
By contrast, for a solvable group the definition requires each quotient to be abelian. In another direction, a polycyclic group
must have a normal series with each quotient cyclic, but there is no requirement that each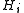 be normal in
be normal in 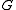 . As every finite soluble group is polycyclic, this can be seen as one of the key differences between the definitions. For a concrete example, the alternating group on four points,
. As every finite soluble group is polycyclic, this can be seen as one of the key differences between the definitions. For a concrete example, the alternating group on four points, 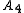 , is solvable but not supersolvable.
, is solvable but not supersolvable.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is supersolvable (or supersoluble) if it has an invariant normal series
Normal series
In mathematics, a subgroup series is a chain of subgroups:1 = A_0 \leq A_1 \leq \cdots \leq A_n = G.Subgroup series can simplify the study of a group to the study of simpler subgroups and their relations, and several subgroup series can be invariantly defined and are important invariants of groups...
where all the factors are cyclic groups. Supersolvability is stronger than the notion of solvability
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
.
Definition
Let G be a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. G is supersolvable if there exists a normal series
Normal series
In mathematics, a subgroup series is a chain of subgroups:1 = A_0 \leq A_1 \leq \cdots \leq A_n = G.Subgroup series can simplify the study of a group to the study of simpler subgroups and their relations, and several subgroup series can be invariantly defined and are important invariants of groups...

such that each quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
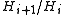 is cyclic and each
is cyclic and each 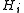 is normal in
is normal in 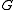 .
.By contrast, for a solvable group the definition requires each quotient to be abelian. In another direction, a polycyclic group
Polycyclic group
In mathematics, a polycyclic group is a solvable group that satisfies the maximal condition on subgroups...
must have a normal series with each quotient cyclic, but there is no requirement that each
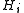 be normal in
be normal in 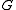 . As every finite soluble group is polycyclic, this can be seen as one of the key differences between the definitions. For a concrete example, the alternating group on four points,
. As every finite soluble group is polycyclic, this can be seen as one of the key differences between the definitions. For a concrete example, the alternating group on four points, 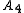 , is solvable but not supersolvable.
, is solvable but not supersolvable.Basic Properties
Some facts about supersolvable groups:- Supersolvable groups are always polycyclicPolycyclic groupIn mathematics, a polycyclic group is a solvable group that satisfies the maximal condition on subgroups...
, and hence solvableSolvable groupIn mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions... - Every finitely generated nilpotent groupNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
is supersolvable. - Every metacyclic groupMetacyclic groupIn group theory, a metacyclic group is an extension of a cyclic group by a cyclic group. That is, it is a group G for which there is a short exact sequence1 \rightarrow K \rightarrow G \rightarrow H \rightarrow 1,\,where H and K are cyclic...
is supersolvable. - The commutator subgroupCommutator subgroupIn mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
of a supersolvable group is nilpotentNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
. - Subgroups and quotient groups of supersolvable groups are supersolvable.
- A finite supersolvable group has an invariant normal series with each factor cyclic of prime order.
- In fact, the primes can be chosen in a nice order: For every prime p, and for π the set of primes greater than p, a finite supersolvable group has a unique Hall π-subgroupHall subgroupIn mathematics, a Hall subgroup of a finite group G is a subgroup whose order is coprime to its index. They are named after the group theorist Philip Hall.- Definitions :A Hall divisor of an integer n is a divisor d of n such that...
. Such groups are sometimes called ordered Sylow tower groups. - Every group of square-free order, and every group with cyclic Sylow subgroups (a Z-group), is supersolvable.
- Every irreducible complex representationRepresentation theory of finite groupsIn mathematics, representation theory is a technique for analyzing abstract groups in terms of groups of linear transformations. See the article on group representations for an introduction...
of a finite supersolvable group is monomial, that is, induced from a linear character of a subgroup. In other words, every supersolvable group is a monomial groupMonomial groupIn mathematics, in the area of algebra studying the character theory of finite groups, an M-group or monomial group is a finite group whose complex irreducible characters are all monomial, that is, induced from characters of degree 1 ....
. - Every maximal subgroupMaximal subgroupIn mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.In group theory, a maximal subgroup H of a group G is a proper subgroup, such that no proper subgroup K contains H strictly. In other words H is a maximal element of the partially...
in a supersolvable group has prime indexIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
. - A finite group is supersolvable if and only if every maximal subgroup has prime index.
- A finite group is supersolvable if and only if every maximal chain of subgroups has the same length. This is important to those interested in the lattice of subgroups of a group, and is sometimes called the Jordan-Dedekind condition.
- By Baum's theorem, every supersolvable finite group has a DFTDiscrete Fourier transformIn mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
algorithm running in time O(n log n).

