
Monad (category theory)
Encyclopedia
In category theory
, a branch of mathematics, a monad, Kleisli
triple, or triple is an (endo-)functor
, together with two natural transformation
s. Monads are used in the theory of pairs of adjoint functors
, and they generalize closure operator
s on partially ordered set
s to arbitrary categories.
The notion of "algebras for a monad" generalizes classical notions from universal algebra
, and in this sense, monads can be thought of as "theories".
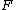 and
and 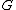 are a pair of adjoint functors
are a pair of adjoint functors
, with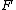 left adjoint to
left adjoint to 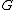 , then the composition
, then the composition 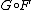 is a monad. Therefore, a monad is an endofunctor. If
is a monad. Therefore, a monad is an endofunctor. If 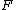 and
and 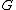 are inverse functors the corresponding monad is the identity functor. In general adjunctions are not equivalences
are inverse functors the corresponding monad is the identity functor. In general adjunctions are not equivalences
— they relate categories of different natures. The monad theory matters as part of the effort to capture what it is that adjunctions 'preserve'. The other half of the theory, of what can be learned likewise from consideration of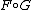 , is discussed under the dual theory of comonads.
, is discussed under the dual theory of comonads.
The monad axioms can be seen at work in a simple example: let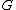 be the forgetful functor
be the forgetful functor
from the category Grp
of groups
to the category Set
of sets. Then as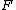 we can take the free group
we can take the free group
functor.
This means that the monad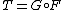
takes a set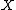 and returns the underlying set of the free group
and returns the underlying set of the free group
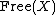 . In this situation, we are given two natural
. In this situation, we are given two natural
morphisms: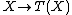
by including any set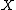 in
in  in the natural way, as strings of length 1. Further,
in the natural way, as strings of length 1. Further,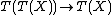
can be made out of a natural concatenation
or 'flattening' of 'strings of strings'. This amounts to two natural transformation
s
and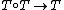
They will satisfy some axioms about identity and associativity
that result from the adjunction properties.
Those axioms are formally similar to the monoid
axioms. They are taken as the definition of a general monad (not assumed a priori to be connected to an adjunction) on a category.
If we specialize to categories arising from partially ordered set
s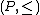 (with a single morphism from
(with a single morphism from  to
to  iff
iff
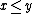 ), then the formalism becomes much simpler: adjoint pairs are Galois connection
), then the formalism becomes much simpler: adjoint pairs are Galois connection
s and monads are closure operators.
Every monad arises from some adjunction, in fact typically from many adjunctions. Two constructions introduced below, the Kleisli category
and the category of Eilenberg-Moore algebras, are extremal solutions of the problem of constructing an adjunction that gives rise to a given monad.
The example about free groups given above can be generalized to any type of algebra in the sense of a variety of algebras in universal algebra
. Thus, every such type of algebra gives rise to a monad on the category of sets. Importantly, the algebra type can be recovered from the monad (as the category of Eilenberg-Moore algebras), so monads can also be seen as generalizing universal algebras. Even more generally, any adjunction is said to be monadic (or tripleable) if it shares this property of being (equivalent to) the Eilenberg-Moore category of its associated monad. Consequently Beck's monadicity theorem
, which gives a criterion for monadicity, can be used to show that an arbitrary adjunction can be treated as a category of algebras in this way.
The notion of monad was invented by Godement in 1958 under the name standard construction. In the 1960s and 1970s, many people used the name triple. The term "monad", which is now standard, is due to Mac Lane.
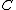 is a category
is a category
, a monad on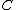 consists of a functor
consists of a functor 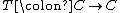 together with two natural transformation
together with two natural transformation
s: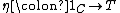 (where
(where 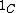 denotes the identity functor on
denotes the identity functor on 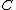 ) and
) and 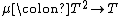 (where
(where 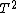 is the functor
is the functor 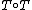 from
from 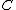 to
to 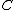 ). These are required to fulfill the following conditions (sometimes called coherence condition
). These are required to fulfill the following conditions (sometimes called coherence condition
s):
We can rewrite these conditions using following commutative diagrams:
See the article on natural transformation
s for the explanation of the notations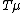 and
and 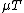 , or see below the commutative diagrams not using these notions:
, or see below the commutative diagrams not using these notions:
The first axiom is akin to the associativity
in monoids
, the second axiom to the existence of an identity element
. Indeed, a monad on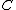 can alternatively be defined as a monoid
can alternatively be defined as a monoid
in the category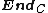 whose objects are the endofunctors of
whose objects are the endofunctors of 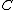 and whose morphisms are the natural transformation
and whose morphisms are the natural transformation
s between them, with the monoidal structure
induced by the composition of endofunctors.
definition is a formal definition of a comonad (or cotriple); this can be said quickly in the terms that a comonad for a category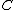 is a monad for the opposite category
is a monad for the opposite category
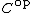 . It is therefore a functor
. It is therefore a functor  from
from 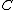 to itself, with a set of axioms for counit and comultiplication that come from reversing the arrows everywhere in the definition just given.
to itself, with a set of axioms for counit and comultiplication that come from reversing the arrows everywhere in the definition just given.
Since a comonoid is not a basic structure in abstract algebra
, this is less familiar at an immediate level.
The importance of the definition comes in a class of theorems from the categorical (and algebraic geometry
) theory of descent
. What was realised in the period 1960 to 1970 is that recognising the categories of coalgebras for a comonad was an important tool of category theory (particularly topos theory). The results involved are based on Beck's theorem. Roughly what goes on is this: while it is simple set theory that a surjective mapping of sets is as good as the imposition of the equivalence relation
'in the same fiber
', for geometric morphisms what you should do is pass to such a coalgebra subcategory.
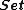 : for a set
: for a set 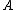 let
let 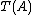 be the power set of
be the power set of 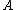 and for a function
and for a function 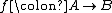 let
let 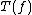 be the function between the power sets induced by taking direct images
be the function between the power sets induced by taking direct images
under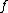 . For every set
. For every set 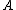 , we have a map
, we have a map 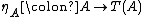 , which assigns to every
, which assigns to every 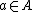 the singleton
the singleton 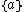 . The function
. The function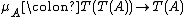
in fact is union
(arbitrary union, not finitary union). These data describe a monad.
Closure operator
s are monads on preorder categories.
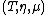 is a given monad on a category
is a given monad on a category 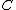 .
.
A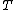 -algebra
-algebra 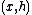 is an object
is an object  of
of 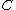 together with an arrow
together with an arrow  of
of 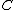 called the structure map of the algebra such that the diagrams
called the structure map of the algebra such that the diagrams
commute.
A morphism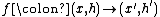 of
of  -algebras is an arrow
-algebras is an arrow 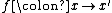 of
of  such that the diagram commutes.
such that the diagram commutes.
The category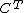 of
of 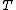 -algebras and their morphisms is called the Eilenberg-Moore category or category of (Eilenberg-Moore) algebras of the monad
-algebras and their morphisms is called the Eilenberg-Moore category or category of (Eilenberg-Moore) algebras of the monad 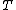 . The forgetful functor
. The forgetful functor 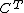 →
→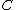 has a left adjoint
has a left adjoint 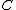 →
→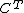 taking
taking  to the free algebra
to the free algebra  .
.
Given the monad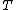 , there exists another "canonical" category
, there exists another "canonical" category 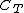 called the Kleisli category
called the Kleisli category
of the monad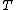 . This category is equivalent to the category of free algebras for the monad
. This category is equivalent to the category of free algebras for the monad 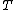 , i. e. the full subcategory of
, i. e. the full subcategory of 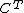 whose objects are of the form
whose objects are of the form 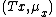 , for
, for  an object of
an object of 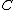 .
.
 between two categories
between two categories 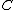 and
and 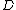 (where
(where 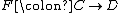 is left adjoint to
is left adjoint to 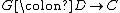 and
and 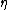 and
and  are respectively the unit and the counit) always defines a monad
are respectively the unit and the counit) always defines a monad 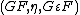 .
.
Conversely, it is interesting to consider the adjunctions which define a given monad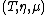 this way. Let
this way. Let 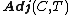 be the category whose objects are the adjunctions
be the category whose objects are the adjunctions 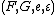 such that
such that 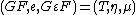 and whose arrows are the morphisms of adjunctions which are the identity on
and whose arrows are the morphisms of adjunctions which are the identity on 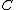 . Then this category has
. Then this category has
An adjunction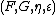 between two categories
between two categories 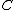 and
and 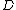 is a monadic adjunction when the category
is a monadic adjunction when the category  is equivalent
is equivalent
to the Eilenberg-Moore category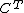 for the monad
for the monad 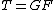 . By extension, a functor
. By extension, a functor 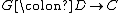 is said to be monadic if it has a left adjoint
is said to be monadic if it has a left adjoint 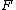 forming a monadic adjunction. Beck's monadicity theorem
forming a monadic adjunction. Beck's monadicity theorem
gives a characterization of monadic functors.
to express types of sequential computation (sometimes with side-effects). See monads in functional programming
, and the more mathematically oriented Wikibook module b:Haskell/Category theory.
In categorical logic, an analogy has been drawn between the monad-comonad theory, and modal logic
via closure operator
s, interior algebra
s, and their relation to models
of S4 and Intuitionistic logics
.
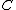 . Monads described above are monads for
. Monads described above are monads for  .
.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a branch of mathematics, a monad, Kleisli
Heinrich Kleisli
Heinrich Kleisli was a mathematician. He is the namesake of several constructions in category theory, including the Kleisli category and Kleisli triples. He is also the namesake of the Kleisli Query System, a tool for integration of heterogeneous databases developed at the University of...
triple, or triple is an (endo-)functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
, together with two natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s. Monads are used in the theory of pairs of adjoint functors
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
, and they generalize closure operator
Closure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
s on partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s to arbitrary categories.
The notion of "algebras for a monad" generalizes classical notions from universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, and in this sense, monads can be thought of as "theories".
Introduction
If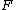 and
and 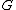 are a pair of adjoint functors
are a pair of adjoint functorsAdjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
, with
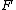 left adjoint to
left adjoint to 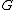 , then the composition
, then the composition 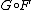 is a monad. Therefore, a monad is an endofunctor. If
is a monad. Therefore, a monad is an endofunctor. If 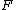 and
and 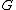 are inverse functors the corresponding monad is the identity functor. In general adjunctions are not equivalences
are inverse functors the corresponding monad is the identity functor. In general adjunctions are not equivalencesEquivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
— they relate categories of different natures. The monad theory matters as part of the effort to capture what it is that adjunctions 'preserve'. The other half of the theory, of what can be learned likewise from consideration of
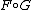 , is discussed under the dual theory of comonads.
, is discussed under the dual theory of comonads.The monad axioms can be seen at work in a simple example: let
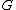 be the forgetful functor
be the forgetful functorForgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
from the category Grp
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
of groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
to the category Set
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
of sets. Then as
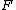 we can take the free group
we can take the free groupFree group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
functor.
This means that the monad
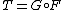
takes a set
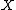 and returns the underlying set of the free group
and returns the underlying set of the free group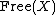 . In this situation, we are given two natural
. In this situation, we are given two naturalmorphisms:
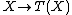
by including any set
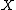 in
in  in the natural way, as strings of length 1. Further,
in the natural way, as strings of length 1. Further,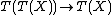
can be made out of a natural concatenation
Concatenation
In computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
or 'flattening' of 'strings of strings'. This amounts to two natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s

and
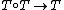
They will satisfy some axioms about identity and associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
that result from the adjunction properties.
Those axioms are formally similar to the monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
axioms. They are taken as the definition of a general monad (not assumed a priori to be connected to an adjunction) on a category.
If we specialize to categories arising from partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s
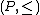 (with a single morphism from
(with a single morphism from  to
to  iff
iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
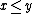 ), then the formalism becomes much simpler: adjoint pairs are Galois connection
), then the formalism becomes much simpler: adjoint pairs are Galois connectionGalois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
s and monads are closure operators.
Every monad arises from some adjunction, in fact typically from many adjunctions. Two constructions introduced below, the Kleisli category
Kleisli category
In category theory, a Kleisli category is a category naturally associated to any monad T. It is equivalent to the category of free T-algebras. The Kleisli category is one of two extremal solutions to the question Does every monad arise from an adjunction? The other extremal solution is the...
and the category of Eilenberg-Moore algebras, are extremal solutions of the problem of constructing an adjunction that gives rise to a given monad.
The example about free groups given above can be generalized to any type of algebra in the sense of a variety of algebras in universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
. Thus, every such type of algebra gives rise to a monad on the category of sets. Importantly, the algebra type can be recovered from the monad (as the category of Eilenberg-Moore algebras), so monads can also be seen as generalizing universal algebras. Even more generally, any adjunction is said to be monadic (or tripleable) if it shares this property of being (equivalent to) the Eilenberg-Moore category of its associated monad. Consequently Beck's monadicity theorem
Beck's monadicity theorem
In category theory, a branch of mathematics, Beck's monadicity theorem asserts that a functorU: C \to Dis monadic if and only if# U has a left adjoint;# U reflects isomorphisms; and...
, which gives a criterion for monadicity, can be used to show that an arbitrary adjunction can be treated as a category of algebras in this way.
The notion of monad was invented by Godement in 1958 under the name standard construction. In the 1960s and 1970s, many people used the name triple. The term "monad", which is now standard, is due to Mac Lane.
Formal definition
If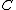 is a category
is a categoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a monad on
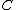 consists of a functor
consists of a functor 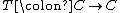 together with two natural transformation
together with two natural transformationNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s:
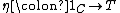 (where
(where 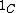 denotes the identity functor on
denotes the identity functor on 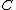 ) and
) and 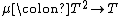 (where
(where 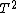 is the functor
is the functor 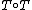 from
from 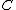 to
to 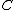 ). These are required to fulfill the following conditions (sometimes called coherence condition
). These are required to fulfill the following conditions (sometimes called coherence conditionCoherence condition
In mathematics, and particularly category theory a coherence condition is a collection of conditions requiring that various compositions of elementary morphisms are equal...
s):
-
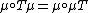 (as natural transformations
(as natural transformations 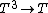 );
); -
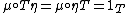 (as natural transformations
(as natural transformations 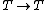 ; here
; here 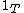 denotes the identity transformation from
denotes the identity transformation from 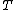 to
to 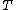 ).
).
We can rewrite these conditions using following commutative diagrams:
See the article on natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s for the explanation of the notations
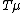 and
and 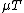 , or see below the commutative diagrams not using these notions:
, or see below the commutative diagrams not using these notions:The first axiom is akin to the associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
in monoids
Monoid (category theory)
In category theory, a monoid in a monoidal category is an object M together with two morphisms* \mu : M\otimes M\to M called multiplication,* and \eta : I\to M called unit,...
, the second axiom to the existence of an identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. Indeed, a monad on
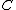 can alternatively be defined as a monoid
can alternatively be defined as a monoidMonoid (category theory)
In category theory, a monoid in a monoidal category is an object M together with two morphisms* \mu : M\otimes M\to M called multiplication,* and \eta : I\to M called unit,...
in the category
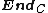 whose objects are the endofunctors of
whose objects are the endofunctors of 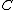 and whose morphisms are the natural transformation
and whose morphisms are the natural transformationNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s between them, with the monoidal structure
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
induced by the composition of endofunctors.
Comonads and their importance
The categorical dualDual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
definition is a formal definition of a comonad (or cotriple); this can be said quickly in the terms that a comonad for a category
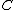 is a monad for the opposite category
is a monad for the opposite categoryOpposite category
In category theory, a branch of mathematics, the opposite category or dual category Cop of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite...
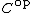 . It is therefore a functor
. It is therefore a functor  from
from 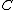 to itself, with a set of axioms for counit and comultiplication that come from reversing the arrows everywhere in the definition just given.
to itself, with a set of axioms for counit and comultiplication that come from reversing the arrows everywhere in the definition just given.Since a comonoid is not a basic structure in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, this is less familiar at an immediate level.
The importance of the definition comes in a class of theorems from the categorical (and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
) theory of descent
Descent (category theory)
In mathematics, the idea of descent has come to stand for a very general idea, extending the intuitive idea of 'gluing' in topology. Since the topologists' glue is actually the use of equivalence relations on topological spaces, the theory starts with some ideas on identification.A sophisticated...
. What was realised in the period 1960 to 1970 is that recognising the categories of coalgebras for a comonad was an important tool of category theory (particularly topos theory). The results involved are based on Beck's theorem. Roughly what goes on is this: while it is simple set theory that a surjective mapping of sets is as good as the imposition of the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
'in the same fiber
Fiber
Fiber is a class of materials that are continuous filaments or are in discrete elongated pieces, similar to lengths of thread.They are very important in the biology of both plants and animals, for holding tissues together....
', for geometric morphisms what you should do is pass to such a coalgebra subcategory.
Examples
The rich set of examples is given by adjunctions (see "Monads and adjunctions"), and the free group example mentioned above belongs to that set. Another example, on the category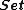 : for a set
: for a set 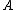 let
let 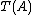 be the power set of
be the power set of 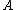 and for a function
and for a function 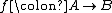 let
let 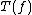 be the function between the power sets induced by taking direct images
be the function between the power sets induced by taking direct imagesImage (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
under
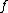 . For every set
. For every set 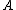 , we have a map
, we have a map 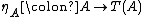 , which assigns to every
, which assigns to every 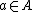 the singleton
the singleton 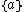 . The function
. The function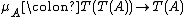
in fact is union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
(arbitrary union, not finitary union). These data describe a monad.
Closure operator
Closure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
s are monads on preorder categories.
Algebras for a monad
Suppose that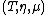 is a given monad on a category
is a given monad on a category 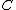 .
.A
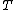 -algebra
-algebra 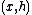 is an object
is an object  of
of 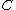 together with an arrow
together with an arrow  of
of 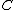 called the structure map of the algebra such that the diagrams
called the structure map of the algebra such that the diagrams
| and |
commute.
A morphism
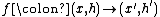 of
of 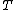 -algebras is an arrow
-algebras is an arrow  of
of 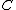 such that the diagram commutes.
such that the diagram commutes.The category
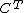 of
of 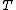 -algebras and their morphisms is called the Eilenberg-Moore category or category of (Eilenberg-Moore) algebras of the monad
-algebras and their morphisms is called the Eilenberg-Moore category or category of (Eilenberg-Moore) algebras of the monad 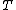 . The forgetful functor
. The forgetful functor 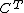 →
→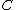 has a left adjoint
has a left adjoint 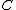 →
→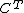 taking
taking  to the free algebra
to the free algebra  .
.Given the monad
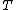 , there exists another "canonical" category
, there exists another "canonical" category 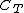 called the Kleisli category
called the Kleisli categoryKleisli category
In category theory, a Kleisli category is a category naturally associated to any monad T. It is equivalent to the category of free T-algebras. The Kleisli category is one of two extremal solutions to the question Does every monad arise from an adjunction? The other extremal solution is the...
of the monad
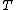 . This category is equivalent to the category of free algebras for the monad
. This category is equivalent to the category of free algebras for the monad 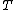 , i. e. the full subcategory of
, i. e. the full subcategory of 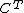 whose objects are of the form
whose objects are of the form 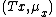 , for
, for  an object of
an object of 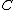 .
.Monads and adjunctions
An adjunction between two categories
between two categories 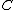 and
and 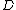 (where
(where 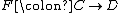 is left adjoint to
is left adjoint to 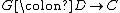 and
and 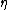 and
and  are respectively the unit and the counit) always defines a monad
are respectively the unit and the counit) always defines a monad 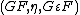 .
.Conversely, it is interesting to consider the adjunctions which define a given monad
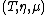 this way. Let
this way. Let 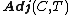 be the category whose objects are the adjunctions
be the category whose objects are the adjunctions 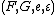 such that
such that 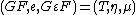 and whose arrows are the morphisms of adjunctions which are the identity on
and whose arrows are the morphisms of adjunctions which are the identity on 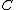 . Then this category has
. Then this category has
- an initial object
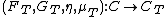 , where
, where 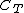 is the Kleisli category,
is the Kleisli category, - a terminal object
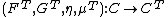 , where
, where 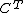 is the Eilenberg-Moore category.
is the Eilenberg-Moore category.
An adjunction
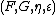 between two categories
between two categories 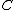 and
and 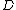 is a monadic adjunction when the category
is a monadic adjunction when the category  is equivalent
is equivalentEquivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
to the Eilenberg-Moore category
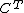 for the monad
for the monad 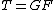 . By extension, a functor
. By extension, a functor 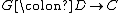 is said to be monadic if it has a left adjoint
is said to be monadic if it has a left adjoint 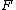 forming a monadic adjunction. Beck's monadicity theorem
forming a monadic adjunction. Beck's monadicity theoremBeck's monadicity theorem
In category theory, a branch of mathematics, Beck's monadicity theorem asserts that a functorU: C \to Dis monadic if and only if# U has a left adjoint;# U reflects isomorphisms; and...
gives a characterization of monadic functors.
Uses
Monads are used in functional programmingFunctional programming
In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
to express types of sequential computation (sometimes with side-effects). See monads in functional programming
Monads in functional programming
In functional programming, a monad is a programming structure that represents computations. Monads are a kind of abstract data type constructor that encapsulate program logic instead of data in the domain model...
, and the more mathematically oriented Wikibook module b:Haskell/Category theory.
In categorical logic, an analogy has been drawn between the monad-comonad theory, and modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
via closure operator
Closure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
s, interior algebra
Interior algebra
In abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic...
s, and their relation to models
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
of S4 and Intuitionistic logics
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
.
Generalization
It is possible to define monads in a 2-category2-category
In category theory, a 2-category is a category with "morphisms between morphisms"; that is, where each hom set itself carries the structure of a category...
 . Monads described above are monads for
. Monads described above are monads for  .
.See also
- Distributive law between monadsDistributive law between monadsIn category theory, an abstract branch of mathematics, distributive laws between monads are a way to express abstractly that two algebraic structures distribute one over the other one....
- Strong monad
- Monad (disambiguation) for other meanings of the term.
- PolyadPolyadIn mathematics, polyad is a concept of category theory introduced by Jean Bénabou in generalising monads. A polyad in a bicategory D is a bicategory morphism Φ from a locally punctual bicategory C to D,...
External links
- Monads Five short lectures (with one appendix).
- John Baez's This Week's Finds in Mathematical Physics (Week 89) covers monads in 2-categories.

