Strong monad
Encyclopedia
In category theory
, a strong monad over a monoidal category
 is a monad
is a monad
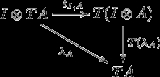
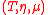 together with a natural transformation
together with a natural transformation
 , called (tensorial) strength, such that the diagrams
, called (tensorial) strength, such that the diagrams
and
commute for every object ,
,  and
and  .
.
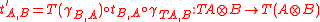 .
.
A strong monad T is said to be commutative when the diagram
commutes for all objects and
and  .
.
One interesting fact about commutative strong monads is that they are "the same as" symmetric monoidal monads. More explicitly,
and the conversion between one and the other presentation is bijective.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a strong monad over a monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
 is a monad
is a monadMonad (category theory)
In category theory, a branch of mathematics, a monad, Kleisli triple, or triple is an functor, together with two natural transformations...
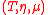 together with a natural transformation
together with a natural transformationNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
 , called (tensorial) strength, such that the diagrams
, called (tensorial) strength, such that the diagrams
 ,
,  ,
,
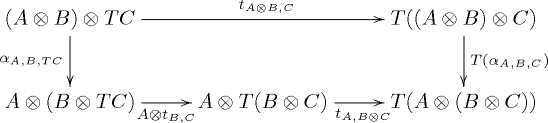 ,
,
and
commute for every object
 ,
,  and
and  .
.Commutative strong monads
For every strong monad T on a symmetric monoidal category, a costrength natural transformation can be defined by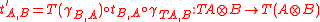 .
.A strong monad T is said to be commutative when the diagram
commutes for all objects
 and
and  .
.One interesting fact about commutative strong monads is that they are "the same as" symmetric monoidal monads. More explicitly,
- a commutative strong monad
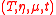 defines a symmetric monoidal monad
defines a symmetric monoidal monad  by
by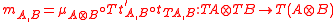
- and conversely a symmetric monoidal monad
 defines a commutative strong monad
defines a commutative strong monad 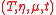 by
by
and the conversion between one and the other presentation is bijective.



