
Molecular mechanics
Encyclopedia
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
to model molecular systems. The potential energy of all systems in molecular mechanics is calculated using force field
Force field (chemistry)
In the context of molecular modeling, a force field refers to the form and parameters of mathematical functions used to describe the potential energy of a system of particles . Force field functions and parameter sets are derived from both experimental work and high-level quantum mechanical...
s. Molecular mechanics can be used to study small molecules as well as large biological systems or material assemblies with many thousands to millions of atoms.
All-atomistic molecular mechanics methods have the following properties:
- Each atom is simulated as a single particle
- Each particle is assigned a radius (typically the van der Waals radiusVan der Waals radiusThe van der Waals radius, r, of an atom is the radius of an imaginary hard sphere which can be used to model the atom for many purposes. It is named after Johannes Diderik van der Waals, winner of the 1910 Nobel Prize in Physics, as he was the first to recognise that atoms had a finite size and to...
), polarizability, and a constant net charge (generally derived from quantum calculations and/or experiment) - Bonded interactions are treated as "springs" with an equilibrium distance equal to the experimental or calculated bond length
Variations on this theme are possible; for example, many simulations have historically used a "united-atom" representation in which methyl and methylene groups were represented as a single particle, and large protein systems are commonly simulated using a "bead" model that assigns two to four particles per amino acid
Amino acid
Amino acids are molecules containing an amine group, a carboxylic acid group and a side-chain that varies between different amino acids. The key elements of an amino acid are carbon, hydrogen, oxygen, and nitrogen...
.
Functional form
Force field (chemistry)
In the context of molecular modeling, a force field refers to the form and parameters of mathematical functions used to describe the potential energy of a system of particles . Force field functions and parameter sets are derived from both experimental work and high-level quantum mechanical...
in Chemistry, calculates the molecular system's potential energy (E) in a given conformation as a sum of individual energy terms.

where the components of the covalent and noncolvalent contributions are given by the following summations:


The exact functional form of the potential function
Potential energy of protein
Potential Energy of Protein =A protein folds into the state of lowest potential energy. Potential energy of a protein can be evaluated with quantum chemistry. However required computation is too much...
, or force field, depends on the particular simulation program being used. Generally the bond and angle terms are modeled as harmonic potentials
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
centered around equilibrium bond-length values derived from experiment or theoretical calculations of electronic structure performed with software which does ab-initio type calculations such as Gaussian
GAUSSIAN
Gaussian is a computational chemistry software program initially released in 1970 by John Pople and his research group at Carnegie-Mellon University as Gaussian 70. It has been continuously updated since then...
. For accurate reproduction of vibrational spectra, the Morse potential
Morse potential
The Morse potential, named after physicist Philip M. Morse, is a convenient model for the potential energy of a diatomic molecule. It is a better approximation for the vibrational structure of the molecule than the quantum harmonic oscillator because it explicitly includes the effects of bond...
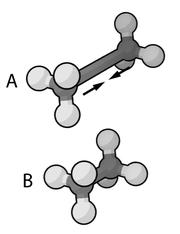
can be used instead, at computational cost. The dihedral or torsional terms typically have multiple minima and thus cannot be modeled as harmonic oscillators, though their specific functional form varies with the implementation. This class of terms may include "improper" dihedral terms, which function as correction factors for out-of-plane deviations (for example, they can be used to keep benzene
Benzene
Benzene is an organic chemical compound. It is composed of 6 carbon atoms in a ring, with 1 hydrogen atom attached to each carbon atom, with the molecular formula C6H6....
rings planar).
The non-bonded terms are much more computationally costly to calculate in full, since a typical atom is bonded to only a few of its neighbors, but interacts with every other atom in the molecule. Fortunately the van der Waals
Van der Waals force
In physical chemistry, the van der Waals force , named after Dutch scientist Johannes Diderik van der Waals, is the sum of the attractive or repulsive forces between molecules other than those due to covalent bonds or to the electrostatic interaction of ions with one another or with neutral...
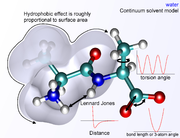
term falls off rapidly – it is typically modeled using a "6–12 Lennard-Jones potential
Lennard-Jones potential
The Lennard-Jones potential is a mathematically simple model that approximates the interaction between a pair of neutral atoms or molecules. A form of the potential was first proposed in 1924 by John Lennard-Jones...
", which means that attractive forces fall off with distance as r−6 and repulsive forces as r−12, where r represents the distance between two atoms. The repulsive part r−12 is however unphysical, because repulsion increases exponentially. Description of van der Waals forces by the Lennard-Jones 6–12 potential introduces inaccuracies, which become significant at short distances. Generally a cutoff radius is used to speed up the calculation so that atom pairs whose distances are greater than the cutoff have a van der Waals interaction energy of zero.
The electrostatic terms are notoriously difficult to calculate well because they do not fall off rapidly with distance, and long-range electrostatic interactions are often important features of the system under study (especially for proteins). The Quantized Valence Bonds' Molecular Mechanics (QVBMM) force field (implemented in Exorga, Incorporated's StruMM3D product, once named STR3DI32) is unique in molecular mechanics as the only one to directly use all lone pair interactions in all of its energy calculations. The basic functional form is the Coulomb potential
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
, which only falls off as r−1. A variety of methods are used to address this problem, the simplest being a cutoff radius similar to that used for the van der Waals terms. However, this introduces a sharp discontinuity between atoms inside and atoms outside the radius. Switching or scaling functions that modulate the apparent electrostatic energy are somewhat more accurate methods that multiply the calculated energy by a smoothly varying scaling factor from 0 to 1 at the outer and inner cutoff radii. Other more sophisticated but computationally intensive methods are known as particle mesh Ewald (PME) and the multipole algorithm
Fast Multipole Method
The fast multipole method is a mathematical technique that was developed to speed up the calculation of long-ranged forces in the n-body problem...
.
In addition to the functional form of each energy term, a useful energy function must be assigned parameters for force constants, van der Waals multipliers, and other constant terms. These terms, together with the equilibrium bond, angle, and dihedral values, partial charge values, atomic masses and radii, and energy function definitions, are collectively known as a force field
Force field (chemistry)
In the context of molecular modeling, a force field refers to the form and parameters of mathematical functions used to describe the potential energy of a system of particles . Force field functions and parameter sets are derived from both experimental work and high-level quantum mechanical...
. Parameterization is typically done through agreement with experimental values and theoretical calculations results.
Each force field is parameterized to be internally consistent, but the parameters are generally not transferable from one force field to another. For example, the MM3 force field has 46 sets of parameters for oxygen and 18 sets for carbon (in different functional groups). MM3 has no parameters for lone pairs of electrons. On the other hand, the molecular recognition features of StruMM3D (which inputs only molecule's atom types and their coordinates) enables it to use only two parameters for each hybridization type of each atom (covalent radius and electronegativity), and it is parameterized for actively using lone pairs of electrons in its calculations. These molecular recognition features of StruMM3D allow for an easy usage of data from MM3 files. However, starting with the simple Cartesian coordinate data, as for example from a diffraction study, one would require considerable effort to produce a MM3 file. Most molecular modelers, and StruMM3D, can generate MM2, XYZ, and other files which can be read by MM3.
Areas of application
The prototypical molecular mechanics application is energy minimization. That is, the force fieldForce field (chemistry)
In the context of molecular modeling, a force field refers to the form and parameters of mathematical functions used to describe the potential energy of a system of particles . Force field functions and parameter sets are derived from both experimental work and high-level quantum mechanical...
is used as an optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
criterion and the (local) minimum searched by an appropriate algorithm (e.g. steepest descent
Gradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
). Global energy optimization can be accomplished using simulated annealing
Simulated annealing
Simulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
, the Metropolis algorithm and other Monte Carlo
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
methods, or using different deterministic methods of discrete or continuous optimization. The main aim of optimization methods is finding the lowest energy conformation of a molecule or identifying a set of low-energy conformers that are in equilibrium with each other. The force field represents only the enthalpic
Enthalpy
Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
component of free energy
Gibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
, and only this component is included during energy minimization. However, the analysis of equilibrium between different states requires also conformational entropy
Conformational entropy
Conformational entropy is the entropy associated with the physical arrangement of a polymer chain that assumes a compact or globular state in solution. The concept is most commonly applied to biological macromolecules such as proteins and RNA, but can also be used for polysaccharides and other...
be included, which is possible but rarely done.
Molecular mechanics potential energy functions have been used to calculate binding constants, protein folding kinetics, protonation equilibria, active site coordinates, and to design binding sites
Protein design
Protein design is the design of new protein molecules, either from scratch or by making calculated variations on a known structure. The use of rational design techniques for proteins is a major aspect of protein engineering....
.
Environment and solvation
There are several ways of defining the environment surrounding the molecule or molecules of interest in molecular mechanics. A system can be simulated in vacuum (known as a gas-phase simulation) with no surrounding environment at all, but this is usually not desirable because it introduces artifacts in the molecular geometry, especially in charged molecules. Surface charges that would ordinarily interact with solvent molecules instead interact with each other, producing molecular conformations that are unlikely to be present in any other environment. The "best" way to solvate a system is to place explicit water molecules in the simulation box with the molecules of interest and treat the water molecules as interacting particles like those in the molecule. A variety of water modelWater model
In computational chemistry, classical water models are used for the simulation of water clusters, liquid water, and aqueous solutions with explicit solvent. These models use the approximations of molecular mechanics...
s exist with increasing levels of complexity, representing water as a simple hard sphere (a united-atom approach), as three separate particles with fixed bond angles, or even as four or five separate interaction centers to account for unpaired electrons on the oxygen atom. Unsurprisingly, the more complex the water model, the more computationally intensive the simulation. A compromise approach has been found in implicit solvation
Implicit solvation
Implicit solvation is a method of representing solvent as a continuous medium instead of individual “explicit” solvent molecules most often used in molecular dynamics simulations and in other applications of molecular mechanics...
, which replaces the explicitly represented water molecules with a mathematical expression that reproduces the average behavior of water molecules (or other solvents such as lipids). This method is useful for preventing artifacts that arise from vacuum simulations and reproduces bulk solvent properties well, but cannot reproduce situations in which individual water molecules have interesting interactions with the molecules under study.

