
Logarithmic differentiation
Encyclopedia
In calculus
, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate
function
s by employing the logarithmic derivative
of a function ƒ,
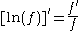
The technique is often performed in cases where it is easier to differentiate the logarithm of a function rather than the function itself. Logarithmic differentiation relies on the chain rule
as well as properties of logarithms (in particular, the natural logarithm
, or logarithmic to the base e) to transform products into sums and divisions into subtractions, and can also applied to functions raised to the power of variables or functions.
However, the principle can be implemented, at least in part, in the differentiation of almost all differentiable function
s, providing that these functions are non-zero.
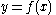
logarithmic differentiation typically begins by taking the natural logarithm, or the logarithm to the base e, on both sides, remembering to take absolute values
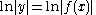
After implicit differentiation
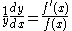
Multiplication by y is then done to eliminate 1/y and leave only dy/dx on the left:
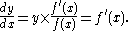
The method is used because the properties of logarithms provide avenues to quickly simplify complicated functions to be differentiated. These properties can be manipulated after the taking of natural logarithms on both sides and before the preliminary differentiation. The most commonly used logarithm laws:
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s by employing the logarithmic derivative
Logarithmic derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formulawhere f ′ is the derivative of f....
of a function ƒ,
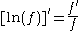
The technique is often performed in cases where it is easier to differentiate the logarithm of a function rather than the function itself. Logarithmic differentiation relies on the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
as well as properties of logarithms (in particular, the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
, or logarithmic to the base e) to transform products into sums and divisions into subtractions, and can also applied to functions raised to the power of variables or functions.
However, the principle can be implemented, at least in part, in the differentiation of almost all differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
s, providing that these functions are non-zero.
Overview
For a function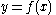
logarithmic differentiation typically begins by taking the natural logarithm, or the logarithm to the base e, on both sides, remembering to take absolute values
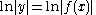
After implicit differentiation
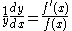
Multiplication by y is then done to eliminate 1/y and leave only dy/dx on the left:
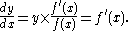
The method is used because the properties of logarithms provide avenues to quickly simplify complicated functions to be differentiated. These properties can be manipulated after the taking of natural logarithms on both sides and before the preliminary differentiation. The most commonly used logarithm laws:
-
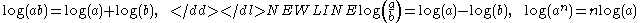
General case
Using capital pi notation,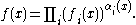
Application of natural logarithms results in (with capital sigma notation)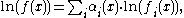
and after differentiation,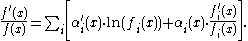
Rearrange to get the derivative of the original function,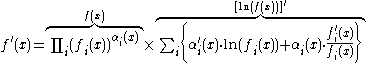
Products
A natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
is applied to a product of two functions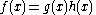
to transform the product into a sum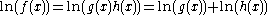
Differentiate by applying the chainChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
and the sumSum rule in differentiationIn calculus, the sum rule in differentiation is a method of finding the derivative of a function that is the sum of two other functions for which derivatives exist. This is a part of the linearity of differentiation. The sum rule in integration follows from it...
rules
and, after rearranging, get
Quotients
A natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
is applied to a quotient of two functions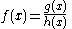
to transform the division into a subtraction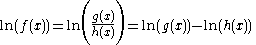
Differentiate by applying the chainChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
and the sumSum rule in differentiationIn calculus, the sum rule in differentiation is a method of finding the derivative of a function that is the sum of two other functions for which derivatives exist. This is a part of the linearity of differentiation. The sum rule in integration follows from it...
rules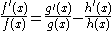
and, after rearranging, get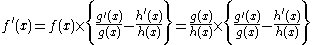
After multiplying out and using the common denominator formula the result is the same as if after applying the quotient rule directly to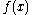 .
.
Composite exponent
For a function of the form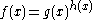
The natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
transforms the exponentiation into a product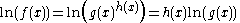
Differentiate by applying the chainChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
and the productSum rule in differentiationIn calculus, the sum rule in differentiation is a method of finding the derivative of a function that is the sum of two other functions for which derivatives exist. This is a part of the linearity of differentiation. The sum rule in integration follows from it...
rules
and, after rearranging, get
See also
- Darboux derivativeDarboux derivativeThe Darboux derivative of a map between a manifold and a Lie group is a variant of the standard derivative. In a certain sense, it is arguably a more natural generalization of the single-variable derivative...
, Maurer–Cartan form for generalizations to arbitrary Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s - List of logarithm topics
- List of logarithmic identities
- Darboux derivative

