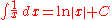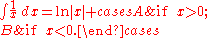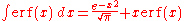Lists of integrals
Encyclopedia
Integration
is the basic operation in integral calculus. While differentiation
has easy rules by which the derivative of a complicated function
can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. This page lists some of the most common antiderivatives.
Not all closed-form expression
s have closed-form antiderivatives; this study forms the subject of differential Galois theory
, which was initially developed by Joseph Liouville
in the 1830s and 1840s, leading to Liouville's theorem
which classifies which expressions have closed form antiderivatives. A simple example of a function without a closed form antiderivative is e−x2, whose antiderivative is (up to constants) the error function
.
Since 1968 there is the Risch algorithm
for determining indefinite integrals that can be expressed in term of elementary functions, typically using a computer algebra system
. Integrals that cannot be expressed using elementary functions can be manipulated symbolically using general functions such as the Meijer G-function
.
s:
Gradshteyn, Ryzhik, Jeffrey, Zwillinger's Table of Integrals, Series, and Products contains a large collection of results. An even larger, multivolume table is the Integrals and Series by Prudnikov, Brychkov, and Marichev
(with volumes 1–3 listing integrals and series of elementary and special functions
, volume 4–5 are tables of Laplace transforms). More compact collections can be found in e.g. Brychkov, Marichev, Prudnikov's Tables of Indefinite Integrals, or as chapters in Zwillinger's CRC Standard Mathematical Tables and Formulae, Bronstein and Semendyayev's Handbook of Mathematics (Springer) and Oxford Users' Guide to Mathematics (Oxford Univ. Press), and other mathematical handbooks.
Other useful resources include Abramowitz and Stegun
and the Bateman Manuscript Project
. Both works contain many identities concerning specific integrals, which are organized with the most relevant topic instead of being collected into a separate table. Two volumes of the Bateman Manuscript are specific to integral transforms.
There are several web sites which have tables of integrals and integrals on demand. Wolfram Alpha
can show results, and for some simpler expressions, also the intermediate steps of the integration. Wolfram Research also operates another online service, the Wolfram Mathematica Online Integrator.
that can only be determined if something about the value of the integral at some point is known. Thus each function has an infinite number of antiderivatives.
These formulas only state in another form the assertions in the table of derivatives.
, then C does not need to be the same on both sides of the singularity. The forms below normally assume the Cauchy principal value
around a singularity in the value of C but this is not in general necessary. For instance in
there is a singularity at 0 and the integral becomes infinite there. If the integral above was used to give a definite integral between -1 and 1 the answer would be 0. This however is only the value assuming the Cauchy principal value for the integral around the singularity. If the integration was done in the complex plane the result would depend on the path around the origin, in this case the singularity contributes −iπ when using a path above the origin and iπ for a path below the origin. A function on the real line could use a completely different value of C on either side of the origin as in:
These rational functions have a non-integrable singularity at 0 for a ≤ −1.
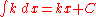
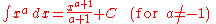 (Cavalieri's quadrature formula)
(Cavalieri's quadrature formula)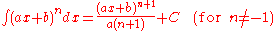
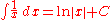
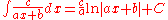
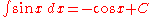
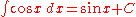
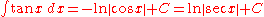
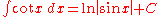
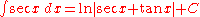






Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
is the basic operation in integral calculus. While differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
has easy rules by which the derivative of a complicated function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. This page lists some of the most common antiderivatives.
Historical development of integrals
A compilation of a list of integrals (Integraltafeln) and techniques of integral calculus was published by the German mathematician Meyer Hirsch in 1810. These tables were republished in the United Kingdom in 1823. More extensive tables were compiled in 1858 by the Dutch mathematician David de Bierens de Haan. A new edition was published in 1862. These tables, which contain mainly integrals of elementary functions, remained in use until the middle of the 20th century. They were then replaced by the much more extensive tables of Gradshteyn and Ryzhik. In Gradshteyn and Ryzhik, integrals originating from the book by de Bierens are denoted by BI.Not all closed-form expression
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
s have closed-form antiderivatives; this study forms the subject of differential Galois theory
Differential Galois theory
In mathematics, differential Galois theory studies the Galois groups of differential equations.Whereas algebraic Galois theory studies extensions of algebraic fields, differential Galois theory studies extensions of differential fields, i.e. fields that are equipped with a derivation, D. Much of...
, which was initially developed by Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
in the 1830s and 1840s, leading to Liouville's theorem
Liouville's theorem (differential algebra)
In mathematics, Liouville's theorem, originally formulated by Joseph Liouville in the 1830s and 1840s, places an important restriction on antiderivatives that can be expressed as elementary functions....
which classifies which expressions have closed form antiderivatives. A simple example of a function without a closed form antiderivative is e−x2, whose antiderivative is (up to constants) the error function
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
.
Since 1968 there is the Risch algorithm
Risch algorithm
The Risch algorithm, named after Robert Henry Risch, is an algorithm for the calculus operation of indefinite integration . The algorithm transforms the problem of integration into a problem in algebra. It is based on the form of the function being integrated and on methods for integrating rational...
for determining indefinite integrals that can be expressed in term of elementary functions, typically using a computer algebra system
Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
. Integrals that cannot be expressed using elementary functions can be manipulated symbolically using general functions such as the Meijer G-function
Meijer G-Function
In mathematics, the G-function was introduced by as a very general function intended to include most of the known special functions as particular cases. This was not the only attempt of its kind: the generalized hypergeometric function and the MacRobert E-function had the same aim, but Meijer's...
.
Lists of integrals
More detail may be found on the following pages for the lists of integralIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s:
- List of integrals of rational functions
- List of integrals of irrational functions
- List of integrals of trigonometric functions
- List of integrals of inverse trigonometric functions
- List of integrals of hyperbolic functions
- List of integrals of inverse hyperbolic functions
- List of integrals of exponential functions
- List of integrals of logarithmic functions
- List of integrals of Gaussian functions
Gradshteyn, Ryzhik, Jeffrey, Zwillinger's Table of Integrals, Series, and Products contains a large collection of results. An even larger, multivolume table is the Integrals and Series by Prudnikov, Brychkov, and Marichev
Oleg Igorevich Marichev
Oleg Igorewitsch Marichev is a Russian mathematician. In 1949 he moved to Minsk with his parents. Graduated from the University of Belarus, where he continued to study for Ph.D. dergee. His scientific supervisor was Fedor Gakhov. He is the co-author of a comprehensive table of intergals. Around...
(with volumes 1–3 listing integrals and series of elementary and special functions
Special functions
Special functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
, volume 4–5 are tables of Laplace transforms). More compact collections can be found in e.g. Brychkov, Marichev, Prudnikov's Tables of Indefinite Integrals, or as chapters in Zwillinger's CRC Standard Mathematical Tables and Formulae, Bronstein and Semendyayev's Handbook of Mathematics (Springer) and Oxford Users' Guide to Mathematics (Oxford Univ. Press), and other mathematical handbooks.
Other useful resources include Abramowitz and Stegun
Abramowitz and Stegun
Abramowitz and Stegun is the informal name of a mathematical reference work edited by Milton Abramowitz and Irene Stegun of the U.S. National Bureau of Standards...
and the Bateman Manuscript Project
Bateman Manuscript Project
The Bateman Manuscript Project was a major effort at collation and encyclopedic compilation of the mathematical theory of special functions. It resulted in the eventual publication of five important reference volumes, under the editorship of Arthur Erdélyi....
. Both works contain many identities concerning specific integrals, which are organized with the most relevant topic instead of being collected into a separate table. Two volumes of the Bateman Manuscript are specific to integral transforms.
There are several web sites which have tables of integrals and integrals on demand. Wolfram Alpha
Wolfram Alpha
Wolfram Alpha is an answer-engine developed by Wolfram Research. It is an online service that answers factual queries directly by computing the answer from structured data, rather than providing a list of documents or web pages that might contain the answer as a search engine might...
can show results, and for some simpler expressions, also the intermediate steps of the integration. Wolfram Research also operates another online service, the Wolfram Mathematica Online Integrator.
Integrals of simple functions
C is used for an arbitrary constant of integrationArbitrary constant of integration
In calculus, the indefinite integral of a given function is only defined up to an additive constant, the constant of integration. This constant expresses an ambiguity inherent in the construction of antiderivatives...
that can only be determined if something about the value of the integral at some point is known. Thus each function has an infinite number of antiderivatives.
These formulas only state in another form the assertions in the table of derivatives.
Integrals with a singularity
When there is a singularity in the function being integrated such that the integral becomes undefined, i.e., it is not Lebesgue integrableLebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
, then C does not need to be the same on both sides of the singularity. The forms below normally assume the Cauchy principal value
Cauchy principal value
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
around a singularity in the value of C but this is not in general necessary. For instance in
there is a singularity at 0 and the integral becomes infinite there. If the integral above was used to give a definite integral between -1 and 1 the answer would be 0. This however is only the value assuming the Cauchy principal value for the integral around the singularity. If the integration was done in the complex plane the result would depend on the path around the origin, in this case the singularity contributes −iπ when using a path above the origin and iπ for a path below the origin. A function on the real line could use a completely different value of C on either side of the origin as in:
Rational functions
- more integrals: List of integrals of rational functions
These rational functions have a non-integrable singularity at 0 for a ≤ −1.
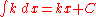
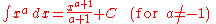 (Cavalieri's quadrature formula)
(Cavalieri's quadrature formula)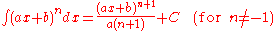
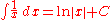
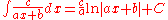
Exponential functions
- more integrals: List of integrals of exponential functions
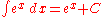
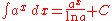
Logarithms
- more integrals: List of integrals of logarithmic functions


Trigonometric functions
- more integrals: List of integrals of trigonometric functions
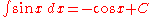
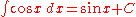
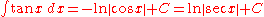
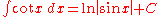
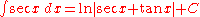
-
- (See Integral of the secant functionIntegral of the secant functionThe integral of the secant function of trigonometry was the subject of one of the "outstanding open problems of the mid-seventeenth century", solved in 1668 by James Gregory. In 1599, Edward Wright evaluated the integral by numerical methods – what today we would call Riemann sums...
. This result was a well-known conjecture in the 17th century.)
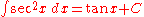

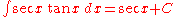
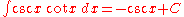
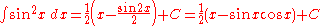
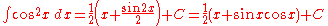
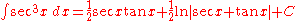
- (see integral of secant cubed)
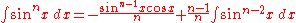

- (See Integral of the secant function
Inverse trigonometric functions
- more integrals: List of integrals of inverse trigonometric functions






Hyperbolic functions
- more integrals: List of integrals of hyperbolic functions
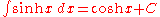
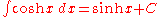
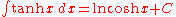
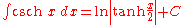
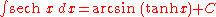
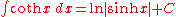
Inverse hyperbolic functions
- more integrals: List of integrals of inverse hyperbolic functions
-

-

-
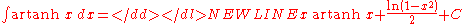
-
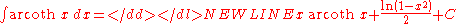
-
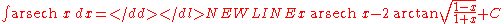
-

Products of functions proportional to their second derivatives
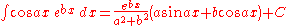



Absolute value functions



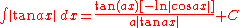

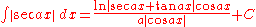

Special functions
Ci, Si: Trigonometric integralTrigonometric integralIn mathematics, the trigonometric integrals are a family of integrals which involve trigonometric functions. A number of the basic trigonometric integrals are discussed at the list of integrals of trigonometric functions.-Sine integral:...
s, Ei: Exponential integralExponential integralIn mathematics, the exponential integral is a special function defined on the complex plane given the symbol Ei.-Definitions:For real, nonzero values of x, the exponential integral Ei can be defined as...
, li: Logarithmic integral functionLogarithmic integral functionIn mathematics, the logarithmic integral function or integral logarithm li is a special function. It occurs in problems of physics and has number theoretic significance, occurring in the prime number theorem as an estimate of the number of prime numbers less than a given value.-Integral...
, erf: Error functionError functionIn mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
Definite integrals lacking closed-form antiderivatives
There are some functions whose antiderivatives cannot be expressed in closed formClosed-form expressionIn mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
. However, the values of the definite integrals of some of these functions over some common intervals can be calculated. A few useful integrals are given below.
 (see also Gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
(see also Gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
)
 (the Gaussian integralGaussian integralThe Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
(the Gaussian integralGaussian integralThe Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
)
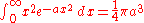 for a > 0
for a > 0
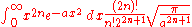 for a > 0, n is 1, 2, 3, ... and !! is the double factorial.
for a > 0, n is 1, 2, 3, ... and !! is the double factorial.
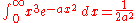 when a > 0
when a > 0
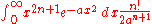 for a > 0, n = 0, 1, 2, ....
for a > 0, n = 0, 1, 2, ....
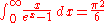 (see also Bernoulli numberBernoulli numberIn mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
(see also Bernoulli numberBernoulli numberIn mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
)
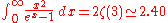
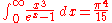
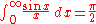 (see sinc function and Sine integral)
(see sinc function and Sine integral)
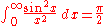
 (if n is an even integer and
(if n is an even integer and  )
)
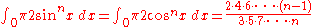 (if
(if  is an odd integer and
is an odd integer and  )
)
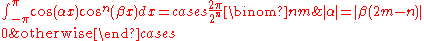 (for
(for  integers with
integers with  and
and  , see also Binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
, see also Binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
)
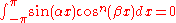 (for
(for  real and
real and  non-negative integer, see also SymmetrySymmetrySymmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
non-negative integer, see also SymmetrySymmetrySymmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
)
 (for
(for  integers with
integers with  and
and  , see also Binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
, see also Binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
)
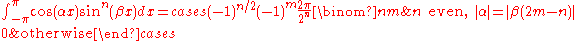 (for
(for  integers with
integers with  and
and  , see also Binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
, see also Binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
)
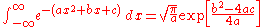 (where
(where  is the exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
is the exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
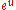 , and
, and  )
)
 (where
(where 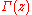 is the Gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
is the Gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
)
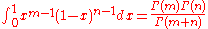 (the Beta function)
(the Beta function)
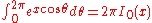 (where
(where 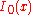 is the modified Bessel functionBessel functionIn mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
is the modified Bessel functionBessel functionIn mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind)
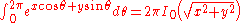
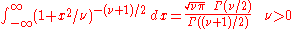 , this is related to the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
, this is related to the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the Student's t-distribution)
The method of exhaustionMethod of exhaustionThe method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
provides a formula for the general case when no antiderivative exists:
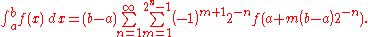
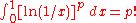
The "sophomore's dream"
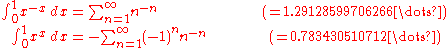
attributed to Johann BernoulliJohann BernoulliJohann Bernoulli was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family...
.
See also
- Indefinite sum
- Incomplete Gamma functionIncomplete gamma functionIn mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
- List of mathematical series
- List of limits
- Symbolic integrationSymbolic integrationIn calculus symbolic integration is the problem of finding a formula for the antiderivative, or indefinite integral, of a given function f, i.e...
Historical
- Meyer Hirsch, Integraltafeln, oder, Sammlung von Integralformeln (Duncker und Humblot, Berlin, 1810)
- Meyer Hirsch, Integral Tables, Or, A Collection of Integral Formulae (Baynes and son, London, 1823) [English translation of Integraltafeln]
- David Bierens de Haan, Nouvelles Tables d'Intégrales définies (Engels, Leiden, 1862)
- Benjamin O. Pierce A short table of integrals - revised edition (Ginn & co., Boston, 1899)
Tables of integrals
- S.O.S. Mathematics: Tables and Formulas (warning: may serve popunders)
- Paul's Online Math Notes
- A. Dieckmann, Table of Integrals (Elliptic Functions, Square Roots, Inverse Tangents and More Exotic Functions): Indefinite Integrals Definite Integrals
- Math Major: A Table of Integrals
- O'Brien, Francis J. Jr. Integrals Derived integrals of exponential and logarithmic functions
- Rule-based Mathematics Precisely defined indefinite integration rules covering a wide class of integrands
Derivations
Online service
Open source programs
-
-
-
-
-
-