There are many relations among the uniform polyhedron

Uniform polyhedron

A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...

.
Some are obtained by truncating the vertices of the regular or quasi-regular polyhedron.
Others share the same vertices and edges as other polyhedron.
The grouping below exhibit some of these relations.

The vertex figure of a polyhedron

The relations can be made apparent by examining the vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

s.
obtained by listing the faces adjacent to each vertex (remember that for uniform polyhedra all vertices are the same, that is vertex-transitive

Vertex-transitive

In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...

). For example the cube has
vertex figure 4.4.4 that is three adjacent square faces.
The possible faces are

• 3 - equilateral triangle
• 4 - square
• 5 - regular pentagon
• 6 - regular hexagon
• 8 - regular octagon
• 10 - regular decagon
• 5/2 - pentagram
• 8/3 - octagram
• 10/3 - decagram

Some faces will appear with reverse orientation which is written here as

• -3 - a triangle with reverse orientation (often written as 3/2)

Others pass through the origin which we write as

• 6* - hexagon passing through the origin

The Wythoff symbol

Wythoff symbol

In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....

 relates the polyhedron to spherical triangles

Spherical trigonometry

Spherical trigonometry is a branch of spherical geometry which deals with polygons on the sphere and the relationships between the sides and the angles...

. Wythoff symbols are written
p|q r, p q|r, p q r| where the spherical triangle has angles π/p,π/q,π/r, the bar indicates the position of the vertices in relation to the triangle.
Johnson (2000) classified uniform polyhedra according to the following:

1. Regular (regular polygonal vertex figures): p^q, Wythoff symbol q|p 2
2. Quasi-regular (rectangular or ditrigonal vertex figures): p.q.p.q 2|p q, or p.q.p.q.p.q, Wythoff symbol 3|p q
3. Versi-regular (orthodiagonal vertex figures), p.q*.-p.q*, Wythoff symbol q q|p
4. Truncated regular (isosceles triangular vertex figures): p.p.q, Wythoff symbol q 2|p
5. Versi-quasi-regular (dipteroidal vertex figures), p.q.p.r Wythoff symbol q r|p
6. Quasi-quasi-regular (trapezoidal vertex figures): p*.q.p*.-r q.r|p or p.q*.-p.q* p q r|
7. Truncated quasi-regular (scalene triangular vertex figures), p.q.r Wythoff symbol p q r|
8. Snub quasi-regular (pentagonal, hexagonal, or octagonal vertex figures), Wythoff symbol p q r|
9. Prisms (truncated hosohedra),
10. Antiprisms and crossed antiprisms (snub dihedra)

The format of each figure follows the same basic pattern

1. image of polyhedron
2. name of polyhedron
3. alternate names (in brackets)
4. Wythoff symbol
5. Numbering systems: W - number used by Wenninger in polyhedra models, U - uniform indexing, K - Kaleido indexing, C - numbering used in Coxeter et al. 'Uniform Polyhedra'.
6. Number of vertices V, edges E, Faces F and number of faces by type.
7. Euler characteristic χ = V - E + F

The vertex figures are on the left, followed by the Point groups in three dimensions#The seven remaining point groups, either tetrahedral T_d, octahedral O_h or icosahedral I_h.

Regular polyhedra and their truncated forms

Column A lists all the regular polyhedra,
column B list their truncated forms.
Regular polyhedra all have vertex figures p^r: p.p.p etc. and Whycroft symbol
p|q r. The truncated forms have vertex figure q.q.r (where q=2p and r) and Whycroft p q|r.

vertex figure	group	A: regular: p.p.p	B: truncated regular: p.p.r
3.3.3 3.6.6	Td	Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... 3|2 3 W1, U01, K06, C15 V 4,E 6,F 4=4{3} χ=2	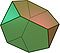Truncated tetrahedron Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... 2 3|3 W6, U02, K07, C16 V 12,E 18,F 8=4{3}+4{6} χ=2
3.3.3.3 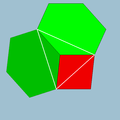4.6.6	Oh	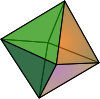Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... 4|2 3, 34 W2, U05, K10, C17 V 6,E 12,F 8=8{3} χ=2	Truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... 2 4|3 W7, U08, K13, C20 V 24,E 36,F 14=6{4}+8{6} χ=2
4.4.4 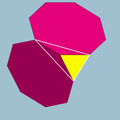3.8.8	Oh	Hexahedron Hexahedron A hexahedron is any polyhedron with six faces, although usually implies the cube as a regular hexahedron with all its faces square, and three squares around each vertex....   (Cube) 3|2 4 W3, U06, K11, C18 V 8,E 12,F 6=6{4} χ=2	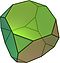Truncated hexahedron Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... 2 3|4 W8, U09, K14, C21 V 24,E 36,F 14=8{3}+6{8} χ=2
3.3.3.3.3 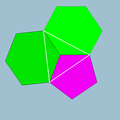5.6.6	Ih	Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... 5|2 3 W4, U22, K27, C25 V 12,E 30,F 20=20{3} χ=2	Truncated icosahedron Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... 2 5|3 W9, U25, K30, C27 E 60,V 90,F 32=12{5}+20{6} χ=2
5.5.5 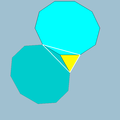4.10.10	Ih	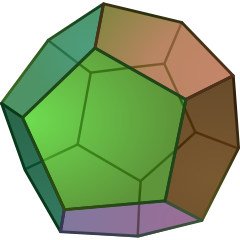Dodecahedron 3|2 5 W5, U23, K28, C26 V 20,E 30,F 12=12{5} χ=2	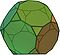Truncated dodecahedron Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :... 2 3|5 W10, U26, K31, C29 V 60,E 90,F 32=20{3}+12{10} χ=2
5.5.5.5.5 5/2.10.10	Ih	Great dodecahedron 5/2|2 5 W21, U35, K40, C44 V 12,E 30,F 12=12{5} χ=-6	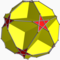Truncated great dodecahedron 25/2|5 W75, U37, K42, C47 V 60,E 90,F 24=12{5/2}+12{10} χ=-6
3.3.3.3.3 5/2.6.6.	Ih	Great icosahedron (16th stellation of icosahedron) 5/2|2 3 W41, U53, K58, C69 V 12,E 30,F 20=20{3} χ=2	Great truncated icosahedron 25/2|3 W95, U55, K60, C71 V 60,E 90,F 32=12{5/2}+20{6} χ=2
5/2.5/2.5/2.5/2.5/2	Ih	Small stellated dodecahedron 5|25/2 W20, U34, K39, C43 V 12,E 30,F 12=12{5/2} χ=-6
5/2.5/2.5/2	Ih	Great stellated dodecahedron 3|25/2 W22, U52, K57, C68 V 20,E 30,F 12=12{5/2} χ=2

In addition there are three quasi-truncated forms. These also class as truncated-regular polyhedra.

vertex figures	Group Oh	Group Ih	Group Ih
3.8/3.8/3 5.10/3.10/3 3.10/3.10/3	Stellated truncated hexahedron (Quasitruncated hexahedron) (stellatruncated cube) 2 3|4/3 W92, U19, K24, C66 V 24,E 36,F 14=8{3}+6{8/3} χ=2	Small stellated truncated dodecahedron (Quasitruncated small stellated dodecahedron) (Small stellatruncated dodecahedron) 2 5|5/3 W97, U58, K63 V 60,E 90,F 24=12{5}+12{10/3} χ=-6	Great stellated truncated dodecahedron (Quasitruncated great stellated dodecahedron) (Great stellatruncated dodecahedron) 2 3|5/3 W104, U66, K71, C83 V 60,E 90,F 32=20{3}+12{10/3} χ=2

Truncated forms of quasi-regular polyhedra

Column A lists some quasi-regular polyhedra,
column B lists normal truncated forms,
column C shows quasi-truncated forms,
column D shows a different method of truncation.
These truncated forms all have a vertex figure p.q.r and a
Wythoff
symbol p q r|.

vertex figure	group	A: quasi-regular: p.q.p.q	B: truncated quasi-regular: p.q.r	C: truncated quasi-regular: p.q.r	D: truncated quasi-regular: p.q.r
3.4.3.4 4.6.8 4.6.8/3 8.6.8/3	Oh	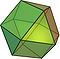Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... 2|3 4 W11, U07, K12, C19 V 12,E 24,F 14=8{3}+6{4} χ=2	Great rhombicuboctahedron (Rhombitruncated cuboctahedron) (Truncated cuboctahedron) 2 3 4| W15, U11, K16, C23 V 48,E 72,F 26=12{4}+8{6}+6{8} χ=2	Great truncated cuboctahedron (Quasitruncated cuboctahedron) 2 34/3| W93, U20, K25, C67 V 48,E 72,F 26=12{4}+8{6}+6{8/3} χ=2	Cubitruncated cuboctahedron Cubitruncated cuboctahedron In geometry, the cubitruncated cuboctahedron is a nonconvex uniform polyhedron, indexed as U16.- Convex hull :Its convex hull is a nonuniform truncated cuboctahedron.- Cartesian coordinates :... (Cuboctatruncated cuboctahedron) 3 44/3| W79, U16, K21, C52 V 48,E 72,F 20=8{6}+6{8}+6{8/3} χ=-4
3.5.3.5 4.6.10 4.6.10/3 10.6.10/3	Ih	Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... 2|3 5 W12, U24, K29, C28 V 30,E 60,F 32=20{3}+12{5} χ=2	Great rhombicosidodecahedron (Rhombitruncated icosidodecahedron) (Truncated icosidodecahedron) 2 3 5| W16, U28, K33, C31 V 120,E 180,F 62=30{4}+20{6}+12{10} χ=2	Great truncated icosidodecahedron (Great quasitruncated icosidodecahedron) 2 35/3| W108, U68, K73, C87 V 120,E 180,F 62=30{4}+20{6}+12{10/3} χ=2	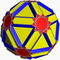Icositruncated dodecadodecahedron Icositruncated dodecadodecahedron In geometry, the icositruncated dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U45.- Convex hull :Its convex hull is a nonuniform great rhombicosidodecahedron.- Cartesian coordinates :... (Icosidodecatruncated icosidodecahedron) 3 55/3| W84, U45, K50, C57 V 120,E 180,F 44=20{6}+12{10}+12{10/3} χ=-16
5/2.5.5/2.5 4.10.10/3	Ih	Dodecadodecahedron 2 5|5/2 W73, U36, K41, C45 V 30,E 60, F 24=12{5}+12{5/2} χ=-6		Truncated dodecadodecahedron (Quasitruncated dodecahedron) 2 55/3| W98, U59, K64, C75 V 120,E 180,F 54=30{4}+12{10}+12{10/3} χ=-6
3.5/2.3.5/2	Ih	Great icosidodecahedron 2 3|5/2 W94, U54, K59, C70 V 30,E 60, F 32=20{3}+12{5/2} χ=2

Regular

These are all mentioned elsewhere, but this table shows some relations.
They are all regular apart from the tetrahemihexahedron which is versi-regular.

vertex figure	V	E	group	regular	regular/versi-regular
3.3.3.3 3.4*.-3.4*	6	12	Oh	Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... 4|2 3 W2, U05, K10, C17 F 8=8{3} χ=2	Tetrahemihexahedron Tetrahemihexahedron In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 6 vertices and 12 edges, and 7 faces: 4 triangular and 3 square. Its vertex figure is a crossed quadrilateral. It has Coxeter-Dynkin diagram of .... 3/23|2 W67, U04, K09, C36 F 7=4{3}+3{4} χ=1
3.3.3.3.3 5.5.5.5.5	12	30	Ih	Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... 5|2 3 W4, U22, K27 F 20=20{3} χ=2	Great dodecahedron 5/2|2 5 W21, U35, K40, C44 F 12=12{5} χ=-6
5/2.5/2.5/2.5/2.5/2 3.3.3.3.3	12	30	Ih	Small stellated dodecahedron 5|25/2 W20, U34, K39, C43 F 12=12{5/2} χ=-6	Great icosahedron (16th stellation of icosahedron) 5/2|2 3 W41, U53, K58, C69 F 20=20{3} χ=2

Quasi-regular and versi-regular

Rectangular vertex figures, or crossed rectangles
first column are quasi-regular second and third columns are hemihedra with
faces passing through the origin, called versi-regular by some authors.

vertex figure	V	E	group	quasi-regular: p.q.p.q	versi-regular: p.s*.-p.s*	versi-regular: q.s*.-q.s*
3.4.3.4 3.6*.-3.6* 4.6*.-4.6*	12	24	Oh	Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... 2|3 4 W11, U07, K12, C19 F 14=8{3}+6{4} χ=2	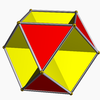Octahemioctahedron Octahemioctahedron In geometry, the octahemioctahedron is a nonconvex uniform polyhedron, indexed as U3. Its vertex figure is a crossed quadrilateral.It is one of nine hemipolyhedra with 4 hexagonal faces passing through the model center.- Related polyhedra :... 3/23|3 W68, U03, K08, C37 F 12=8{3}+4{6} χ=0	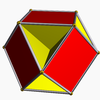Cubohemioctahedron Cubohemioctahedron In geometry, the cubohemioctahedron is a nonconvex uniform polyhedron, indexed as U15. Its vertex figure is a crossed quadrilateral.A nonconvex polyhedron has intersecting faces which do not represent new edges or faces... 4/34|3 W78, U15, K20, C51 F 10=6{4}+4{6} χ=-2
3.5.3.5 3.10*.-3.10* 5.10*.-5.10*	30	60	Ih	Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... 2|3 5 W12, U24, K29, C28 F 32=20{3}+12{5} χ=2	Small icosihemidodecahedron Small icosihemidodecahedron In geometry, the small icosihemidodecahedron is a uniform star polyhedron, indexed as U49. Its vertex figure alternates two regular triangles and decagons as a crossed quadrilateral.... 3/23|5 W89, U49, K54, C63 F 26=20{3}+6{10} χ=-4	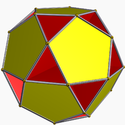Small dodecahemidodecahedron Small dodecahemidodecahedron In geometry, the small dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U51. Its vertex figure alternates two regular pentagons and decagons as a crossed quadrilateral.... 5/45|5 W91, U51, K56, 65 F 18=12{5}+6{10} χ=-12
3.5/2.3.5/2 3.10*.-3.10* 5/2.10*.-5/2.10*	30	60	Ih	Great icosidodecahedron 2|5/23 W94, U54, K59, C70 F 32=20{3}+12{5/2} χ=2	Great icosihemidodecahedron Great icosihemidodecahedron In geometry, the great icosihemidodecahedron is a nonconvex uniform polyhedron, indexed as U71. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with 6 decagrammic faces passing through the model center.- Related polyhedra :... 3 3|5/3 W106, U71, K76, C85 F 26=20{3}+6{10/3} χ=-4	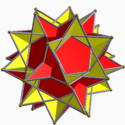Great dodecahemidodecahedron Great dodecahemidodecahedron In geometry, the great dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U70. Its vertex figure is a crossed quadrilateral.... 5/35/2|5/3 W107, U70, K75, C86 F 18=12{5/2}+6{10/3} χ=-12
5.5/2.5.5/2 5.6*.-5.6* 5/2.6*.-5/2.6*	30	60	Ih	Dodecadodecahedron 2|5/25 W73, U36, K41, C45 F 24=12{5}+12{5/2} χ=-6	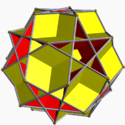Great dodecahemicosahedron Great dodecahemicosahedron In geometry, the great dodecahemicosahedron is a nonconvex uniform polyhedron, indexed as U65. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with ten hexagonal faces passing through the model center.- Related polyhedra :... 5/45|3 W102, U65, K70, C81 F 22=12{5}+10{6} χ=-8	Small dodecahemicosahedron Small dodecahemicosahedron In geometry, the small dodecahemicosahedron is a nonconvex uniform polyhedron, indexed as U62. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with ten hexagonal faces passing through the model center.- Related polyhedra :... 5/35/2|3 W100, U62, K67, C78 F 22=12{5/2}+10{6} χ=-8

Ditrigonal regular and versi-regular

Ditrigonal (that is di(2) -tri(3)-ogonal) vertex figures are the 3-fold analog of a rectangle. These are all quasi-regular as all edges are isomorphic.
The compound of 5-cubes shares the same set of edges and vertices.
The cross forms have a non-orientable vertex figure so the "-" notation has not been used and the "*" faces pass near rather than through the origin.

vertex figure	V	E	group	ditrogonal	crossed-ditrogonal	crossed-ditrogonal
5/2.3.5/2.3.5/2.3 5/2.5*.5/2.5*.5/2.5* 3.5*.3.5*.3.5*	20	60	Ih	Small ditrigonal icosidodecahedron Small ditrigonal icosidodecahedron In geometry, the small ditrigonal icosidodecahedron is a nonconvex uniform polyhedron, indexed as U30.-Related polyhedra:Its convex hull is a regular dodecahedron... 3|5/23 W70, U30, K35, C39 F 32=20{3}+12{5/2} χ=-8	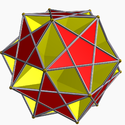Ditrigonal dodecadodecahedron Ditrigonal dodecadodecahedron In geometry, the Ditrigonal dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U41.- Related polyhedra :Its convex hull is a regular dodecahedron... 3|5/35 W80, U41, K46, C53 F 24=12{5}+12{5/2} χ=-16	Great ditrigonal icosidodecahedron 3/2|3 5 W87, U47, K52, C61 F 32=20{3}+12{5} χ=-8

versi-quasi-regular and quasi-quasi-regular

Group III: trapezoid or crossed trapezoid vertex figures.
The first column include the convex rhombic polyhedra, created by inserting two squares
into the vertex figures of the Cuboctahedron and Icosidodecahedron.

vertex figure	V	E	group	trapezoid: p.q.r.q	crossed-trapezoid: p.s*.-r.s*	crossed-trapezoid: q.s*.-q.s*
3.4.4.4 3.8*.-4.8* 4.8*.-4.8*	24	48	Oh	Small rhombicuboctahedron (rhombicuboctahedron) 3 4|2 W13, U10, K15, C22 F 26=8{3}+(6+12){4} χ=2	Small cubicuboctahedron Small cubicuboctahedron In geometry, the small cubicuboctahedron is a uniform star polyhedron, indexed as U13. It has 20 faces , 48 edges, and 24 vertices. Its vertex figure is a crossed quadrilateral.- Related polyhedra :... 3/24|4 W69, U13, K18, C38 F 20=8{3}+6{4}+6{8} χ=-4	Small rhombihexahedron Small rhombihexahedron In geometry, the small rhombihexahedron is a nonconvex uniform polyhedron, indexed as U18. It has 18 faces , 48 edges, and 24 vertices. Its vertex figure is an antiparallelogram.-Related polyhedra:... 2 3/2 4| W86, U18, K23, C60 F 18=12{4}+6{8} χ=-6
3.8/3.4.8/3 3.4*.-4.4* 8/3.4*.-8/3.4*	24	48	Oh	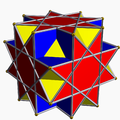Great cubicuboctahedron Great cubicuboctahedron In geometry, the great cubicuboctahedron is a nonconvex uniform polyhedron, indexed as U14.- Related polyhedra :It shares the vertex arrangement with the convex truncated cube and two other nonconvex uniform polyhedra... 3 4|4/3 W77, U14, K19, C50 F 20=8{3}+6{4}+6{8/3} χ=-4	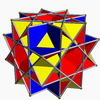Nonconvex great rhombicuboctahedron (Quasirhombicuboctahedron) 3/24|2 W85, U17, K22, C59 F 26=8{3}+(6+12){4} χ=2	Great rhombihexahedron Great rhombihexahedron In geometry, the great rhombihexahedron is a nonconvex uniform polyhedron, indexed as U21. Its dual is the great rhombihexacron. Its vertex figure is a crossed quadrilateral.- Related polyhedra :... 2 4/33/2| W103, U21, K26, C82 F 18=12{4}+6{8/3} χ=-6
3.4.5.4 3.10*.-5.10* 4.10*.-4.10*	60	120	Ih	Small rhombicosidodecahedron (rhombicosidodecahedron) 3 5|2 W14, U27, K32, C30 F 62=20{3}+30{4}+12{5} χ=2	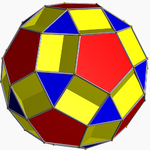Small dodecicosidodecahedron Small dodecicosidodecahedron In geometry, the small dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U33. Its vertex figure is a crossed quadrilateral.-Related polyhedra:... 3/25|5 W72, U33, K38, C42 F 44=20{3}+12{5}+12{10} χ=-16	Small rhombidodecahedron Small rhombidodecahedron In geometry, the small rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U39. Its vertex figure is a crossed quadrilateral.- Related polyhedra :... 25/25| W74, U39, K44, C46 F 42=30{4}+12{10} χ=-18
5/2.4.5.4 5/2.6*.-5.6* 4.6*.-4.6*	60	120	Ih	Rhombidodecadodecahedron 5/25|2 W76, U38, K43, C48 F 54=30{4}+12{5}+12{5/2} χ=-6	Icosidodecadodecahedron Icosidodecadodecahedron In geometry, the icosidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U44. Its vertex figure is a crossed quadrilateral.- Related polyhedra :It shares its vertex arrangement with the uniform compounds of 10 or 20 triangular prisms... 5/35|3 W83, U44, K49, C56 F 44=12{5}+12{5/2}+20{6} χ=-16	Rhombicosahedron Rhombicosahedron In geometry, the rhombicosahedron is a nonconvex uniform polyhedron, indexed as U56. Its vertex figure is an antiparallelogram.- Related polyhedra :... 2 35/2| W96, U56, K61, C72 F 50=30{4}+20{6} χ=-10
3.10/3.5/2.10/3 3.4*.-5/2.4* 10/3.4*.-10/3.4*	60	120	Ih	Great dodecicosidodecahedron Great dodecicosidodecahedron In geometry, the great dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U61.- Related polyhedra :It shares its vertex arrangement with the truncated great dodecahedron and the uniform compounds of 6 or 12 pentagonal prisms... 5/23|5/3 W99, U61, K66, C77 F 44=20{3}+12{5/2}+12{10/3 } χ=-16	Nonconvex great rhombicosidodecahedron (Quasirhombicosidodecahedron) 5/33|2 W105, U67, K72, C84 F 62=20{3}+30{4}+12{5/2} χ=2	Great rhombidodecahedron Great rhombidodecahedron In geometry, the great rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U73. Its vertex figure is a crossed quadrilateral.- Related polyhedra :... 2 3/25/3| W109, U73, K78, C89 F 42=30{4}+12{10/3} χ=-18
3.6.5/2.6 3.10*.-5/2.10* 6.10*.-6.10*	60	120	Ih	Small icosicosidodecahedron Small icosicosidodecahedron In geometry, the small icosicosidodecahedron is a nonconvex uniform polyhedron, indexed as U31.- Related polyhedra :It shares its vertex arrangement with the great stellated truncated dodecahedron... 5/23|3 W71, U31, K36, C40 F 52=20{3}+12{5/2}+20{6} χ=-8	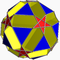Small ditrigonal dodecicosidodecahedron Small ditrigonal dodecicosidodecahedron In geometry, the small ditrigonal dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U43. Its vertex figure is a crossed quadrilateral.- Related polyhedra :It shares its vertex arrangement with the great stellated truncated dodecahedron... 5/33|5 W82, U43, K48, C55 F 44=20{3}+12{5/2}+12{10} χ=-16	Small dodecicosahedron Small dodecicosahedron In geometry, the small dodecicosahedron is a nonconvex uniform polyhedron, indexed as U50. Its vertex figure is a crossed quadrilateral.-Related polyhedra:It shares its vertex arrangement with the great stellated truncated dodecahedron... 3 3/2 5| W90, U50, K55, C64 F 32=20{6}+12{10} χ=-28
3.10/3.5.10/3 3.6*.-5.6* 10/3.6*.-10/3.6*	60	120	Ih	Great ditrigonal dodecicosidodecahedron Great ditrigonal dodecicosidodecahedron In geometry, the great ditrigonal dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U42.- Related polyhedra :It shares its vertex arrangement with the truncated dodecahedron... 3 5|5/3 W81, U42, K47, C54 F 44=20{3}+12{5}+12{10/3} χ=-16	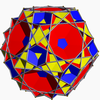Great icosicosidodecahedron Great icosicosidodecahedron In geometry, the great icosicosidodecahedron is a nonconvex uniform polyhedron, indexed as U48. Its vertex figure is a crossed quadrilateral.- Related polyhedra :It shares its vertex arrangement with the truncated dodecahedron... 3/25|3 W88, U48, K53, C62 F 52=20{3}+12{5}+20{6} χ=-8	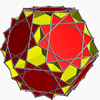Great dodecicosahedron Great dodecicosahedron In geometry, the great dodecicosahedron is a nonconvex uniform polyhedron, indexed as U63. Its vertex figure is a crossed quadrilateral.It has a composite Wythoff symbol, 3 5/3 |, requiring two different Schwarz triangles to generate it: and .Its vertex figure 6.10/3.6/5.10/7 is also ambiguous,... 3 5/35/2| W101, U63, K68, C79 F 32=20{6}+12{10/3} χ=-28