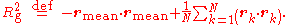Radius of gyration
Encyclopedia
Radius of gyration or gyradius is the name of several related measures of the size of an object, a surface, or an ensemble of points. It is calculated as the root mean square
distance of the objects' parts from either its center of gravity or an axis.
, the two-dimensional radius of gyration is used to describe the distribution of cross sectional
area in a column around its centroidal axis. The radius of gyration is given by the following formula
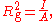
or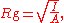
where I is the second moment of area
and A is the total cross-sectional area. The gyration radius is useful in estimating the stiffness of a column. However, if the principal moments of the two-dimensional gyration tensor are not equal, the column will tend to buckle
around the axis with the smaller principal moment. For example, a column with an elliptical
cross-section will tend to buckle in the direction of the smaller semiaxis.
It also can be referred to as the radial distance from a given axis at which the mass of a body could be concentrated without altering the rotational inertia of the body about that axis.
In engineering
, where people deal with continuous bodies of matter, the radius of gyration is usually calculated as an integral.
or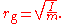
I is a scalar
, and is not the moment of inertia tensor
.
, the radius of gyration is used to describe the dimensions of a polymer
chain
. The radius of gyration of a particular molecule at a given time is defined as: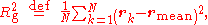
where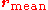
is the mean
position of the monomers.
As detailed below, the radius of gyration is also proportional to the root mean square distance between the monomers:
As a third method, the radius of gyration can also be computed by summing the principal moments of the gyration tensor.
Since the chain conformations
of a polymer sample are quasi infinite in number and constantly change over time, the "radius of gyration" discussed in polymer physics must usually be understood as a mean over all polymer molecules of the sample and over time. That is, the radius of gyration which is measured is an average over time or ensemble
:
where the angular brackets
denote the ensemble average
.
An entropically governed polymer chain (i.e. in so called theta conditions) follows a random walk in three dimensions. The radius of gyration for this case is given by
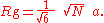
Note that although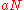
represents the contour length
of the polymer,
is strongly dependent of polymer stiffness and can vary over orders of magnitude. 
is reduced accordingly.
One reason that the radius of gyration is an interesting property is that it can be determined experimentally with static light scattering
as well as with small angle neutron-
and x-ray scattering
. This allows theoretical polymer physicists to check their models against reality.
The hydrodynamic radius
is numerically similar, and can be measured with Dynamic Light Scattering
(DLS).
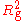are identical,
we first multiply out the summand in the first definition:
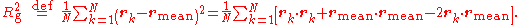
Carrying out the summation over the last two terms and using the definition of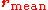
gives the formula
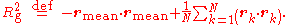
Root mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
distance of the objects' parts from either its center of gravity or an axis.
Applications in structural engineering
In structural engineeringStructural engineering
Structural engineering is a field of engineering dealing with the analysis and design of structures that support or resist loads. Structural engineering is usually considered a specialty within civil engineering, but it can also be studied in its own right....
, the two-dimensional radius of gyration is used to describe the distribution of cross sectional
Cross section (geometry)
In geometry, a cross-section is the intersection of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc...
area in a column around its centroidal axis. The radius of gyration is given by the following formula
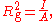
or
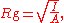
where I is the second moment of area
Second moment of area
The second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane...
and A is the total cross-sectional area. The gyration radius is useful in estimating the stiffness of a column. However, if the principal moments of the two-dimensional gyration tensor are not equal, the column will tend to buckle
Buckling
In science, buckling is a mathematical instability, leading to a failure mode.Theoretically, buckling is caused by a bifurcation in the solution to the equations of static equilibrium...
around the axis with the smaller principal moment. For example, a column with an elliptical
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
cross-section will tend to buckle in the direction of the smaller semiaxis.
It also can be referred to as the radial distance from a given axis at which the mass of a body could be concentrated without altering the rotational inertia of the body about that axis.
In engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, where people deal with continuous bodies of matter, the radius of gyration is usually calculated as an integral.
Applications in mechanics
The radius of gyration (r) about a given axis can be computed in terms of the mass moment of inertia I around that axis, and the total mass m;or
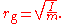
I is a scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
, and is not the moment of inertia tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
.
Molecular applications
In polymer physicsPolymer physics
Polymer physics is the field of physics that studies polymers, their fluctuations, mechanical properties, as well as the kinetics of reactions involving degradation and polymerisation of polymers and monomers respectively....
, the radius of gyration is used to describe the dimensions of a polymer
Polymer
A polymer is a large molecule composed of repeating structural units. These subunits are typically connected by covalent chemical bonds...
chain
Ideal chain
An ideal chain is the simplest model to describe a polymer. It only assumes a polymer as a random walk and neglects any kind of interactions among monomers...
. The radius of gyration of a particular molecule at a given time is defined as:
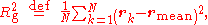
where
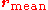is the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
position of the monomers.
As detailed below, the radius of gyration is also proportional to the root mean square distance between the monomers:
As a third method, the radius of gyration can also be computed by summing the principal moments of the gyration tensor.
Since the chain conformations
Chemical structure
A chemical structure includes molecular geometry, electronic structure and crystal structure of molecules. Molecular geometry refers to the spatial arrangement of atoms in a molecule and the chemical bonds that hold the atoms together. Molecular geometry can range from the very simple, such as...
of a polymer sample are quasi infinite in number and constantly change over time, the "radius of gyration" discussed in polymer physics must usually be understood as a mean over all polymer molecules of the sample and over time. That is, the radius of gyration which is measured is an average over time or ensemble
Ensemble average
In statistical mechanics, the ensemble average is defined as the mean of a quantity that is a function of the micro-state of a system , according to the distribution of the system on its micro-states in this ensemble....
:
where the angular brackets
denote the ensemble averageEnsemble average
In statistical mechanics, the ensemble average is defined as the mean of a quantity that is a function of the micro-state of a system , according to the distribution of the system on its micro-states in this ensemble....
.
An entropically governed polymer chain (i.e. in so called theta conditions) follows a random walk in three dimensions. The radius of gyration for this case is given by
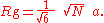
Note that although
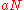represents the contour lengthContour length
Contour length is a term used in molecular physics. The contour length of a polymer chain is its length at maximum physically possible extension....
of the polymer,
is strongly dependent of polymer stiffness and can vary over orders of magnitude. is reduced accordingly.One reason that the radius of gyration is an interesting property is that it can be determined experimentally with static light scattering
Static light scattering
Static light scattering is a technique in physical chemistry that measures the intensity of the scattered light to obtain the average molecular weight Mw of a macromolecule like a polymer or a protein. Measurement of the scattering intensity at many angles allows calculation of the root mean square...
as well as with small angle neutron-
Small-angle neutron scattering
Small angle neutron scattering is a laboratory technique, similar to the often complementary techniques of small angle X-ray scattering and light scattering, used for investigations of structure of various substances, with spatial sensitivity of about 1 - 1000 nm...
and x-ray scattering
Small-angle X-ray scattering
Small-angle X-ray scattering is a small-angle scattering technique where the elastic scattering of X-rays by a sample which has inhomogeneities in the nm-range, is recorded at very low angles...
. This allows theoretical polymer physicists to check their models against reality.
The hydrodynamic radius
Hydrodynamic radius
The hydrodynamic radius of a macromolecule or colloid particle has two meanings. Some books use it as a synonym for the Stokes radius. Section 6.4 page 290....
is numerically similar, and can be measured with Dynamic Light Scattering
Dynamic light scattering
thumb|right|350px|Hypothetical Dynamic light scattering of two samples: Larger particles on the top and smaller particle on the bottomDynamic light scattering is a technique in physics that can be used to determine the size distribution profile of small particles in suspension or polymers...
(DLS).
Derivation of identity
To show that the two definitions of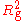 are identical,we first multiply out the summand in the first definition:
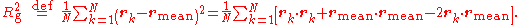
Carrying out the summation over the last two terms and using the definition of
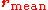gives the formula