
Cohomology ring
Encyclopedia
In mathematics
, specifically algebraic topology
, the cohomology ring of a topological space
X is a ring
formed from the cohomology
groups of X together with the cup product
serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is also present in other theories such as de Rham cohomology
. It is also functorial: for a continuous mapping of spaces one obtains a ring homomorphism
on cohomology rings, which is contravariant.
Specifically, given a sequence of cohomology groups Hk(X;R) on X with coefficients in a commutative ring
R (typically R is Zn, Z, Q, R, or C) one can define the cup product
, which takes the form
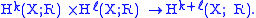
The cup product gives a multiplication on the direct sum
of the cohomology groups

This multiplication turns H•(X;R) into a ring. If fact, it is naturally an N-graded ring with the nonnegative integer k serving as the degree. The cup product respects this grading.
The cohomology ring is graded-commutative in the sense that the cup product commutes up to a sign determined by the grading. Specifically, for pure elements of degree k and ℓ we have
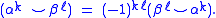
A numerical invariant derived from the cohomology ring is the cup-length, which means the maximum number of graded elements of degree ≥ 1, which when multiplied give a non-zero result. For example a complex projective space
has cup-length equal to its complex dimension
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the cohomology ring of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
formed from the cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
groups of X together with the cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is also present in other theories such as de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
. It is also functorial: for a continuous mapping of spaces one obtains a ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
on cohomology rings, which is contravariant.
Specifically, given a sequence of cohomology groups Hk(X;R) on X with coefficients in a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R (typically R is Zn, Z, Q, R, or C) one can define the cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
, which takes the form
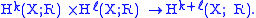
The cup product gives a multiplication on the direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of the cohomology groups

This multiplication turns H•(X;R) into a ring. If fact, it is naturally an N-graded ring with the nonnegative integer k serving as the degree. The cup product respects this grading.
The cohomology ring is graded-commutative in the sense that the cup product commutes up to a sign determined by the grading. Specifically, for pure elements of degree k and ℓ we have
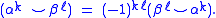
A numerical invariant derived from the cohomology ring is the cup-length, which means the maximum number of graded elements of degree ≥ 1, which when multiplied give a non-zero result. For example a complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
has cup-length equal to its complex dimension
Complex dimension
In mathematics, complex dimension usually refers to the dimension of a complex manifold M, or complex algebraic variety V. If the complex dimension is d, the real dimension will be 2d...
.

