
Andreotti–Frankel theorem
Encyclopedia
In mathematics
, the Andreotti–Frankel theorem from 1959 states that if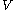 is a smooth affine variety of complex dimension
is a smooth affine variety of complex dimension
 or, more generally, if
or, more generally, if 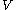 is any Stein manifold
is any Stein manifold
of dimension , then in fact
, then in fact 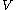 is homotopy equivalent to a CW complex
is homotopy equivalent to a CW complex
of real dimension at most n. In other words
 has only half as much topology.
has only half as much topology.
Consequently, if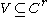 is a closed connected complex submanifold of complex dimension
is a closed connected complex submanifold of complex dimension  . Then
. Then 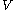 has the homotopy type of a
has the homotopy type of a 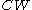 complex of real dimension
complex of real dimension 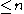 .
.
Therefore
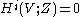 , for
, for 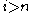
and
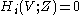 , for
, for 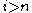 .
.
This theorem applies in particular to any smooth affine variety of dimension .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Andreotti–Frankel theorem from 1959 states that if
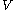 is a smooth affine variety of complex dimension
is a smooth affine variety of complex dimensionComplex dimension
In mathematics, complex dimension usually refers to the dimension of a complex manifold M, or complex algebraic variety V. If the complex dimension is d, the real dimension will be 2d...
 or, more generally, if
or, more generally, if 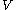 is any Stein manifold
is any Stein manifoldStein manifold
In mathematics, a Stein manifold in the theory of several complex variables and complex manifolds is a complex submanifold of the vector space of n complex dimensions. The name is for Karl Stein.- Definition :...
of dimension
 , then in fact
, then in fact 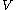 is homotopy equivalent to a CW complex
is homotopy equivalent to a CW complexCW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
of real dimension at most n. In other words
 has only half as much topology.
has only half as much topology.Consequently, if
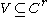 is a closed connected complex submanifold of complex dimension
is a closed connected complex submanifold of complex dimension  . Then
. Then 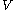 has the homotopy type of a
has the homotopy type of a 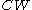 complex of real dimension
complex of real dimension 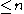 .
.Therefore
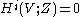 , for
, for 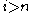
and
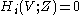 , for
, for 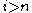 .
.This theorem applies in particular to any smooth affine variety of dimension
 .
.

