Daniell integral
Encyclopedia
In mathematics
, the Daniell integral is a type of integration that generalizes the concept of more elementary versions such as the Riemann integral
to which students are typically first introduced. One of the main difficulties with the traditional formulation of the Lebesgue integral is that it requires the initial development of a workable measure theory before any useful results for the integral can be obtained. However, an alternative approach is available, developed by that does not suffer from this deficiency, and has a few significant advantages over the traditional formulation, especially as the integral is generalized into higher dimensional spaces and further generalizations such as the Stieltjes integral. The basic idea involves the axiomatization of the integral.
of bounded real functions (called elementary functions) defined over some set 
, that satisfies these two axioms:
In addition, every function h in H is assigned a real number
, which is called the elementary integral of h, satisfying these three axioms:
That is, we define a continuous non-negative linear functional
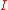over the space of elementary functions.
These elementary functions and their elementary integrals may be any set of functions and definitions of integrals over these functions which satisfy these axioms. The family of all step function
s evidently satisfies the above axioms for elementary functions. Defining the elementary integral of the family of step functions as the (signed) area underneath a step function evidently satisfies the given axioms for an elementary integral. Applying the construction of the Daniell integral described further below using step functions as elementary functions produces a definition of an integral equivalent to the Lebesgue integral. Using the family of all continuous function
s as the elementary functions and the traditional Riemann integral
as the elementary integral is also possible, however, this will yield an integral that is also equivalent to Lebesgue's definition. Doing the same, but using the Riemann–Stieltjes integral, along with an appropriate function of bounded variation
, gives a definition of integral equivalent to the Lebesgue–Stieltjes integral.
Sets of measure zero may be defined in terms of elementary functions as follows. A set
which is a subset of 
is a set of measure zero if for any 
, there exists a nondecreasing sequence of nonnegative elementary functions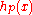 
in H such that 
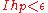and 
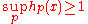on 
.
A set is called a set of full measure if its complement, relative to
, is a set of measure zero. We say that if some property holds at every point of a set of full measure (or equivalently everywhere except on a set of measure zero), it holds almost everywhere
.
, which is the family of all functions that are the limit of a nondecreasing sequence 
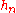of elementary functions almost everywhere, such that the set of integrals 
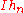is bounded. The integral of a function 
in 
is defined as:
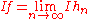
It can be shown that this definition of the integral is well-defined, i.e. it does not depend on the choice of sequence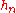
.
However, the class
is in general not closed under subtraction and scalar multiplication by negative numbers, but we can further extend it by defining a wider class of functions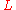 
such that every function 
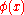can be represented on a set of full measure as the difference 
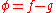, for some functions 
and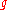 
in the class 
. Then the integral of a function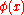 
can be defined as:
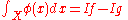
Again, it may be shown that this integral is well-defined, i.e. it does not depend on the decomposition of
into 
and 
. This is the final construction of the Daniell integral.
, Fatou's lemma
, and Fubini's theorem
may also readily be proved using this construction. Its properties are identical to the traditional Lebesgue integral.
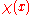of some set, then its integral may be taken as the measure of the set. This definition of measure based on the Daniell integral can be shown to be equivalent to the traditional Lebesgue measure
.
. The Lebesgue and Daniell constructions are equivalent, as pointed out above, if ordinary finite-valued step functions are chosen as elementary functions. However, as one tries to extend the definition of the integral into more complex domains (e.g. attempting to define the integral of a linear functional
), one runs into practical difficulties using Lebesgue's construction that are alleviated with the Daniell approach.
The Polish mathematician Jan Mikusinski
has made an alternative and more natural formulation of Daniell integration by using the notion of absolutely convergent series. His formulation works for
Bochner integral
(Lebesgue integral for mappings taking values in Banach space
s). Mikusinski's lemma allows one to define integral without mentioning null set
s. He also proved change of variables theorem for multiple integral for Bochner integrals and Fubini's theorem for Bochner integrals using Daniell integration. The book by Asplund and Bungart carries a lucid treatment of this approach for real valued functions. It also offers a proof of an abstract Radon–Nikodym theorem
using Daniell–Mikusinski approach.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Daniell integral is a type of integration that generalizes the concept of more elementary versions such as the Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
to which students are typically first introduced. One of the main difficulties with the traditional formulation of the Lebesgue integral is that it requires the initial development of a workable measure theory before any useful results for the integral can be obtained. However, an alternative approach is available, developed by that does not suffer from this deficiency, and has a few significant advantages over the traditional formulation, especially as the integral is generalized into higher dimensional spaces and further generalizations such as the Stieltjes integral. The basic idea involves the axiomatization of the integral.
The Daniell axioms
We start by choosing a family of bounded real functions (called elementary functions) defined over some set , that satisfies these two axioms:- 1.
is a linear space with the usual operations of addition and scalar multiplication. - 2. If a function
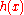is in 
, so is its absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
.
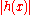In addition, every function h in H is assigned a real number
, which is called the elementary integral of h, satisfying these three axioms:- 1. Linearity. If h and k are both in H, and
and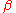 
are any two real numbers, then 
. - 2. Nonnegativity. If
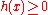, then 
. - 3. Continuity. If
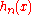is a nonincreasing sequence (i.e. 
) of functions in 
that converges to 0 for all 
in 
, then 
.
That is, we define a continuous non-negative linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
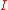over the space of elementary functions.These elementary functions and their elementary integrals may be any set of functions and definitions of integrals over these functions which satisfy these axioms. The family of all step function
Step function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals...
s evidently satisfies the above axioms for elementary functions. Defining the elementary integral of the family of step functions as the (signed) area underneath a step function evidently satisfies the given axioms for an elementary integral. Applying the construction of the Daniell integral described further below using step functions as elementary functions produces a definition of an integral equivalent to the Lebesgue integral. Using the family of all continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s as the elementary functions and the traditional Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
as the elementary integral is also possible, however, this will yield an integral that is also equivalent to Lebesgue's definition. Doing the same, but using the Riemann–Stieltjes integral, along with an appropriate function of bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
, gives a definition of integral equivalent to the Lebesgue–Stieltjes integral.
Sets of measure zero may be defined in terms of elementary functions as follows. A set
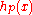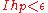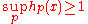which is a subset of is a set of measure zero if for any , there exists a nondecreasing sequence of nonnegative elementary functions in H such that and on .A set is called a set of full measure if its complement, relative to
, is a set of measure zero. We say that if some property holds at every point of a set of full measure (or equivalently everywhere except on a set of measure zero), it holds almost everywhereAlmost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
.
Definition of the Daniell integral
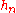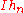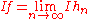
We can then proceed to define a larger class of functions, based on our chosen elementary functions, the class, which is the family of all functions that are the limit of a nondecreasing sequence of elementary functions almost everywhere, such that the set of integrals is bounded. The integral of a function in is defined as:It can be shown that this definition of the integral is well-defined, i.e. it does not depend on the choice of sequence
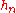.However, the class
is in general not closed under subtraction and scalar multiplication by negative numbers, but we can further extend it by defining a wider class of functions 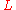such that every function 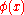can be represented on a set of full measure as the difference 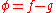, for some functions and 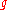in the class . Then the integral of a function 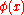can be defined as: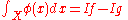Again, it may be shown that this integral is well-defined, i.e. it does not depend on the decomposition of
into and . This is the final construction of the Daniell integral.Properties
Nearly all of the important theorems in the traditional theory of the Lebesgue integral, such as Lebesgue's dominated convergence theorem, the Riesz–Fischer theoremRiesz–Fischer theorem
In mathematics, the Riesz–Fischer theorem in real analysis refers to a number of closely related results concerning the properties of the space L2 of square integrable functions...
, Fatou's lemma
Fatou's lemma
In mathematics, Fatou's lemma establishes an inequality relating the integral of the limit inferior of a sequence of functions to the limit inferior of integrals of these functions...
, and Fubini's theorem
Fubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
may also readily be proved using this construction. Its properties are identical to the traditional Lebesgue integral.
Measures from the Daniell integral
Because of the natural correspondence between sets and functions, it is also possible to use the Daniell integral to construct a measure theory. If we take the characteristic functionCharacteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
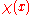of some set, then its integral may be taken as the measure of the set. This definition of measure based on the Daniell integral can be shown to be equivalent to the traditional Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
.
Advantages over the traditional formulation
This method of constructing the general integral has a few advantages over the traditional method of Lebesgue, particularly in the field of functional analysisFunctional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. The Lebesgue and Daniell constructions are equivalent, as pointed out above, if ordinary finite-valued step functions are chosen as elementary functions. However, as one tries to extend the definition of the integral into more complex domains (e.g. attempting to define the integral of a linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
), one runs into practical difficulties using Lebesgue's construction that are alleviated with the Daniell approach.
The Polish mathematician Jan Mikusinski
Jan Mikusinski
Prof. Jan Mikusiński was a Polish mathematician known for his pioneering work in mathematical analysis. Mikusiński developed an operational calculus - 44A40 Calculus of Mikusiński, which is relevant for solving differential equations...
has made an alternative and more natural formulation of Daniell integration by using the notion of absolutely convergent series. His formulation works for
Bochner integral
Bochner integral
In mathematics, the Bochner integral, named for Salomon Bochner, extends the definition of Lebesgue integral to functions that take values in a Banach space, as the limit of integrals of simple functions.-Definition:...
(Lebesgue integral for mappings taking values in Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s). Mikusinski's lemma allows one to define integral without mentioning null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
s. He also proved change of variables theorem for multiple integral for Bochner integrals and Fubini's theorem for Bochner integrals using Daniell integration. The book by Asplund and Bungart carries a lucid treatment of this approach for real valued functions. It also offers a proof of an abstract Radon–Nikodym theorem
Radon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
using Daniell–Mikusinski approach.