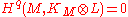Kodaira vanishing theorem
Encyclopedia
In mathematics
, the Kodaira vanishing theorem is a basic result of complex manifold
theory and complex algebraic geometry
, describing general conditions under which sheaf cohomology
groups with indices q > 0 are automatically zero. The implications for the group with index q = 0 is usually that its dimension — the number of independent global sections — coincides with a holomorphic Euler characteristic that can be computed using the Hirzebruch-Riemann-Roch theorem
.
of complex dimension n, L any holomorphic line bundle on M that is a positive line bundle
, and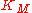 is the canonical line bundle
is the canonical line bundle
, then
for q > 0. Here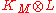 stands for the tensor product of line bundles. By means of Serre duality
stands for the tensor product of line bundles. By means of Serre duality
, one obtains the vanishing of other cohomology group by removing K.
There is a generalisation, the Kodaira-Nakano vanishing theorem, in which , where
, where  denotes the sheaf of holomorphic (n,0)-forms on M with values on L, is replaced by
denotes the sheaf of holomorphic (n,0)-forms on M with values on L, is replaced by 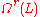 , the sheaf of holomorphic (r,0)-forms with values on L. Then the cohomology group
, the sheaf of holomorphic (r,0)-forms with values on L. Then the cohomology group 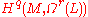 vanishes whenever
vanishes whenever
being ample
(i.e., some tensor power gives a projective embedding). The algebraic Kodaira-Akizuki-Nakano vanishing theorem is the following statement:
showed that this result does not always hold over fields of characteristic p > 0, and in particular fails for Raynaud surface
s.
Until 1987 the only known proof in characteristic zero was however based on the complex analytic proof and the GAGA
comparison theorems. However, in 1987 Pierre Deligne
and Luc Illusie
gave a purely algebraic proof of the vanishing theorem in . Their proof is based on showing that Hodge-de Rham spectral sequence for algebraic de Rham cohomology degenerates in degree 1. It is remarkable that this is shown by lifting a corresponding more specific result from characteristic p > 0 — the positive-characteristic result does not hold without limitations but can be lifted to provide the full result.
was derived with the help of the vanishing theorem. With application of Serre's duality, the vanishing of various sheaf cohomology groups (usually related to the canonical line bundle) of curves and surfaces help with the classification of complex manifolds, e.g. Enriques–Kodaira classification.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Kodaira vanishing theorem is a basic result of complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
theory and complex algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, describing general conditions under which sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
groups with indices q > 0 are automatically zero. The implications for the group with index q = 0 is usually that its dimension — the number of independent global sections — coincides with a holomorphic Euler characteristic that can be computed using the Hirzebruch-Riemann-Roch theorem
Hirzebruch-Riemann-Roch theorem
In mathematics, the Hirzebruch–Riemann–Roch theorem, named after Friedrich Hirzebruch, Bernhard Riemann, and Gustav Roch, is Hirzebruch's 1954 result contributing to the Riemann–Roch problem for complex algebraic varieties of all dimensions...
.
The complex analytic case
The statement of Kunihiko Kodaira's result is that if M is a compact Kähler manifoldKähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
of complex dimension n, L any holomorphic line bundle on M that is a positive line bundle
Positive form
In complex geometry, the term positive formrefers to several classes of real differential formsof Hodge type .- -forms :Real -forms on a complex manifold Mare forms which are of type and real,...
, and
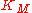 is the canonical line bundle
is the canonical line bundleCanonical line bundle
The canonical or tautological line bundle on a projective space appears frequently in mathematics, often in the study of characteristic classes...
, then
for q > 0. Here
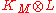 stands for the tensor product of line bundles. By means of Serre duality
stands for the tensor product of line bundles. By means of Serre dualitySerre duality
In algebraic geometry, a branch of mathematics, Serre duality is a duality present on non-singular projective algebraic varieties V of dimension n . It shows that a cohomology group Hi is the dual space of another one, Hn−i...
, one obtains the vanishing of other cohomology group by removing K.
There is a generalisation, the Kodaira-Nakano vanishing theorem, in which
 , where
, where  denotes the sheaf of holomorphic (n,0)-forms on M with values on L, is replaced by
denotes the sheaf of holomorphic (n,0)-forms on M with values on L, is replaced by 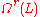 , the sheaf of holomorphic (r,0)-forms with values on L. Then the cohomology group
, the sheaf of holomorphic (r,0)-forms with values on L. Then the cohomology group 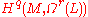 vanishes whenever
vanishes whenever- q + r > n.
The algebraic case
The Kodaira vanishing theorem can be formulated within the language of algebraic geometry without any reference to transcendental methods such as Kähler metrics. Positivity of the line bundle L translates into the corresponding invertible sheafInvertible sheaf
In mathematics, an invertible sheaf is a coherent sheaf S on a ringed space X, for which there is an inverse T with respect to tensor product of OX-modules. It is the equivalent in algebraic geometry of the topological notion of a line bundle...
being ample
Ample line bundle
In algebraic geometry, a very ample line bundle is one with enough global sections to set up an embedding of its base variety or manifold M into projective space. An ample line bundle is one such that some positive power is very ample...
(i.e., some tensor power gives a projective embedding). The algebraic Kodaira-Akizuki-Nakano vanishing theorem is the following statement:
- If k is a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero, X is a smooth and projective k-schemeScheme (mathematics)In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
of dimension d, and L is an ample invertible sheaf on X, then-
 for
for 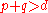 , and
, and for
for 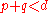 ,
,
-
- where the Ωp denote the sheavesSheaf (mathematics)In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of relative (algebraic) differential forms (see Kähler differentialKähler differentialIn mathematics, Kähler differentials provide an adaptation of differential forms to arbitrary commutative rings or schemes.-Presentation:The idea was introduced by Erich Kähler in the 1930s...
).
showed that this result does not always hold over fields of characteristic p > 0, and in particular fails for Raynaud surface
Raynaud surface
In mathematics, a Raynaud surface is a particular kind of algebraic surface that was introduced in and named for . To be precise, a Raynaud surface is a quasi-elliptic surface over an algebraic curve of genus g greater than 1, such that all fibers are irreducible and the fibration has a section...
s.
Until 1987 the only known proof in characteristic zero was however based on the complex analytic proof and the GAGA
Gaga
- Entertainment :* Lady Gaga , American recording artist* Gaga , a dancing technique* Rara, a type of Caribbean music called Gaga in the Dominican Republic* GNZ-004 Gaga, a mobile weapon in Mobile Suit Gundam 00- Sports :...
comparison theorems. However, in 1987 Pierre Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
and Luc Illusie
Luc Illusie
Luc Illusie is a French mathematician. He is a former student of École Normale Supérieure, and got his PhD under the supervision of Alexander Grothendieck. He is professor emeritus at the Paris-Sud 11 University. Illusie made notable contributions to algebraic geometry.-External links:*...
gave a purely algebraic proof of the vanishing theorem in . Their proof is based on showing that Hodge-de Rham spectral sequence for algebraic de Rham cohomology degenerates in degree 1. It is remarkable that this is shown by lifting a corresponding more specific result from characteristic p > 0 — the positive-characteristic result does not hold without limitations but can be lifted to provide the full result.
Consequences and applications
Historically, Kodaira embedding theoremKodaira embedding theorem
In mathematics, the Kodaira embedding theorem characterises non-singular projective varieties, over the complex numbers, amongst compact Kähler manifolds...
was derived with the help of the vanishing theorem. With application of Serre's duality, the vanishing of various sheaf cohomology groups (usually related to the canonical line bundle) of curves and surfaces help with the classification of complex manifolds, e.g. Enriques–Kodaira classification.
See also
- Kawamata–Viehweg vanishing theoremKawamata–Viehweg vanishing theoremIn algebraic geometry, the Kawamata–Viehweg vanishing theorem is an extension of the Kodaira vanishing theorem, on the vanishing of coherent cohomology groups, to logarithmic pairs, proved independently by and ....
- Mumford vanishing theorem
- Ramanujam vanishing theoremRamanujam vanishing theoremIn algebraic geometry, the Ramanujam vanishing theorem is an extension of the Kodaira vanishing theorem due to , that in particular gives conditions for the vanishing of first cohomology groups of coherent sheaves on a surface...