
Positive form
Encyclopedia
In complex geometry
, the term positive form
refers to several classes of real differential forms
of Hodge type (p, p).
are forms which are of type (p,p) and real,
that is, lie in the intersection
A real (1,1)-form
is called positive if any of the
following equivalent conditions hold
forms of ample line bundle
s (also known as
positive line bundles). Let L be a holomorphic Hermitian line
bundle on a complex manifold,
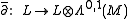
its complex structure operator. Then L is equipped with a unique connection preserving the Hermitian structure and satisfying
 .
.
This connection is called the Chern connection
.
The curvature of a Chern connection is always a
of a Chern connection is always a
purely imaginary (1,1)-form. A line bundle L is called positive if

is a positive definite (1,1)-form. The Kodaira embedding theorem
claims that a positive line bundle is ample, and conversely, any ample line bundle
admits a Hermitian metric with positive.
positive.
.
When M is a compact complex surface,
 , this cone is
, this cone is
self-dual, with respect
to the Poincaré pairing
For (p, p)-forms, where ,
,
there are two different notions of positivity. A form is called
strongly positive if it is a linear combination of
products of positive forms, with positive real coefficients.
A real (p, p)-form on an n-dimensional
on an n-dimensional
complex manifold M is called weakly positive
if for all strongly positive (n-p, n-p)-forms
ζ with compact support, we have
 .
.
Weakly positive and strongly positive forms
form convex cones. On compact manifolds
these cones are dual
with respect to the Poincaré pairing.
Complex geometry
In mathematics, complex geometry is the study of complex manifolds and functions of many complex variables. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric chapters of complex analysis....
, the term positive form
refers to several classes of real differential forms
of Hodge type (p, p).
(1,1)-forms
Real (p,p)-forms on a complex manifold Mare forms which are of type (p,p) and real,
that is, lie in the intersection

A real (1,1)-form

is called positive if any of the
following equivalent conditions hold
 is an imaginary part of a positive (not necessarily positive definite) Hermitian form.
is an imaginary part of a positive (not necessarily positive definite) Hermitian form.- For some basis
 in the space
in the space  of (1,0)-forms,
of (1,0)-forms, can be written diagonally, as
can be written diagonally, as 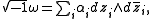 with
with 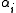 real and non-negative.
real and non-negative. - For any (1,0)-tangent vector
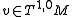 ,
, 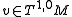
- For any real tangent vector
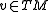 ,
, 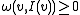 , where
, where 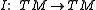 is the complex structure operator.
is the complex structure operator.
Positive line bundles
In algebraic geometry, positive (1,1)-forms arise as curvatureforms of ample line bundle
Ample line bundle
In algebraic geometry, a very ample line bundle is one with enough global sections to set up an embedding of its base variety or manifold M into projective space. An ample line bundle is one such that some positive power is very ample...
s (also known as
positive line bundles). Let L be a holomorphic Hermitian line
bundle on a complex manifold,
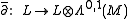
its complex structure operator. Then L is equipped with a unique connection preserving the Hermitian structure and satisfying
 .
.This connection is called the Chern connection
Hermitian connection
In mathematics, the Hermitian connection \nabla, also called the Chern connection, is the unique connection on a Hermitian manifold that satisfies the following conditions,# It preserves the metric g, i.e., \nabla g=0....
.
The curvature
 of a Chern connection is always a
of a Chern connection is always apurely imaginary (1,1)-form. A line bundle L is called positive if

is a positive definite (1,1)-form. The Kodaira embedding theorem
Kodaira embedding theorem
In mathematics, the Kodaira embedding theorem characterises non-singular projective varieties, over the complex numbers, amongst compact Kähler manifolds...
claims that a positive line bundle is ample, and conversely, any ample line bundle
Ample line bundle
In algebraic geometry, a very ample line bundle is one with enough global sections to set up an embedding of its base variety or manifold M into projective space. An ample line bundle is one such that some positive power is very ample...
admits a Hermitian metric with
 positive.
positive.Positivity for (p, p)-forms
Positive (1,1)-forms on M form a convex coneConvex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
.
When M is a compact complex surface,
 , this cone is
, this cone isself-dual, with respect
to the Poincaré pairing

For (p, p)-forms, where
 ,
,there are two different notions of positivity. A form is called
strongly positive if it is a linear combination of
products of positive forms, with positive real coefficients.
A real (p, p)-form
 on an n-dimensional
on an n-dimensionalcomplex manifold M is called weakly positive
if for all strongly positive (n-p, n-p)-forms
ζ with compact support, we have
 .
.Weakly positive and strongly positive forms
form convex cones. On compact manifolds
these cones are dual
with respect to the Poincaré pairing.

