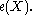Random compact set
Encyclopedia
In mathematics
, a random compact set is essentially a compact set
-valued random variable
. Random compact sets are useful in the study of attractors for random dynamical system
s.
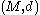be a complete
separable metric space
. Let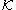
denote the set of all compact subsets of 
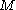. The Hausdorff metric 
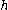on 
is defined by
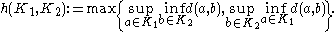
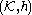is also а complete separable metric space. The corresponding open subsets generate a σ-algebra on 
, the Borel sigma algebra 
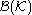of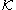 
.
A random compact set is а measurable function
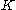from а probability space
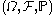into 
.
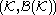Put another way, a random compact set is a measurable function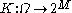
such that 
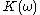is almost surely
compact and
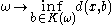
is a measurable function for every
.
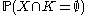for 
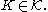
(The distribution of а random compact convex set is also given by the system of all inclusion probabilities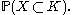
)
For
, the probability 
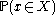is obtained, which satisfies
Thus the covering function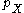
is given by
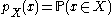for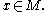 
Of course,
can also be interpreted as the mean of the indicator function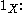 
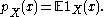
The covering function takes values between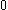
and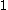 
. The set 
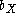of all 
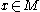with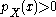 
is called the support of 
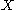. The set 
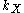, of all 
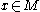with 
is called the kernel, the set of fixed points, or essential minimum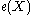 
. If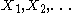 
, is а sequence of i.i.d. random compact sets, then almost surely
and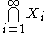
converges almost surely to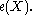 
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a random compact set is essentially a compact set
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
-valued random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
. Random compact sets are useful in the study of attractors for random dynamical system
Random dynamical system
In mathematics, a random dynamical system is a measure-theoretic formulation of a dynamical system with an element of "randomness", such as the dynamics of solutions to a stochastic differential equation...
s.
Definition
Let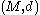 be a completeComplete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
separable metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. Let
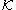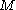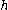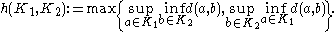
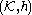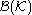denote the set of all compact subsets of . The Hausdorff metric on is defined by is also а complete separable metric space. The corresponding open subsets generate a σ-algebra on , the Borel sigma algebra of 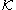.A random compact set is а measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
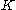from а probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
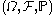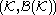into .Put another way, a random compact set is a measurable function
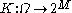such that 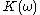is almost surelyAlmost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
compact and
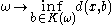
is a measurable function for every
.Discussion
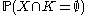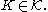
Random compact sets in this sense are also random closed sets as in Matheron (1975). Consequently their distribution is given by the probabilities for (The distribution of а random compact convex set is also given by the system of all inclusion probabilities
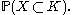)For
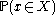, the probability is obtained, which satisfiesThus the covering function
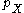is given by 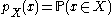for 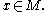Of course,
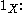
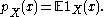
can also be interpreted as the mean of the indicator function The covering function takes values between
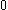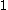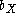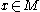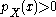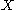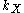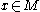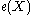and . The set of all with is called the support of . The set , of all with is called the kernel, the set of fixed points, or essential minimum . If 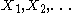, is а sequence of i.i.d. random compact sets, then almost surelyand
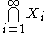converges almost surely to