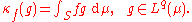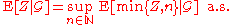Hölder's inequality
Encyclopedia
In mathematical analysis
Hölder's inequality, named after Otto Hölder
, is a fundamental inequality between integrals
and an indispensable tool for the study of Lp spaces
.
Let (S, Σ, μ) be a measure space and let 1 ≤ p, q ≤ ∞ with 1/p + 1/q = 1. Then, for all measurable
real
- or complex
-valued functions
f and g on S,
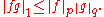
The numbers p and q above are said to be Hölder conjugates of each other. The special case p = q = 2 gives a form of the Cauchy–Schwarz inequality
.
Hölder's inequality holds even if ||fg ||1 is infinite, the right-hand side also being infinite in that case. In particular, if f is in Lp(μ) and g is in Lq(μ), then fg is in L1(μ).
For 1 < p, q < ∞ and f ∈ Lp(μ) and g ∈ Lq(μ), Hölder's inequality becomes an equality if and only if |f |p and |g |q are linearly dependent in L1(μ), meaning that there exist real numbers α, β ≥ 0, not both of them zero, such that α |f |p = β |g |q μ-almost everywhere
.
Hölder's inequality is used to prove the Minkowski inequality
, which is the triangle inequality
in the space Lp(μ), and also to establish that Lq(μ) is the dual space
of Lp(μ) for 1 ≤ p < ∞.
Hölder's inequality was first found by , and discovered independently by .
function, respectively, are μ-integrable, the estimates

and the similar one for fg hold, and Hölder's inequality can be applied to the right-hand side. In particular, if f and g are in the Hilbert space
L2(μ), then Hölder's inequality for p = q = 2 implies

where the angle brackets refer to the inner product of L2(μ). This is also called Cauchy–Schwarz inequality
, but requires for its statement that ||f ||2 and ||g ||2 are finite to make sure that the inner product of f and g is well defined.
, then 1 ≤ p, q ≤ ∞ just need to satisfy 1/p + 1/q ≤ 1, rather than being Hölder conjugates. A combination of Hölder's inequality and Jensen's inequality
implies that
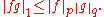
for all measurable real- or complex-valued functions f and g on S,
, when the set S is {1, …, n} with the counting measure
, we have
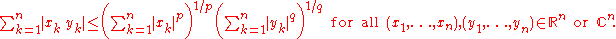
If S = N with the counting measure, then we get Hölder's inequality for sequence space
s:
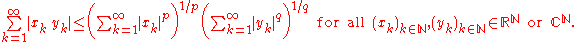
, and f and g are measurable real- or complex-valued functions on S, then Hölder inequality is
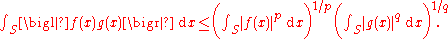
 , let E denote the expectation operator
, let E denote the expectation operator
. For real- or complex-valued random variable
s X and Y on Ω, Hölder's inequality reads
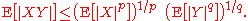
Let 0 < r < s and define . Then is the Hölder conjugate of p. Applying Hölder's inequality to the random variables |X |r and 1Ω, we obtain

In particular, if the sth absolute moment
is finite, then the r th absolute moment is finite, too. (This also follows from Jensen's inequality
.)
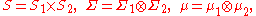
where S is the Cartesian product
of S1 and S2, the σ-algebra Σ arises as product σ-algebra of Σ1 and Σ2, and μ denotes the product measure
of μ1 and μ2. Then Tonelli's theorem allows us to rewrite Hölder's inequality using iterated integrals: If f and g are real- or complex-valued functions on the Cartesian product S, then

This can be generalized to more than two σ-finite measure spaces.
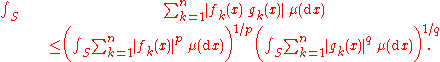
This generalizes to functions f and g taking values in a sequence space
.
.
If ||f ||p = 0, then f is zero μ-almost everywhere, and the product fg is zero μ-almost everywhere, hence the left-hand side of Hölder's inequality is zero. The same is true if ||g ||q = 0. Therefore, we may assume ||f ||p > 0 and ||g ||q > 0 in the following.
If ||f ||p = ∞ or ||g ||q = ∞, then the right-hand side of Hölder's inequality is infinite. Therefore, we may assume that ||f ||p and ||g ||q are in (0, ∞).
If p = ∞ and q = 1, then |fg | ≤ ||f ||∞ |g | almost everywhere and Hölders inequality follows from the monotonicity of the Lebesgue integral. Similarly for p = 1 and q = ∞. Therefore, we may also assume p, q ∈ (1, ∞).
Dividing f and g by ||f ||p and ||g ||q, respectively, we can assume that
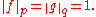
We now use Young's inequality, which states that
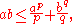
for all nonnegative a and b, where equality is achieved if and only if a p = b q. Hence
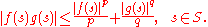
Integrating both sides gives
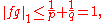
which proves the claim.
Under the assumptions p ∈ (1, ∞) and ||f ||p = ||g ||q = 1, equality holds if and only if |f |p = |g |q almost everywhere. More generally, if ||f ||p and ||g ||q are in (0, ∞), then Hölder's inequality becomes an equality if and only if there exist real numbers α, β > 0, namely
 and
and 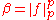
such that
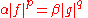 μ-almost everywhere (*)
μ-almost everywhere (*)
The case ||f ||p = 0 corresponds to β = 0 in (*). The case ||g ||q = 0 corresponds to α = 0 in (*).
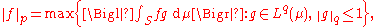
where max indicates that there actually is a g maximizing the right-hand side. When p = ∞ and if each set A in the σ-field Σ with μ(A) = ∞ contains a subset B ∈ Σ with 0 < μ(B) < ∞ (which is true in particular when μ is σ-finite), then
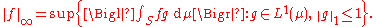
] such that
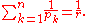
Then, for all measurable real- or complex-valued functions f1, …, fn defined on S,
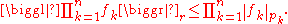
In particular,
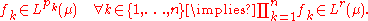
Note:
] and let θ1, …, θn ∈ (0, 1) denote weights with θ1+ … + θn = 1. Define p as the weighted harmonic mean
, i.e.,
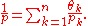
Given a measurable real- or complex-valued functions f on S, define
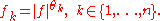
Then by the above generalization of Hölder's inequality,
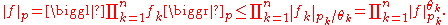
As an interpolation
result for n = 2,

where θ ∈ (0, 1) and
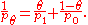
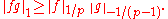
If ||fg ||1 < ∞ and ||g ||−1/(p −1) > 0, then the reverse Hölder inequality is an equality if and only if there exists an α ≥ 0 such that
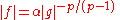 μ-almost everywhere.
μ-almost everywhere.
Note: ||f ||1/p and ||g ||−1/(p −1) are not norms, these expressions are just compact notation for
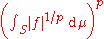 and
and 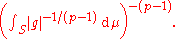
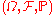 be a probability space,
be a probability space,  a sub-σ-algebra, and p, q ∈ (1, ∞) Hölder conjugates, meaning that 1/p + 1/q = 1. Then, for all real- or complex-valued random variables X and Y on Ω,
a sub-σ-algebra, and p, q ∈ (1, ∞) Hölder conjugates, meaning that 1/p + 1/q = 1. Then, for all real- or complex-valued random variables X and Y on Ω,
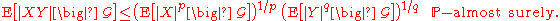
Remarks:
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
Hölder's inequality, named after Otto Hölder
Otto Hölder
Otto Ludwig Hölder was a German mathematician born in Stuttgart.Hölder first studied at the Polytechnikum and then in 1877 went to Berlin where he was a student of Leopold Kronecker, Karl Weierstraß, and Ernst Kummer.He is famous for many things including: Hölder's inequality, the Jordan–Hölder...
, is a fundamental inequality between integrals
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
and an indispensable tool for the study of Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
.
Let (S, Σ, μ) be a measure space and let 1 ≤ p, q ≤ ∞ with 1/p + 1/q = 1. Then, for all measurable
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
- or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f and g on S,
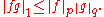
The numbers p and q above are said to be Hölder conjugates of each other. The special case p = q = 2 gives a form of the Cauchy–Schwarz inequality
Cauchy–Schwarz inequality
In mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
.
Hölder's inequality holds even if ||fg ||1 is infinite, the right-hand side also being infinite in that case. In particular, if f is in Lp(μ) and g is in Lq(μ), then fg is in L1(μ).
For 1 < p, q < ∞ and f ∈ Lp(μ) and g ∈ Lq(μ), Hölder's inequality becomes an equality if and only if |f |p and |g |q are linearly dependent in L1(μ), meaning that there exist real numbers α, β ≥ 0, not both of them zero, such that α |f |p = β |g |q μ-almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
.
Hölder's inequality is used to prove the Minkowski inequality
Minkowski inequality
In mathematical analysis, the Minkowski inequality establishes that the Lp spaces are normed vector spaces. Let S be a measure space, let 1 ≤ p ≤ ∞ and let f and g be elements of Lp...
, which is the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
in the space Lp(μ), and also to establish that Lq(μ) is the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of Lp(μ) for 1 ≤ p < ∞.
Hölder's inequality was first found by , and discovered independently by .
Conventions
The brief statement of Hölder's inequality uses some conventions.- In the definition of Hölder conjugates, 1/ ∞ means zero.
- If 1 ≤ p, q < ∞, then ||f ||p and ||g ||q stand for the (possibly infinite) expressions
-
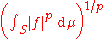 and
and 
- If p = ∞, then ||f ||∞ stands for the essential supremum of |f |, similarly for ||g ||∞.
- The notation ||f ||p with 1 ≤ p ≤ ∞ is a slight abuse, because in general it is only a normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of f if ||f ||p is finite and f is considered as equivalence class of μ-almost everywhere equal functions. If f ∈ Lp(μ) and g ∈ Lq(μ), then the notation is adequate.
- On the right-hand side of Hölder's inequality, 0 times ∞ as well as ∞ times 0 means 0. Multiplying a > 0 with ∞ gives ∞.
Estimates for integrable products
As above, let f and g denote measurable real- or complex-valued functions defined on S. If ||fg ||1 is finite, then the products of f with g and its complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
function, respectively, are μ-integrable, the estimates

and the similar one for fg hold, and Hölder's inequality can be applied to the right-hand side. In particular, if f and g are in the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
L2(μ), then Hölder's inequality for p = q = 2 implies

where the angle brackets refer to the inner product of L2(μ). This is also called Cauchy–Schwarz inequality
Cauchy–Schwarz inequality
In mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
, but requires for its statement that ||f ||2 and ||g ||2 are finite to make sure that the inner product of f and g is well defined.
Generalization for probability measures
If (S, Σ, μ) is a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, then 1 ≤ p, q ≤ ∞ just need to satisfy 1/p + 1/q ≤ 1, rather than being Hölder conjugates. A combination of Hölder's inequality and Jensen's inequality
Jensen's inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...
implies that
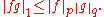
for all measurable real- or complex-valued functions f and g on S,
Notable special cases
For the following cases assume that p and q are in the open interval (1, ∞) with 1/p + 1/q = 1.Counting measure
In the case of n-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, when the set S is {1, …, n} with the counting measure
Counting measure
In mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
, we have
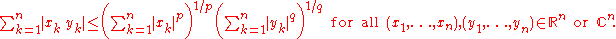
If S = N with the counting measure, then we get Hölder's inequality for sequence space
Sequence space
In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...
s:
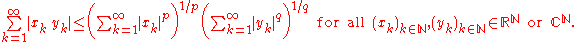
Lebesgue measure
If S is a measurable subset of Rn with the Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
, and f and g are measurable real- or complex-valued functions on S, then Hölder inequality is
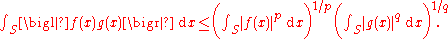
Probability measure
For the probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
 , let E denote the expectation operator
, let E denote the expectation operatorExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
. For real- or complex-valued random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X and Y on Ω, Hölder's inequality reads
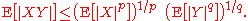
Let 0 < r < s and define . Then is the Hölder conjugate of p. Applying Hölder's inequality to the random variables |X |r and 1Ω, we obtain

In particular, if the sth absolute moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
is finite, then the r th absolute moment is finite, too. (This also follows from Jensen's inequality
Jensen's inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...
.)
Product measure
For two σ-finite measure spaces and define the product measure space by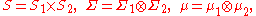
where S is the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of S1 and S2, the σ-algebra Σ arises as product σ-algebra of Σ1 and Σ2, and μ denotes the product measure
Product measure
In mathematics, given two measurable spaces and measures on them, one can obtain the product measurable space and the product measure on that space...
of μ1 and μ2. Then Tonelli's theorem allows us to rewrite Hölder's inequality using iterated integrals: If f and g are real- or complex-valued functions on the Cartesian product S, then

This can be generalized to more than two σ-finite measure spaces.
Vector-valued functions
Let denote a σ-finite measure space and suppose that and are functions on S, taking values in the n-dimensional real- or complex Euclidean space. By taking the product with the counting measure on }, we can rewrite the above product measure version of Hölder's inequality in the form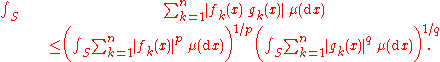
This generalizes to functions f and g taking values in a sequence space
Sequence space
In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...
.
Proof of Hölder's inequality
There are several proofs of Hölder's inequality; the main idea in the following is Young's inequalityYoung's inequality
In mathematics, the term Young's inequality is used for two inequalities: one about the product of two numbers, and one about the convolution of two functions. They are named for William Henry Young....
.
If ||f ||p = 0, then f is zero μ-almost everywhere, and the product fg is zero μ-almost everywhere, hence the left-hand side of Hölder's inequality is zero. The same is true if ||g ||q = 0. Therefore, we may assume ||f ||p > 0 and ||g ||q > 0 in the following.
If ||f ||p = ∞ or ||g ||q = ∞, then the right-hand side of Hölder's inequality is infinite. Therefore, we may assume that ||f ||p and ||g ||q are in (0, ∞).
If p = ∞ and q = 1, then |fg | ≤ ||f ||∞ |g | almost everywhere and Hölders inequality follows from the monotonicity of the Lebesgue integral. Similarly for p = 1 and q = ∞. Therefore, we may also assume p, q ∈ (1, ∞).
Dividing f and g by ||f ||p and ||g ||q, respectively, we can assume that
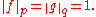
We now use Young's inequality, which states that
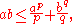
for all nonnegative a and b, where equality is achieved if and only if a p = b q. Hence
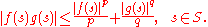
Integrating both sides gives
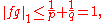
which proves the claim.
Under the assumptions p ∈ (1, ∞) and ||f ||p = ||g ||q = 1, equality holds if and only if |f |p = |g |q almost everywhere. More generally, if ||f ||p and ||g ||q are in (0, ∞), then Hölder's inequality becomes an equality if and only if there exist real numbers α, β > 0, namely
 and
and 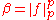
such that
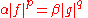 μ-almost everywhere (*)
μ-almost everywhere (*)The case ||f ||p = 0 corresponds to β = 0 in (*). The case ||g ||q = 0 corresponds to α = 0 in (*).
Statement
Assume that 1 ≤ p < ∞ and let q denote the Hölder conjugate. Then, for every ƒ ∈ Lp(μ),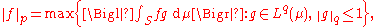
where max indicates that there actually is a g maximizing the right-hand side. When p = ∞ and if each set A in the σ-field Σ with μ(A) = ∞ contains a subset B ∈ Σ with 0 < μ(B) < ∞ (which is true in particular when μ is σ-finite), then
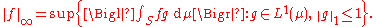
Remarks and examples
- The equality for p = ∞ fails whenever there exists a set A in the σ-field Σ with μ(A) = ∞ that has no subset B ∈ Σ with 0 < μ(B) < ∞ (the simplest example is the σ-field Σ containing just the empty set and S, and the measure μ with μ(S) = ∞). Then the indicator function 1A satisfies ||1A||∞ = 1, but every g ∈ L1(μ) has to be μ-almost everywhere constant on A, because it is Σ-measurable, and this constant has to be zero, because g is μ-integrable. Therefore, the above supremum for the indicator function 1A is zero and the extremal equality fails.
- For p = ∞, the supremum is in general not attained. As an example, let S denote the natural numbers (without zero), Σ the power set of S, and μ the counting measure. Define ƒ(n) = (n − 1)/n for every natural number n. Then ||ƒ ||∞ = 1. For g ∈ L1(μ) with 0 < ||g ||1 ≤ 1, let m denote the smallest natural number with g(m) ≠ 0. Then
Applications
- The extremal equality is one of the ways for proving the triangle inequality ||ƒ1 + ƒ2||p ≤ ||ƒ1||p + ||ƒ2||p for all ƒ1 and ƒ2 in Lp(μ), see Minkowski inequalityMinkowski inequalityIn mathematical analysis, the Minkowski inequality establishes that the Lp spaces are normed vector spaces. Let S be a measure space, let 1 ≤ p ≤ ∞ and let f and g be elements of Lp...
.
- Hölder's inequality implies that every ƒ ∈ Lp(μ) defines a bounded (or continuous) linear functional κƒ on Lq(μ) by the formula
-
- The extremal equality (when true) shows that the norm of this functional κƒ as element of the continuous dual space Lq(μ)∗ coincides with the norm of ƒ in Lp(μ) (see also the Lp-space article).
Generalization of Hölder's inequality
Assume that r ∈ (0, ∞) and p1, …, pn ∈ (0, ∞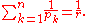
Then, for all measurable real- or complex-valued functions f1, …, fn defined on S,
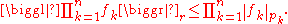
In particular,
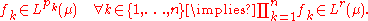
Note:
- For r ∈ (0, 1), contrary to the notation, ||.||r is in general not a norm, because it doesn't satisfy the triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
.
Interpolation
Let p1, …, pn ∈ (0, ∞Harmonic mean
In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
, i.e.,
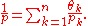
Given a measurable real- or complex-valued functions f on S, define
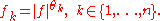
Then by the above generalization of Hölder's inequality,
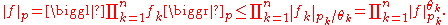
As an interpolation
Riesz-Thorin theorem
In mathematics, the Riesz–Thorin theorem, often referred to as the Riesz–Thorin interpolation theorem or the Riesz–Thorin convexity theorem is a result about interpolation of operators. It is named after Marcel Riesz and his student G. Olof Thorin.This theorem bounds the norms of linear maps...
result for n = 2,

where θ ∈ (0, 1) and
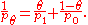
Reverse Hölder inequality
Assume that p ∈ (1, ∞) and that the measure space (S, Σ, μ) satisfies μ(S) > 0. Then, for all measurable real- or complex-valued functions f and g on S such that g(s) ≠ 0 for μ-almost all s ∈ S,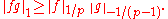
If ||fg ||1 < ∞ and ||g ||−1/(p −1) > 0, then the reverse Hölder inequality is an equality if and only if there exists an α ≥ 0 such that
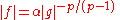 μ-almost everywhere.
μ-almost everywhere.Note: ||f ||1/p and ||g ||−1/(p −1) are not norms, these expressions are just compact notation for
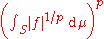 and
and 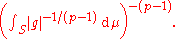
Conditional Hölder inequality
Let be a probability space,
be a probability space,  a sub-σ-algebra, and p, q ∈ (1, ∞) Hölder conjugates, meaning that 1/p + 1/q = 1. Then, for all real- or complex-valued random variables X and Y on Ω,
a sub-σ-algebra, and p, q ∈ (1, ∞) Hölder conjugates, meaning that 1/p + 1/q = 1. Then, for all real- or complex-valued random variables X and Y on Ω,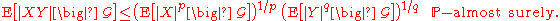
Remarks:
- If a non-negative random variable Z has infinite expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
, then its conditional expectationConditional expectationIn probability theory, a conditional expectation is the expected value of a real random variable with respect to a conditional probability distribution....
is defined by
- On the right-hand side of the conditional Hölder inequality, 0 times ∞ as well as ∞ times 0 means 0. Multiplying a > 0 with ∞ gives ∞.