Conditional expectation - AbsoluteAstronomy.com

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

, a conditional expectation (also known as conditional expected value or conditional mean) is the expected value

Expected value

In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...

of a real random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

with respect to a conditional probability distribution.

The concept of conditional expectation is extremely important in Kolmogorov

Andrey Kolmogorov

Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...

's measure-theoretic definition of probability theory

Probability theory

. In fact, the concept of conditional probability itself is actually defined in terms of conditional expectation.

Introduction

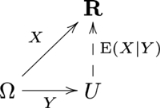
Let X and Y be discrete random variables, then the conditional expectation of X given the event Y=y is a function of y over the range of Y

where

is the range

Range (mathematics)

In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...

of X.

A problem arises when we attempt to extend this to the case where Y is a continuous random variable. In this case, the probability P(Y=y) = 0, and the Borel–Kolmogorov paradox demonstrates the ambiguity of attempting to define conditional probability along these lines.

However the above expression may be rearranged:

and although this is trivial for individual values of y (since both sides are zero), it should hold for any measurable subset B of the domain of Y that:

In fact, this is a sufficient condition to define both conditional expectation, and conditional probability.

Formal definition

Let

be a probability space

Probability space

In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...

, with a real random variable X and a sub-σ-algebra

Sigma-algebra

In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...

. Then a conditional expectation of X given

is any

-measurable function

Measurable function

In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...

which satisfies:

.

Note that

is simply the name of the conditional expectation function.

Discussion

A couple of points worth noting about the definition:

This is not a constructive definition; we are merely given the required property that a conditional expectation must satisfy.
- The required property has the same form as the last expression in the Introduction section.
- Existence of a conditional expectation function is determined by the Radon–Nikodym theorem
  Radon–Nikodym theorem
  In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
  
  , a sufficient condition is that the (unconditional) expected value for X exist.
- Uniqueness can be shown to be almost sure
  Almost surely
  In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
  
  : that is, versions of the same conditional expectation will only differ on a set of probability zero
  Null set
  In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
  
  .
The σ-algebra controls the "granularity" of the conditioning. A conditional expectation over a finer-grained σ-algebra will allow us to condition on a wider variety of events.
- To condition freely on values of a random variable Y with state space , it suffices to define the conditional expectation using the pre-image of Σ with respect to Y:

This suffices to ensure that the conditional expectation is σ(Y)-measurable. Although conditional expectation is defined to condition on events in the underlying probability space Ω, the requirement that it be σ(Y)-measurable allows us to condition on

as in the introduction.

Definition of conditional probability

For any event

, define the indicator function:

which is a random variable with respect to the Borel σ-algebra

Borel algebra

In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...

on (0,1). Note that the expectation of this random variable is equal to the probability of A itself:

Then the conditional probability

Conditional probability

In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...

given

is a function

such that

is the conditional expectation of the indicator function for A:

In other words,

is a

-measurable function satisfying

A conditional probability is regular if

is also a probability measure

Probability measure

In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...

for all ω ∈ Ω. An expectation of a random variable with respect to a regular conditional probability is equal to its conditional expectation.

For the trivial sigma algebra the conditional probability is a constant function,

For , as outlined above, .

Conditioning as factorization

In the definition of conditional expectation that we provided above, the fact that Y is a real random variable is irrelevant: Let U be a measurable space, that is, a set equipped with a σ-algebra

of subsets. A U-valued random variable is a function

such that

for any measurable subset

of U.

We consider the measure Q on U given as above: Q(B) = P(Y⁻¹(B)) for every measurable subset B of U. Then Q is a probability measure on the measurable space U defined on its σ-algebra of measurable sets.

Theorem. If X is an integrable random variable on Ω then there is one and, up to equivalence a.e. relative to Q, only one integrable function g on U (which is written

) such that for any measurable subset B of U:

There are a number of ways of proving this; one as suggested above, is to note that the expression on the left hand side defines, as a function of the set B, a countably additive signed measure μ on the measurable subsets of U. Moreover, this measure μ is absolutely continuous relative to Q. Indeed Q(B) = 0 means exactly that Y⁻¹(B) has probability 0. The integral of an integrable function on a set of probability 0 is itself 0. This proves absolute continuity. Then the Radon–Nikodym theorem

Radon–Nikodym theorem

In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...

provides the function g, equal to the density of μ with respect to Q.

The defining condition of conditional expectation then is the equation

and it holds that

We can further interpret this equality by considering the abstract change of variables

Change of variables

In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with new ones; the new and old variables being related in some specified way...

formula to transport the integral on the right hand side to an integral over Ω:

This equation can be interpreted to say that the following diagram is commutative

Commutative diagram

In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...

in the average.
E(X|Y)= goY
Ω ───────────────────────────> R
Y g=E(X|Y= ·)
Ω ──────────> R ───────────> R

ω ──────────> Y(ω) ───────────> g(Y(ω)) = E(X|Y=Y(ω))

y ───────────> g( y ) = E(X|Y= y )

The equation means that the integrals of X and the composition

over sets of the form Y⁻¹(B), for B a measurable subset of U, are identical.

Conditioning relative to a subalgebra

There is another viewpoint for conditioning involving σ-subalgebras N of the σ-algebra M. This version is a trivial specialization of the preceding: we simply take U to be the space Ω with the σ-algebra N and Y the identity map. We state the result:

Theorem. If X is an integrable real random variable on Ω then there is one and, up to equivalence a.e. relative to P, only one integrable function g such that for any set B belonging to the subalgebra N

where g is measurable with respect to N (a stricter condition than the measurability with
respect to M required of X).
This form of conditional expectation is usually written: E(X|N).
This version is preferred by probabilists. One reason is that on the space of square-integrable real random variables (in other words, real random variables with finite second moment) the mapping X → E(X|N)
is self-adjoint

and an orthogonal projection

Basic properties

Let (Ω, M, P) be a probability space, and let N be a σ-subalgebra of M.

Conditioning with respect to N is linear on the space of integrable real random variables.

More generally, for every integrable N–measurable random variable Y on Ω.

for all B ∈ N and every integrable random variable X on Ω.

Jensen's inequality
Jensen's inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...

holds: If ƒ is a convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...

, then

Conditioning is a contractive projection

for any s ≥ 1.