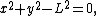
Holonomic
Encyclopedia
In mathematics
and physics
, the term holonomic may occur with several different meanings.
is a set of basis vectors ek for which all Lie derivative
s vanish:
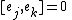
Some authors call a holonomic basis a coordinate basis, and a nonholonomic basis a non-coordinate basis. See also Jet bundle
.
a system may be defined as holonomic if all constraints of the system are holonomic. For a constraint to be holonomic it must be expressible as a function
:
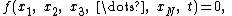
i.e. a holonomic constraint depends only on the coordinates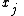
and time 
. It does not depend on the velocities. A constraint that cannot be expressed in the form shown above is a nonholonomic constraint
.
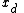which is a parameter in the constraint equation 
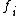, we can rearrange the equation into the following form, assuming it can be done,
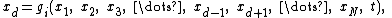
and replace the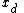
in every equation of the system using the above function. This can always be done for general physical system, provided that 
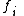is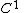 
, then by implicit function theorem
, the solution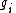
is guaranteed in some open set. Thus, it is possible to remove all occurrences of the dependent variable 
.
Suppose that a physical system has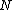
degrees of freedom. Now, 
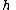holonomic constraints are imposed on the system. Then, the number of degrees of freedom is reduced to 
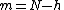. We can use 
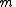independent generalized coordinates (
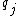) to completely describe the motion of the system. The transformation equation can be expressed as follows:
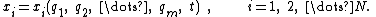
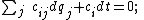
where cij, ci are the coefficients of the differentials dqj and dt for the ith constraint.
If the differential form is integrable, i.e., if there is a function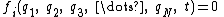
satisfying the equality
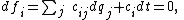
then, this constraint is a holonomic constraint; otherwise, nonholonomic. Therefore, all holonomic and some nonholonomic constraints can be expressed using the differential form. Not all nonholonomic constraints can be expressed this way. Examples of nonholonomic constraints which can not be expressed this way are those that are dependent on generalized velocities. With constraint equation in differential form, whether a constraint is holonomic or nonholonomic depends on the integrability of the differential form.
, then Hamilton's principle
is the necessary and sufficient condition for the correctness of Lagrange's equation.
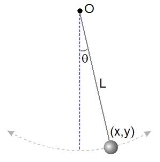
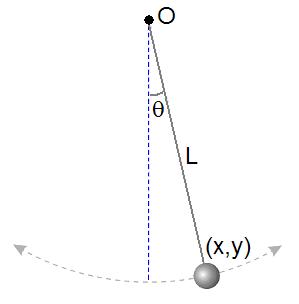As shown at right, a simple pendulum
is a system composed of a weight and a string. The string is attached at the top end to a pivot and at the bottom end to a weight. Being inextensible, the string’s length is a constant. Therefore, this system is holonomic; it obeys holonomic constraint
where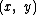
is the position of the weight and 
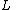is length of the string.
The particles of a rigid body
obey the holonomic constraint
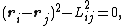
where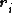
, 
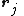are respectively the positions of particles 
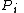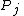and 
, and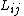
is the distance between them.
school of D-module
theory, holonomic system has a further, technical meaning. Roughly speaking, with a D-module considered as a system of partial differential equation
s on a manifold
, a holonomic system is a highly over-determined system, such that the solutions locally form a vector space of finite dimension (instead of the expected dependence on some arbitrary function). Such systems have been applied, for example, to the Riemann–Hilbert problem in higher dimensions, and to quantum field theory
.
with polynomial coefficients. A function defined on the natural number
s is holonomic if it satisfies a linear homogenous recurrence relation
(or equivalently, a linear homogenous difference equation) with polynomial coefficients. The two concepts are closely related: a function represented by a power series is holonomic if and only if the coefficients are holonomic. A holonomic function on the natural numbers is also called P-recursive.
Examples of holonomic functions are exp, ln, sin, cos, arcsin, arccos, xa, with many more. Not all elementary functions are holonomic, for example the tangent and secant are not. Holonomic functions are closed under sum, product and right composition with algebraic functions, but not division.
, holonomicity refers to the relationship between the controllable and total degrees of freedom
of a given robot
(or part thereof). If the controllable degrees of freedom is equal to the total degrees of freedom then the robot is said to be holonomic. If the controllable degrees of freedom are less than the total degrees of freedom it is non-holonomic. A robot is considered to be redundant
if it has more controllable degrees of freedom than degrees of freedom in its task space. Holonomicity can be used to describe simple objects as well.
An automobile
is an example of a non-holonomic vehicle. The vehicle has three degrees of freedom—its position in two axes, and its orientation relative to a fixed heading. Yet it has only two controllable degrees of freedom—acceleration
/braking
and the angle of the steering wheel
—with which to control its position and orientation. A car's heading (the direction in which it is traveling) must remain aligned with the orientation of the car, or 180° from it if the car is in reverse. It has no other allowable direction, assuming there is no skidding or sliding. Thus, not every path in phase space is achievable; however, every path can be approximated by a holonomic path – this is called a (dense) homotopy principle. The non-holonomicity of a car makes parallel parking
and turning in the road
difficult, but the homotopy principle says that these are always possible, assuming that clearance exists.
Holonomic forms of locomotion, such as that used by Ballbot
, allow vehicles to immediately move in any direction without needing to turn first.
A human arm, by contrast, is a holonomic, redundant system because it has seven degrees of freedom (three in the shoulder - rotations about each axis, two in the elbow - bending and rotation about the lower arm axis, and two in the wrist, bending up and down (i.e. pitch), and left and right (i.e. yaw)) and there are only six physical degrees of freedom in the task of placing the hand (x, y, z, roll, pitch and yaw), while fixing the seven degrees of freedom fixes the hand. See also sub-Riemannian geometry for a discussion of holonomic constraints in robotics.
and David Bohm
, models cognitive function as being guided by a matrix of neurological wave interference patterns. This model has important implications in neurology
, especially in the field of human memory.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the term holonomic may occur with several different meanings.
Holonomic basis
A holonomic basis for a manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is a set of basis vectors ek for which all Lie derivative
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
s vanish:
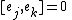
Some authors call a holonomic basis a coordinate basis, and a nonholonomic basis a non-coordinate basis. See also Jet bundle
Jet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
.
Holonomic system (physics)
In classical mechanicsClassical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
a system may be defined as holonomic if all constraints of the system are holonomic. For a constraint to be holonomic it must be expressible as a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
:
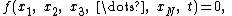
i.e. a holonomic constraint depends only on the coordinates
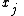and time . It does not depend on the velocities. A constraint that cannot be expressed in the form shown above is a nonholonomic constraintNonholonomic system
A nonholonomic system in physics and mathematics is a system whose state depends on the path taken to achieve it. Such a system is described by a set of parameters subject to differential constraints, such that when the system evolves along a path in its parameter space but finally returns to the...
.
Transformation to general coordinates
The holonomic constraint equations can help us easily remove some of the dependent variables in our system. For example, if we want to remove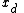 which is a parameter in the constraint equation 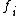, we can rearrange the equation into the following form, assuming it can be done,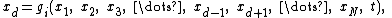and replace the
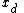in every equation of the system using the above function. This can always be done for general physical system, provided that 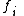is 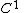, then by implicit function theoremImplicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
, the solution
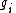is guaranteed in some open set. Thus, it is possible to remove all occurrences of the dependent variable .Suppose that a physical system has
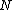degrees of freedom. Now, 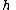holonomic constraints are imposed on the system. Then, the number of degrees of freedom is reduced to 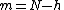. We can use 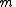independent generalized coordinates (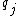) to completely describe the motion of the system. The transformation equation can be expressed as follows: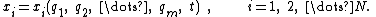Differential form
Consider the following differential form of a constraint equation: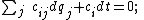where cij, ci are the coefficients of the differentials dqj and dt for the ith constraint.
If the differential form is integrable, i.e., if there is a function
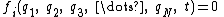satisfying the equality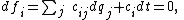then, this constraint is a holonomic constraint; otherwise, nonholonomic. Therefore, all holonomic and some nonholonomic constraints can be expressed using the differential form. Not all nonholonomic constraints can be expressed this way. Examples of nonholonomic constraints which can not be expressed this way are those that are dependent on generalized velocities. With constraint equation in differential form, whether a constraint is holonomic or nonholonomic depends on the integrability of the differential form.
Classification of physical systems
In order to study classical physics rigorously and methodically, we need to classify systems. Based on previous discussion, we can classify physical systems into holonomic systems and non-holonomic systems. One of the conditions for the applicability of many theorems and equations is that the system must be a holonomic system. For example, if a physical system is a holonomic system and a monogenic systemMonogenic system
In physics, among the most studied physical systems in classical mechanics are monogenic systems. A monogenic system has excellent mathematical characteristics and is very well suited for mathematical analysis...
, then Hamilton's principle
Hamilton's principle
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...
is the necessary and sufficient condition for the correctness of Lagrange's equation.
Examples
Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
is a system composed of a weight and a string. The string is attached at the top end to a pivot and at the bottom end to a weight. Being inextensible, the string’s length is a constant. Therefore, this system is holonomic; it obeys holonomic constraint
where
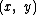is the position of the weight and 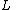is length of the string.The particles of a rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
obey the holonomic constraint
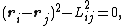
where
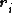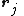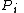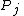, are respectively the positions of particles and , and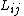 is the distance between them.Holonomic system (D-modules)
In the Mikio SatoMikio Sato
is a Japanese mathematician, who started the field of algebraic analysis. He studied at the University of Tokyo, and then did graduate study in physics as a student of Shin'ichiro Tomonaga...
school of D-module
D-module
In mathematics, a D-module is a module over a ring D of differential operators. The major interest of such D-modules is as an approach to the theory of linear partial differential equations...
theory, holonomic system has a further, technical meaning. Roughly speaking, with a D-module considered as a system of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s on a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, a holonomic system is a highly over-determined system, such that the solutions locally form a vector space of finite dimension (instead of the expected dependence on some arbitrary function). Such systems have been applied, for example, to the Riemann–Hilbert problem in higher dimensions, and to quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
Holonomic function
A smooth function in one variable is holonomic if it satisfies a linear homogenous differential equationLinear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
with polynomial coefficients. A function defined on the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s is holonomic if it satisfies a linear homogenous recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
(or equivalently, a linear homogenous difference equation) with polynomial coefficients. The two concepts are closely related: a function represented by a power series is holonomic if and only if the coefficients are holonomic. A holonomic function on the natural numbers is also called P-recursive.
Examples of holonomic functions are exp, ln, sin, cos, arcsin, arccos, xa, with many more. Not all elementary functions are holonomic, for example the tangent and secant are not. Holonomic functions are closed under sum, product and right composition with algebraic functions, but not division.
Robotics
In roboticsRobotics
Robotics is the branch of technology that deals with the design, construction, operation, structural disposition, manufacture and application of robots...
, holonomicity refers to the relationship between the controllable and total degrees of freedom
Degrees of freedom (engineering)
In mechanics, degrees of freedom are the set of independent displacements and/or rotations that specify completely the displaced or deformed position and orientation of the body or system...
of a given robot
Robot
A robot is a mechanical or virtual intelligent agent that can perform tasks automatically or with guidance, typically by remote control. In practice a robot is usually an electro-mechanical machine that is guided by computer and electronic programming. Robots can be autonomous, semi-autonomous or...
(or part thereof). If the controllable degrees of freedom is equal to the total degrees of freedom then the robot is said to be holonomic. If the controllable degrees of freedom are less than the total degrees of freedom it is non-holonomic. A robot is considered to be redundant
Redundancy (total quality management)
In total quality management, TQM, redundancy in quality or redundant quality means quality which exceeds the required quality level. Tolerances may be too accurate, for example, creating unnecessarily high costs of production....
if it has more controllable degrees of freedom than degrees of freedom in its task space. Holonomicity can be used to describe simple objects as well.
An automobile
Automobile
An automobile, autocar, motor car or car is a wheeled motor vehicle used for transporting passengers, which also carries its own engine or motor...
is an example of a non-holonomic vehicle. The vehicle has three degrees of freedom—its position in two axes, and its orientation relative to a fixed heading. Yet it has only two controllable degrees of freedom—acceleration
Throttle
A throttle is the mechanism by which the flow of a fluid is managed by constriction or obstruction. An engine's power can be increased or decreased by the restriction of inlet gases , but usually decreased. The term throttle has come to refer, informally and incorrectly, to any mechanism by which...
/braking
Brake
A brake is a mechanical device which inhibits motion. Its opposite component is a clutch. The rest of this article is dedicated to various types of vehicular brakes....
and the angle of the steering wheel
Steering wheel
A steering wheel is a type of steering control in vehicles and vessels ....
—with which to control its position and orientation. A car's heading (the direction in which it is traveling) must remain aligned with the orientation of the car, or 180° from it if the car is in reverse. It has no other allowable direction, assuming there is no skidding or sliding. Thus, not every path in phase space is achievable; however, every path can be approximated by a holonomic path – this is called a (dense) homotopy principle. The non-holonomicity of a car makes parallel parking
Parallel parking
thumb|250px|right|Parallel-parked cars in [[Washington, D.C.]]thumb|250px|right|A motorist gets assistance parallel-parkingParallel parking is a method of parking a vehicle in line with other parked cars. Cars parked in parallel are in one line, parallel to the curb, with the front bumper of each...
and turning in the road
Turning in the road
In driving unarticulated wheeled vehicles with reversible propulsion systems, turning in the road is a category of maneuvers, each reversing a vehicle's direction of travel along a road, with neither the use of any intersections nor leaving the right-of-way....
difficult, but the homotopy principle says that these are always possible, assuming that clearance exists.
Holonomic forms of locomotion, such as that used by Ballbot
Ballbot
A Ballbot is a mobile robot designed to balance itself on a single spherical wheel , both while in motion or staying in place. Through its single contact point with the ground, a Ballbot is omnidirectional and thus exceptionally agile, maneuverable and organic in motion compared to other ground...
, allow vehicles to immediately move in any direction without needing to turn first.
A human arm, by contrast, is a holonomic, redundant system because it has seven degrees of freedom (three in the shoulder - rotations about each axis, two in the elbow - bending and rotation about the lower arm axis, and two in the wrist, bending up and down (i.e. pitch), and left and right (i.e. yaw)) and there are only six physical degrees of freedom in the task of placing the hand (x, y, z, roll, pitch and yaw), while fixing the seven degrees of freedom fixes the hand. See also sub-Riemannian geometry for a discussion of holonomic constraints in robotics.
Holonomic brain theory
Holonomic brain theory, developed by Karl PribramKarl H. Pribram
Karl H. Pribram is a professor at Georgetown University, in the United States, and an emeritus professor of psychology and psychiatry at Stanford University and Radford University...
and David Bohm
David Bohm
David Joseph Bohm FRS was an American-born British quantum physicist who contributed to theoretical physics, philosophy, neuropsychology, and the Manhattan Project.-Youth and college:...
, models cognitive function as being guided by a matrix of neurological wave interference patterns. This model has important implications in neurology
Neurology
Neurology is a medical specialty dealing with disorders of the nervous system. Specifically, it deals with the diagnosis and treatment of all categories of disease involving the central, peripheral, and autonomic nervous systems, including their coverings, blood vessels, and all effector tissue,...
, especially in the field of human memory.