Monogenic system
Encyclopedia
In physics
, among the most studied physical systems in classical mechanics
are monogenic systems. A monogenic system has excellent mathematical characteristics and is very well suited for mathematical analysis. It is considered a logical starting point for any serious physics endeavour.
In a physical system, if all forces, with the exception of the constraint forces, are derivable from the generalized scalar potential, and this generalized scalar potential is a function of generalized coordinates, generalized velocities, or time, then, this system is a monogenic system.
Expressed using equations, the exact relationship between generalized force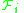
and generalized potential 
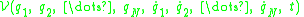is as follows:
where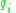
is generalized coordinate, 
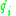is generalized velocity, and 
is time.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, among the most studied physical systems in classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
are monogenic systems. A monogenic system has excellent mathematical characteristics and is very well suited for mathematical analysis. It is considered a logical starting point for any serious physics endeavour.
In a physical system, if all forces, with the exception of the constraint forces, are derivable from the generalized scalar potential, and this generalized scalar potential is a function of generalized coordinates, generalized velocities, or time, then, this system is a monogenic system.
Expressed using equations, the exact relationship between generalized force
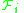and generalized potential 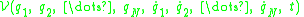is as follows:where
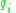is generalized coordinate, 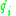is generalized velocity, and is time.- If the generalized potential in a monogenic system depends only on generalized coordinates, and not on generalized velocities and time, then, this system is a conservative systemConservative forceA conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...
.The relationship between generalized force and generalized potential is as follows:
-
；
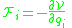- Lagrangian mechanicsLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
often involves monogenic systems. If a physical system is both a holonomicHolonomicIn mathematics and physics, the term holonomic may occur with several different meanings.-Holonomic basis:A holonomic basis for a manifold is a set of basis vectors ek for which all Lie derivatives vanish:[e_j,e_k]=0 \,...
system and a monogenic system, then it’s possible to derive Lagrange's equationLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
s from d'Alembert's principleD'Alembert's principleD'Alembert's principle, also known as the Lagrange–d'Alembert principle, is a statement of the fundamental classical laws of motion. It is named after its discoverer, the French physicist and mathematician Jean le Rond d'Alembert...
; it's also possible to derive Lagrange's equationLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
s from Hamilton's principleHamilton's principleIn physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...
.